Современное понимание рекурсии: определение функциональности и обращения к ней извне и из этой функциональности. Считается, что рекурсия была рождена математиками: вычисление факториала, бесконечные ряды, фракталы, непрерывные дроби... Однако, рекурсию можно обнаружить везде. Объективные природные законы «считают» рекурсию своим основным алгоритмом и формой выражения (существования) не столько предметов материального мира, сколько вообще основным алгоритмом движения.

Люди различных специальностей в различных областях науки и техники используют рекурсивный алгоритм f (x), где «x ~/= f (x)». Функция, вызывающая сама себя, - сильное решение, но формирование и понимание этого решения, в большинстве случаев, очень непростая задача.
В далекие времена применяли рекурсию для увеличения дворцового пространства. Через систему направленных друг на друга зеркал, можно создать потрясающие объемные пространственные эффекты. Но так ли легко понять, как настроить эти зеркала? А еще более сложно определить, где находится точка в пространстве, отраженная через несколько зеркал.
Рекурсия, рекурсивные алгоритмы: смысл и синтаксис
Задача, которая формулируется повторением последовательности операций может быть решена рекурсивно. Простой алгоритм (вычисление квадратного уравнения, скрипт наполнения веб-страницы информацией, чтение файла, передача сообщения...) не требует применения рекурсии.
Основные отличия алгоритма, который допускает рекурсивное решение:
- есть алгоритм, который нужно выполнить несколько раз;
- алгоритм нуждается в данных, которые изменяются каждый раз;
- алгоритм не обязательно должен изменяться каждый раз;
- есть финальное условие: алгоритм рекурсивный - не бесконечен.
В общем случае, нельзя утверждать, что однократность исполнения - обязательное условие отсутствия повода для рекурсии. Нельзя также требовать наличия обязательного финального условия: у бесконечных рекурсий есть своя сфера применения.
Алгоритм рекурсивный: когда последовательность операций выполняется многократно, на данных, которые изменяются каждый раз и дающий каждый раз новый результат.
Формула рекурсии
Математическое понимание рекурсии и её аналог в программировании отличны. Математике хоть и свойственны признаки программирования, но программирование - это математика гораздо более высокого порядка.

Хорошо написанный алгоритм - как зеркало интеллекта его автора. Общая формула рекурсии в программировании «f (x)», где «x ~/= f (x)» имеет, как минимум, два варианта интерпретации. Здесь «~» - подобие или отсутствие результата, а «=» - наличие результата функции.
Первый вариант: динамика данных.
- функция «f(x)» имеет алгоритм рекурсивный и не изменяемый;
- «x» и результат «f(x)» - каждый раз имеют новые значения, результат «f(x)» является новым параметром «x» этой функции.
Второй вариант: динамика кода.
- функция «f(x)» имеет несколько алгоритмов, уточняющих (анализирующих) данные;
- анализ данных - одна часть кода и реализация рекурсивных алгоритмов, выполняющих нужное действие, - вторая часть кода;
- результата функции «f(x)» - нет.
Отсутствие результата - нормальное явление. Программирование - это не математика, здесь результат не обязательно должен присутствовать явно. Функция, исполняемая рекурсивно, может просто делать парсинг сайтов и наполнять базу данных, или создавать нужные экземпляры объектов согласно поступающему входному потоку.
Данные и рекурсия
Программирование рекурсивных алгоритмов - это не вычисление факториала, в котором функция получает каждый раз данное, отличное на единицу в меньшую или большую сторону - вариант реализации зависит от предпочтения разработчика.
Не суть важно, как считать факториал «8!», двигаясь от 0, 1, 2, ... или наоборот 8, 7, 6 ... Аналогично вычисление математической последовательности, фрактала или бесконечного ряда записывается простой математической формулой и, соответственно, алгоритмом, который строго следует этой формуле.
Обработка информации - это «математика» совершенно другого порядка. Рекурсивные функции и алгоритмы здесь оперируют буквами, словами, фразами, предложениями и абзацами. Каждый следующий уровень использует предыдущий.
Входной поток данных анализируется по широкому спектру условий, но процесс анализа в целом рекурсивен. Нет смысла писать уникальные алгоритмы на все варианты входного потока. Должен быть один функционал. Здесь рекурсивные алгоритмы примеры того, как сформировать выходной поток, адекватный входному. Это не результат, поступающий на вход рекурсивного алгоритма, но это желаемое и необходимое решение.
Абстракция, рекурсия и ООП
Объектно-ориентированное программирование (ООП) и рекурсия - кардинально разные сущности, но они идеально дополняют друг друга. Абстракция не имеет никакого отношения к рекурсии, но сквозь призму ООП создает возможность реализации контекстной рекурсии.
Например, идет разбор информации и выделяются отдельно буквы, слова, фразы, предложения и абзацы. Очевидно, разработчик предусмотрит создание экземпляров объектов этих пяти типов и предложит решение рекурсивных алгоритмов на каждом уровне.

Между тем, если на уровне букв «нет смысла искать смысл», то на уровне слов появляется семантика. Можно разделить слова на глаголы, существительные, наречия, предлоги ... Можно пойти дальше и определить падежи.
На уровне фраз семантика дополняется знаками пунктуации и логикой сочетания слов. На уровне предложений обнаруживается более совершенный уровень семантики, а абзац можно рассматривать, как законченную мысль.
Объектно-ориентированная разработка предопределяет наследование свойств и методов и предлагает начинать иерархию объектов с создания абсолютно абстрактного предка. При этом, вне всякого сомнения, анализ каждого потомка будет иметь рекурсивный характер и не слишком отличаться на техническом уровне по многим позициям (буквы, слова, фразы и предложения). Абзацы, как законченные мысли, могут выделяться из этого списка, но не суть.
Важно, что подавляющую часть алгоритма можно сформулировать на уровне абстрактного предка, уточняя её на уровне каждого потомка данными и методами, вызываемыми с абстрактного уровня. В данном контексте абстракция открывает новые горизонты для рекурсии.
Исторические особенности ООП
ООП приходило в мир программ дважды, хотя некоторые специалисты могут выделить появление облачных технологий и современные представления об объектах и классах, как новый виток в развитии ИТ-технологий.
Термины «объект» и «объектный» в современном контексте ООП, принято относить к 50-м и 60-м годам прошлого века, но ассоциировать их с 1965 годом и появлением языков Simula, Lisp, Algol, Smalltalk.
В те времена программирование не отличалось особым развитием и не могло адекватно реагировать на революционные концепции. До борьбы идей и стилей программирования (С/С++ и Pascal - в основном) еще было далеко, а базы данных еще только формировались концептуально.

В конце 80-х и начале 90-х в Pascal появились объекты и все вспомнили про классы в С/С++ - это ознаменовало новый виток интереса к ООП и именно тогда инструментальные средства, прежде всего языки программирования стали не только поддерживать объектно-ориентированные идеи, но и развиваться соответственно им.
Естественно, если раньше рекурсивные алгоритмы представляли собой просто функции, используемые в общем коде программы, то теперь рекурсия могла стать частью свойств объекта (класса), что в контексте наследования предоставляло интересные возможности.
Особенность современного ООП
Развитие ООП изначально декларировало объекты (классы) как совокупности данных и свойств (методов). Фактически речь шла о данных, имеющих синтаксис и смысл. Но тогда не удалось представить ООП, как инструмент управления реальными объектами.
ООП превратилось в инструмент управления объектами «компьютерной природы». Скрипт, кнопка, элемент меню, строка меню, тег в окне браузера - это объект. Но не станок, продукт питания, слово, или предложение. Реальные объекты остались за пределами объектно-ориентированного программирования, а компьютерные инструменты приобрели новое воплощение.
Вследствие отличий популярных языков программирования, появилось множество диалектов ООП. По семантике они практически эквивалентны, а их ориентация на инструментальную сферу, а не на прикладную, делает возможным выносить описание реальных объектов за пределы алгоритмов и обеспечивать их межплатформенное и межъязыковое «существование».
Стеки и механизмы вызова функций
Механизмы вызова функций (процедур, алгоритмов) требуют передачи данных (параметров), возврат результата и запоминание адреса оператора, который должен получить управление после завершения функции (процедуры).
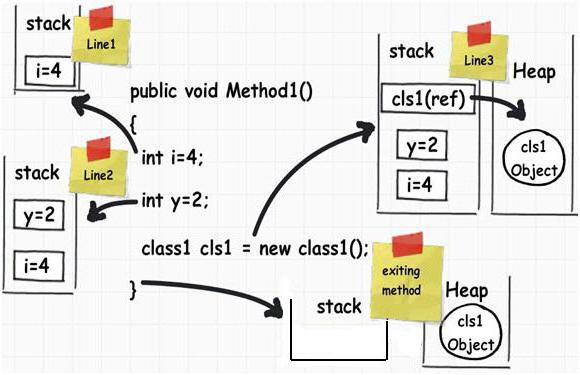
Обычно для этих целей используется стек, хотя языки программирования или сам программист-разработчик может предусмотреть самые разнообразные варианты передачи управления. Современное программирование допускает, что имя функции может быть не только параметром: оно может формироваться в процессе исполнения алгоритма. Алгоритм также может быть создан в процессе исполнения другого алгоритма.
Понятие рекурсивных алгоритмов, когда их имена и тела могут быть определены в момент образования задачи (выбора нужного алгоритма) расширяет рекурсивность не только на то, как что-то сделать, но и кто именно это должен сделать. Выбор алгоритма по его «осмысленному» имени - перспективно, но создает трудности.
Рекурсивность на множестве функций
Нельзя сказать, что алгоритм рекурсивный, когда он вызывает себя и только. Программирование - не догма, а понятие рекурсивности - это не исключительное требование вызывать себя из тела собственного алгоритма.
Практические области применения не всегда дают чистое решение. Часто исходные данные следует готовить, а результат рекурсивного вызова необходимо анализировать в контексте всей задачи (всего алгоритма) в целом.
Фактически, не только перед вызовом рекурсивной функции, но и после её завершения, может или должна быть вызвана другая программа. Если с вызовом особых проблем нет: рекурсивная функция A() вызывает функцию B(), которая что-то делает и вызывает A(), то сразу возникает проблема с возвратом управления. Отработав рекурсивный вызов, функция A() должна получить управление, чтобы повторно вызвать B(), которая вновь её вызовет. Возврат управления, как следует по порядку в стеке обратно в B() - неправильное решение.
Программист не ограничен в выборе параметров и может комплектовать их именами функций. Иначе говоря, идеальное решение передать в A() имя B() и пусть сама A() делает вызов B(). В таком варианте не будет проблем с возвратом управления, да и реализация рекурсивного алгоритма будет прозрачнее.
Понимание и уровень рекурсии
Проблема разработки рекурсивных алгоритмов в том, что нужно иметь представление о динамике процесса. При использовании рекурсии в методах объектов, особенно на уровне абстрактного предка, появляется проблема понимания собственного алгоритма в контексте времени его исполнения.
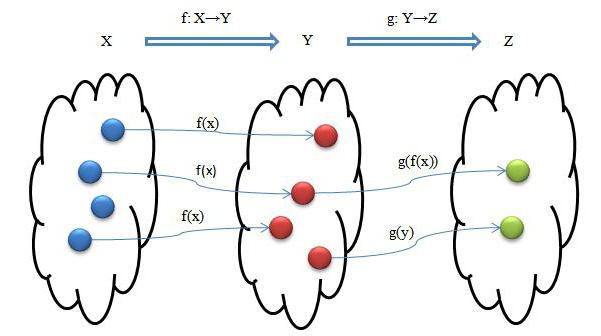
В настоящее время нет ограничений по уровню вложенности функций и вместимости стека в механизмах вызовов, но есть проблема понимания: в какой момент времени какой уровень данных или какое именно место в общем алгоритме выполнило вызов рекурсивной функции и на каком количестве вызовов самой себя она находится.
Существующие инструменты отладки часто бессильны подсказать программисту правильное решение.
Циклы и рекурсия
Считается, что циклическое выполнение эквивалентно рекурсии. Действительно, в некоторых случаях, рекурсивный алгоритм можно реализовать в синтаксисе условных и циклических конструкций.
Однако, если есть четкое понимание, что конкретная функция должна быть реализована посредством рекурсивного алгоритма, следует отказаться от любого внешнего варианта использования цикла или условных операторов.

Смысл здесь заключается в том, что рекурсивное решение в виде функции, использующей саму себя будет законченным, функционально полным алгоритмом. Этот алгоритм потребует от программиста усилий при его создании, понимания динамики работы алгоритма, но он будет окончательным решением, которое не потребует внешнего управления.
Любая комбинация внешних условных и циклических операторов не позволит представить рекурсивный алгоритм в виде полноценной законченной функции.
Консенсус рекурсии и ООП
Практически во всех вариантах разработки рекурсивного алгоритма возникает план разработать два алгоритма. Первый алгоритм формирует список будущих объектов (экземпляров), а второй алгоритм представляет собой собственно рекурсивную функцию.
Лучшим решением будет оформить рекурсию в виде одного свойства (метода), собственно содержащего рекурсивный алгоритм, а всю подготовительную работу вынести в конструктор объекта.
Рекурсивный алгоритм будет только тогда правильным решением, когда он работает только сам, без внешнего контроля и управления. Внешний алгоритм может только дать сигнал на работу. Результатом этой работы должно быть ожидаемое решение, без внешней поддержки.
Рекурсия должна быть всегда законченным самостоятельным решением.
Интуитивное понимание и функциональная полнота
Когда объектно-ориентированное программирование стало стандартом де-факто, стало очевидно: для эффективного кодирования следует изменить собственное мышление. Программист должен перейти от синтаксиса и семантики языка к динамике семантики в ходе исполнения алгоритма.
Характерная черта рекурсии: она может быть применена во всём:
- парсинг сайтов;
- поисковые операции;
- разбор текстовой информации;
- чтение или создание документов MS Word;
- выборка или анализ тегов...
Характерная черта ООП: оно дает возможность описать рекурсивный алгоритм на уровне абстрактного предка, но предусмотреть в нём обращение к уникальным потомкам, каждый из которых обладает собственной палитрой данных и свойств.

Рекурсия - идеальна, поскольку требует функциональной полноты своего алгоритма. ООП улучшает качественные показатели рекурсивного алгоритма, предоставляя ему доступ ко всем уникальным потомкам.


























