Математические задачи находят своё применение во многих науках. К таковым следует отнести не только физику, химию, технику и экономику, но также медицину, экологию и прочие дисциплины. Одним из важных понятий, которое следует освоить, чтобы находить решения важных дилемм, является производная функции. Физический смысл её объяснить совсем не так сложно, как может показаться непосвящённому в суть вопроса. Достаточно лишь найти подходящие примеры тому в реальной жизни и обычных бытовых ситуациях. На самом деле любой автомобилист справляется с подобной задачей каждый день, когда смотрит на спидометр, определяя скорость своей машины в конкретное мгновение фиксированного времени. Ведь именно в этом параметре заключена суть физического смысла производной.

Как найти скорость
Определить скорость движения человека по дороге, зная пройденное расстояние и время в пути, с лёгкостью может любой пятиклассник. Для этого следует первую из заданных величин разделить на вторую. Но не каждый из юных математиков знает о том, что в данный момент находит отношение приращений функции и аргумента. Действительно, если представить движение в виде графика, откладывая по оси ординат путь, а по абсциссе - время, это будет именно так.
Однако скорость пешехода или любого другого объекта, которую мы определяем на большом участке пути, считая движение равномерным, вполне может меняться. В физике известно множество форм движения. Оно может совершаться не только с постоянным ускорением, но замедляться и возрастать произвольным образом. Следует обратить внимание, что в данном случае линией, описывающей перемещение, будет уже не прямая. Графически она может принимать самые сложные конфигурации. Но для любой из точек графика мы всегда можем провести касательную, представленную линейной функцией.
Для уточнения параметра изменения перемещения в зависимости от времени приходится сокращать измеряемые отрезки. Когда же они станут бесконечно малыми, вычисляемая скорость окажется мгновенной. Данный опыт помогает нам дать определение производной. Физический смысл её также логически вытекает из подобных рассуждений.
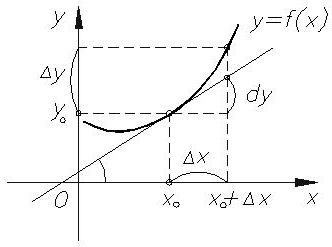
С точки зрения геометрии
Известно, что чем больше скорость тела, тем круче график зависимости перемещения от времени, а значит, и угол наклона касательной к графику в какой-то определённой точке. Показателем подобных изменений может стать тангенс угла между осью абсцисс и линией касательной. Как раз он определяет значение производной и вычисляется отношением длин противолежащего к прилежащему катету в прямоугольном треугольнике, образованном перпендикуляром, опущенным из некоторой точки на ось абсцисс.
В этом заключается геометрический смысл первой производной. Физический же раскрывается в том, что величина противолежащего катета в нашем случае представляет собой пройденный путь, а прилежащего – время. При этом отношением их является скорость. И снова мы приходим к выводу, что мгновенная скорость, определяемая при стремлении обоих промежутков к бесконечно малому, и является сутью понятия производной, указывая на её физический смысл. Второй производной в данном примере будет ускорение тела, демонстрирующее, в свою очередь, степень изменения скорости.

Примеры нахождения производных в физике
Производная – это показатель скорости изменения любой функции, даже когда речь не идёт о движении в прямом смысле слова. Чтобы наглядно продемонстрировать это, приведём несколько конкретных примеров. Допустим, сила тока, завися от времени, изменяется согласно следующему закону: I = 0,4t2. Требуется найти значение скорости, с которой происходит изменение этого параметра в конце 8-й секунды процесса. Заметим, что сама искомая величина, как можно судить из уравнения, постоянно возрастает.
Для решения требуется найти первую производную, физический смысл которой был рассмотрен ранее. Здесь dI/dt = 0,8t. Далее найдём оную при t=8, получим, что скорость, с которой происходит изменение силы тока, равна 6,4 A/c. Здесь считается, что сила тока измеряется в амперах, а время, соответственно, в секундах.
Всё изменчиво
Видимый окружающий мир, состоящий из материи, постоянно претерпевает изменения, находясь в движении протекающих в нём разнообразных процессов. Для описания их можно использовать самые разные параметры. Если они объединены зависимостью, то математически записываются в виде функции, наглядно показывающей их изменения. А где есть движение (в каком бы виде оно ни выражалось), там существует и производная, физический смысл которой мы и рассматриваем в настоящий момент.

По этому поводу следующий пример. Допустим, температура тела изменяется по закону T=0,2t2. Следует найти скорость его нагревания в конце 10-й секунды. Решение задачи производится способом, аналогичным описанному в предыдущем случае. То есть мы находим производную и подставляем в неё значение для t = 10, получаем T = 0,4t = 4. Значит, окончательным ответом считается 4 градуса за секунду, то есть процесс нагревания и изменение температуры, измеряемой в градусах, происходит именно с такой скоростью.
Решение практических задач
Конечно, в реальной жизни всё бывает гораздо сложнее, чем в теоретических задачах. На практике значение величин определяется обычно в ходе эксперимента. При этом используются приборы, которые выдают показания при измерениях с определённой погрешностью. Поэтому при вычислениях приходится иметь дело с приближёнными значениями параметров и прибегать к округлениям неудобных чисел, а также другим упрощениям. Приняв это ко вниманию, снова приступим к задачам на физический смысл производной, учитывая, что они являются лишь некоей математической моделью происходящих в природе сложнейших процессов.
Извержение вулкана
Представим, что происходит извержение вулкана. Насколько он может быть опасен? Для выяснения этого вопроса необходимо рассмотреть множество факторов. Мы постараемся учесть один из них.

Из жерла "огненного чудовища" выбрасываются вертикально вверх камни, имеющие начальную скорость с момента выхода наружу 120 м/с. Необходимо просчитать, какой они могут достигнуть максимальной высоты.
Для нахождения искомого значения составим уравнение зависимости высоты H, измеряемой в метрах, от прочих величин. К таковым относятся начальная скорость и время. Значение ускорения считаем известным и приблизительно равным 10 м/с2.

Частная производная
Рассмотрим теперь физический смысл производной функции немного с другой стороны, ведь само уравнение может содержать не одну, а несколько переменных. К примеру, в предыдущей задаче зависимость высоты подъёма камней, выбрасываемых из жерла вулкана, определялась не только изменением временных характеристик, но и значением начальной скорости. Последняя считалась постоянной, фиксированной величиной. Но в других задачах с совершенно иными условиями всё могло быть иначе. Если величин, от которых зависит сложная функция, несколько, расчёты производятся согласно указанным ниже формулам.
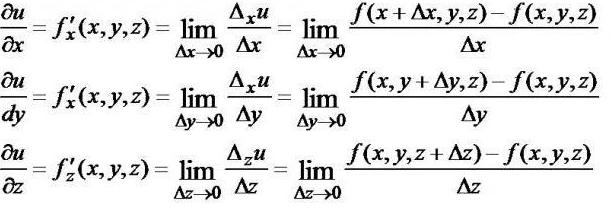
Физический смысл частой производной следует определять, как и в обычном случае. Это скорость изменения функции в некоторой определённой точке при росте параметра переменной. Она вычисляется таким образом, что все остальные составляющие принимаются за постоянные, лишь только один рассматривается как переменная. Далее всё происходит по обычным правилам.
Незаменимый советник по многим вопросам
Понимая физический смысл производной, примеры решения запутанных и сложных проблем, ответ в которых позволяют найти подобные знания, привести несложно. Если у нас есть функция, описывающая расход горючего в зависимости от скорости автомобиля, можем рассчитать, при каких параметрах последней расход бензина будет наименьшим.
В медицине можно предвидеть, каким образом будет реагировать человеческий организм на прописанное врачом лекарство. Приём препарата сказывается на самых разных физиологических показателях. К ним относятся изменения артериального давления, пульса, температуры тела и многого другого. Все они зависят от дозы принимаемого лекарственного средства. Данные расчёты помогают предвидеть ход лечения, как в благоприятных проявлениях, так и в нежелательных случайностях, способных фатальным образом отразиться на изменениях в организме больного.

Несомненно, важным оказывается понимание физического смысла производной в технических вопросах, в частности в электротехнике, электронике, конструировании и строительстве.
Тормозной путь
Рассмотрим очередную задачу. Двигаясь с постоянной скоростью, автомобиль, приближаясь к мосту, за 10 секунд до въезда вынужден был затормозить, так как водитель заметил дорожный знак, запрещающий движение со скоростью более 36 км/час. Не нарушил ли правила шофёр, если тормозной путь его можно описать формулой S = 26t – t2?
Вычислив первую производную, найдём формулу для скорости, получим v = 28 – 2t. Далее подставим в указанное выражение значение t=10.
Так как эта величина была выражена в секундах, скорость оказывается равной 8 м/с, а значит, 28,8 км/час. Это даёт возможность понять, что шофёр начал тормозить вовремя и не нарушил правила движения, а значит, и предел указанной на знаке скорости.
Подобное доказывает важность физического смысла производной. Пример решения данной задачи демонстрирует широту использования этого понятия в самых разных сферах жизни. В том числе и в бытовых ситуациях.

Производная в экономике
До XIX столетия экономисты в основном оперировали средними величинами, будь то производительность труда или цена на выпускаемую продукцию. Но с некоторого момента для составления эффективных прогнозов в данной области больше стали необходимы предельные величины. К таковым можно отнести предельную полезность, доход или издержки. Понимание этого дало толчок к созданию совершенно нового инструмента в экономических исследованиях, который существует и развивается вот уже более ста лет.
Для составления подобных расчётов, где главенствуют такие понятия, как минимум и максимум, просто необходимо понимание геометрического и физического смысла производной. Среди создателей теоретической основы указанных дисциплин можно назвать таких видных английских и австрийских экономистов, как У. С. Джевонс, К. Менгер и других. Конечно, предельные величины в экономических выкладках не всегда использовать удобно. А, к примеру, квартальные отчёты не обязательно укладываются в существующую схему, но всё же применение подобной теории во многих случаях бывает полезно и эффективно.



























