Что такое переменные? Переменная величина в математике

Значение переменных в математике велико, ведь за время ее существования ученые успели совершить множество открытий в данной области, и, чтобы кратко и ясно изложить ту или иную теорему, мы пользуемся переменными для записи соответствующих формул. Например, теорема Пифагора о прямоугольном треугольнике: a² = b² + c². Чем каждый раз при решении задачи писать: по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов - мы записываем это формулой, и все сразу становится понятно.

Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.

Понятие переменной

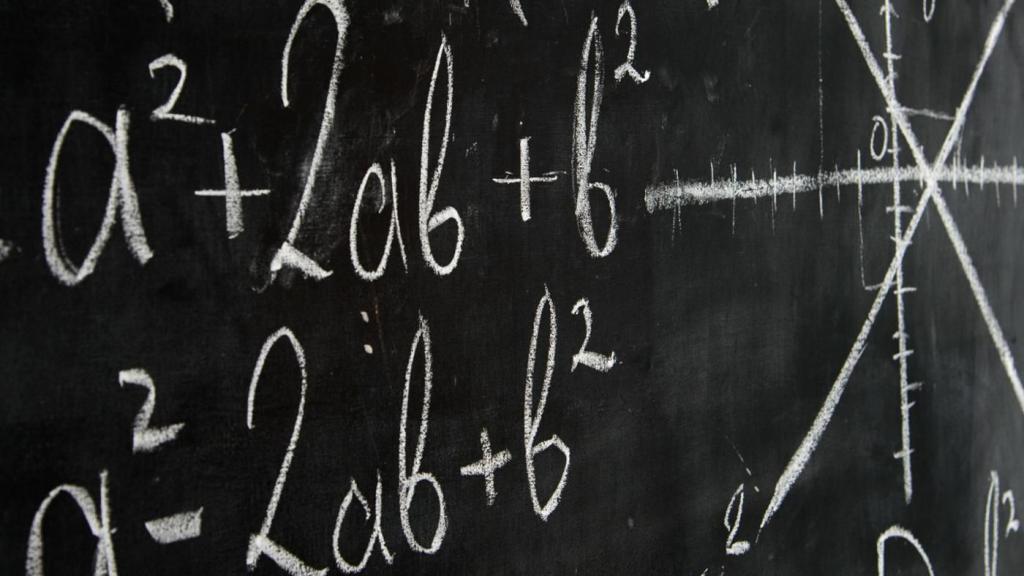
Для начала узнаем, что такое переменная? Это численная величина, которая может принимать множество значений. Она не может быть постоянной, так как в разных задачах и уравнениях для удобства решения мы принимаем за переменную разные числа, то есть, например, z - это общее обозначение для каждой из величин, за которые ее принимают. Обычно их обозначают буквами латинского или греческого алфавита (x, y, a, b и так далее).

Есть разные виды переменных. Ими задаются как некоторые физические величины - путь (S), время (t), так и просто неизвестные значения в уравнениях, функциях и других выражениях.

Например, есть формула: S = Vt. Здесь переменными обозначаются определенные величины, имеющие отношение к реальному миру - путь, скорость и время.

А есть уравнение вида: 3x - 16 = 12x. Здесь уже за x принимается абстрактное число, которое имеет смысл в данной записи.

Виды величин

Под величиной имеется в виду то, что выражает свойства определенного предмета, вещества или явления. К примеру, температура воздуха, масса животного, процентное содержание витаминов в таблетке - это все величины, числовые значения которых можно вычислить.

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

Возьмем прямолинейное равномерное движение. Точка в пространстве движется с одинаковой скоростью на каждом промежутке времени. То есть изменяются время и расстояние, а скорость остается одинаковой. В данном примере время и расстояние - переменные величины, а скорость - постоянная.

Или, например, “пи”. Это иррациональное число, которое продолжается без повторяющейся последовательности цифр и не может быть записано полностью, поэтому в математике оно выражается общепринятым символом, который принимает только значение данной бесконечной дроби. То есть “пи” - это постоянная величина.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

x⁴ + 15x² + 7 = 0

За x² принимаем некое k, и уравнение приобретает понятный вид:

x² = k, при k ≥ 0

k² + 15k + 7 = 0

Вот какую пользу в математику несет введение переменных.

Неравенства, примеры решения

Неравенство представляет собой запись, в которой два математических выражения или два числа связаны знаками сравнения: <, >, ≤, ≥. Они бывают строгими и обозначаются знаками < и > или нестрогими со знаками ≤, ≥.

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

1. При переносе числа из одной части неравенства в другую меняем его знак на противоположный.
2. При умножении или делении частей неравенства на отрицательное число их знаки меняются на противоположные.
3. Если умножить или разделить обе части неравенства на положительное число, то получится неравенство, равное исходному.

Решить неравенство - значит найти все допустимые значения переменной.

Пример с одной переменной:

10x - 50 > 150

Решаем, как обычное линейное уравнение - переносим слагаемые с переменной влево, без переменной - вправо и приводим подобные члены:

10x > 200

Делим обе части неравенства на 10 и получаем:

x > 20

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

6x - 12 ≥ 18

6x ≥ 30

x ≥ 5

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

x ∈ [5; +∞)

Квадратные неравенства

Если взять квадратное уравнение вида ax² + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

y = ax² + bx + c - это квадратичная функция. Ее мы можем решить с помощью дискриминанта, либо используя теорему Виета. Вспомним, как решаются подобные уравнения:

1) y = x² + 12x + 11 - функция является параболой. Ее ветви направлены вверх, так как знак коэффициента "a" положительный.

2) x² + 12x + 11 = 0 - приравниваем к нулю и решаем с помощью дискриминанта.

a = 1, b = 12, c = 11

D = b² - 4ac= 144 - 44 = 100 > 0, 2 корня

По формуле корней квадратного уравнения получаем:

x₁ = -1, x₂ = -11

Или можно было решить это уравнение по теореме Виета:

x₁ + x₂ = -b/a, x₁ + x₂ = -12

x₁x₂ = c/a, x₁x₂ = 11

Методом подбора получаем такие же корни уравнения.

Парабола

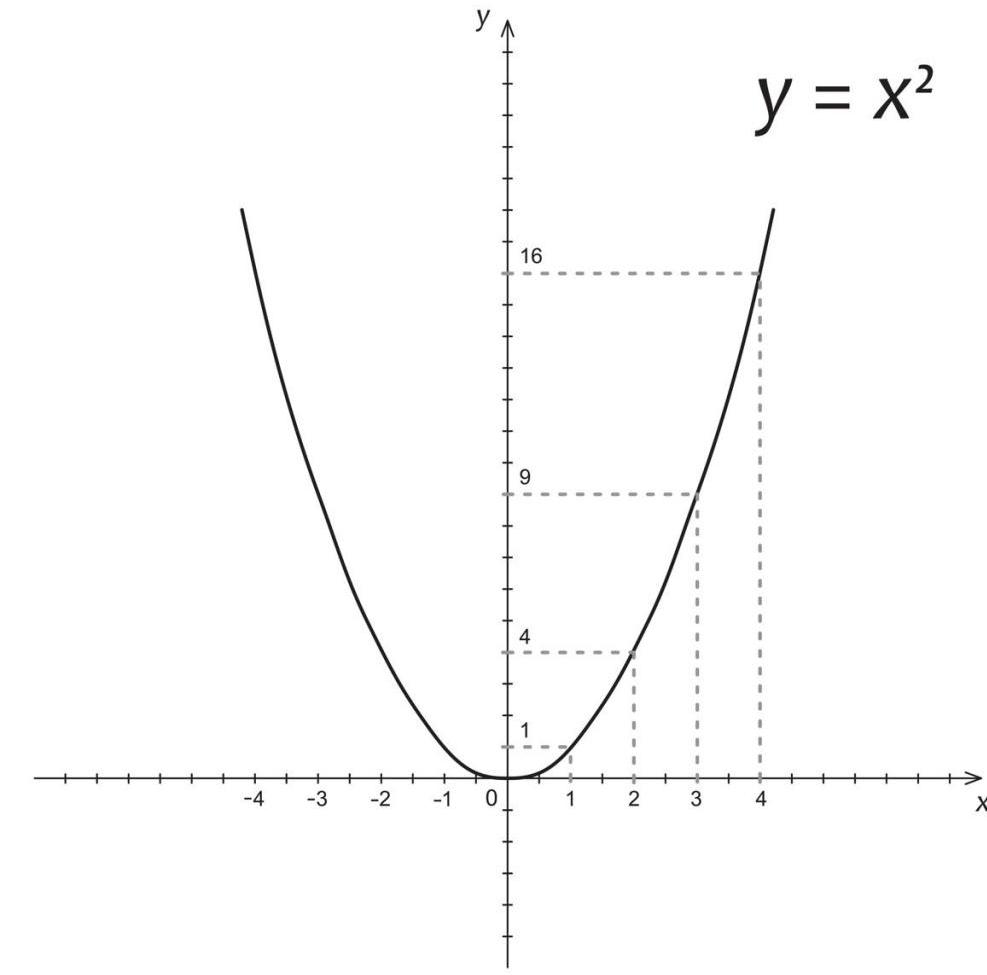
Итак, первый способ решения квадратного неравенства - это парабола. Алгоритм ее решения таков:

1. Определяем, куда направлены ветви параболы.

2. Приравниваем функцию к нулю и находим корни уравнения.

3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.

Решим неравенство x² + x - 12 > 0

Выписываем в виде функции:

1) y = x² + x - 12 - парабола, ветви вверх.

Приравниваем к нулю.

2) x² + x -12 = 0

Дальше решаем как квадратное уравнение и находим нули функции:

x₁ = 3, x₂ = -4

3) Изображаем числовую прямую и на ней точки 3 и -4. Парабола пройдет через них, ветвями вверх и ответом к неравенству будет множество положительных значений, то есть (-∞; -4), (3; +∞).

Метод интервалов

Второй способ - это метод интервалов. Алгоритм его решения:

1. Находим корни уравнения, при которых неравенство равно нулю.

2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

Решим неравенство (x - 4)(x - 5)(x + 7) ≤ 0

1) Нули неравенства: 4, 5 и -7.

2) Изображаем их на числовой прямой.

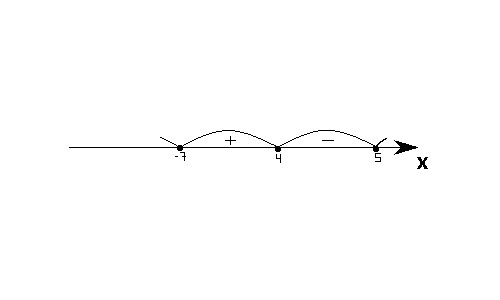
3) Определяем знаки интервалов.

Ответ: (-∞; -7]; [4; 5].

Решим еще одно неравенство: x²(3x - 6)(x + 2)(x - 1) > 0

1. Нули неравенства: 0, 2, -2 и 1.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Прямая делится на промежутки - от -2 до 0, от 0 до 1, от 1 до 2.

Возьмем значение на первом промежутке - (-1). Подставляем в неравенство. При данном значении неравенство становится положительным, значит и знак на этом промежутке будет +.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Ответ: (-2; 0), (1; 2).

Системы уравнений

Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.

Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.

Мы изучим решение систем уравнений с двумя переменными. Есть два способа их решения - метод подстановки или алгебраический метод.

Алгебраический метод

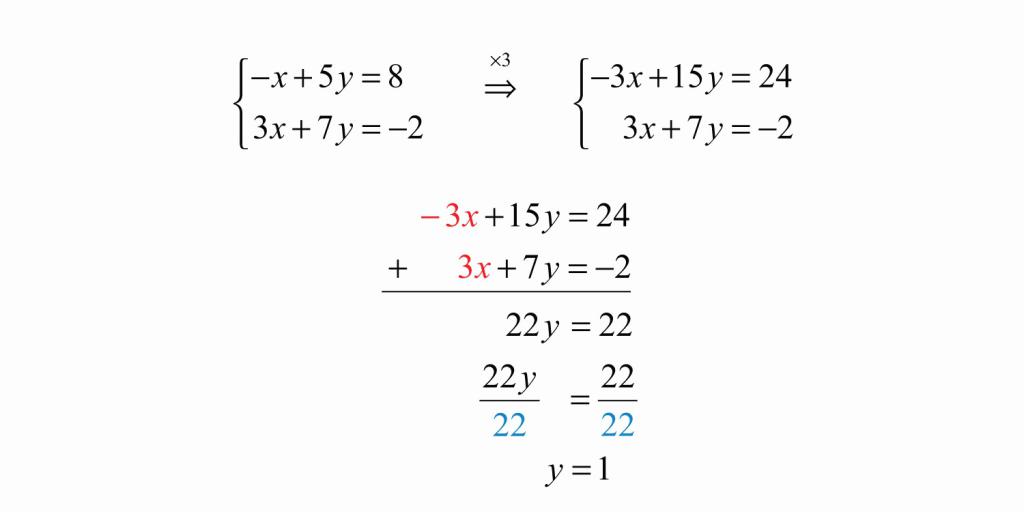
Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

-x + 5y = 8 , при y = 1

-x + 5 = 8

Решаем получившееся уравнение и находим икс.

-x = -5 + 8

-x = 3

x = -3

Главное в решении системы - правильно записать ответ. Многие школьники делают ошибку и пишут:

Ответ: -3, 1.

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

(-3; 1)

Метод подстановки

Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.

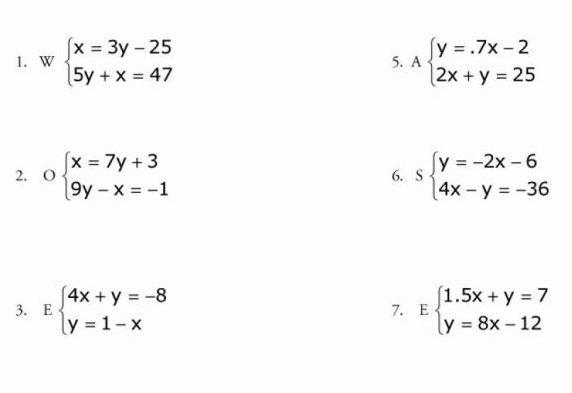
В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:

5y + 3y - 25 = 47

Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:

8y = 72

y = 9

Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:

x = 3y - 25, при y = 9

x = 27 - 25

x = 2

Ответ: (2; 9).