Формула площади правильной пирамиды. Решение геометрической задачи

В данной статье рассмотрим, как рассчитывать площадь правильной пирамиды. Геометрические свойства фигур в пространстве изучает стереометрия. Этот раздел геометрии использует понятия длин отрезков и углов между ними для определения таких характеристик фигур, как площадь или объем.

Что это за фигура?

Прежде чем переходить к рассмотрению конкретных формул площади правильной пирамиды (боковая поверхности и основания), следует пояснить, что она представляет собой с точки зрения геометрии. Поясним.

Пирамидой называют любой геометрический объект в пространстве, который образован в результате соединения одной точки со всеми вершинами некоторого многоугольника. Так образуется фигура. Общая точка называется вершиной и плоскости многоугольника не принадлежит.

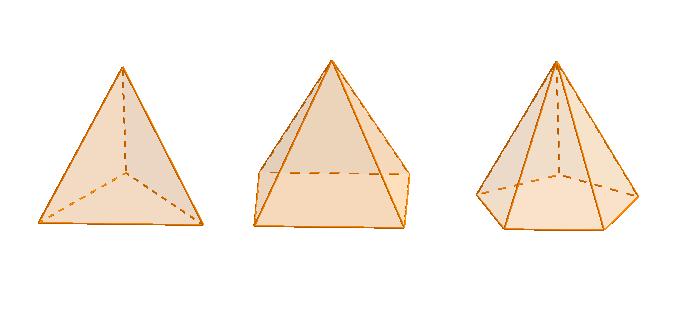
Выше показаны три разных пирамиды. Видно, что отличаются они количеством сторон многоугольного основания (три, четыре и пять). Однако все эти фигуры объединяет то, что их боковая поверхность состоит из треугольников. Количество их разное, оно равно числу сторон основания.

Из рисунка видно, что любая пирамида состоит из ребер, вершин и граней. Их совокупность образует единый объект. Если из его вершины (точка пересечения боковых треугольников) опустить перпендикуляр к основанию, то его длина будет высотой фигуры. Если этот отрезок заканчивается в центре основания, то такая пирамида будет называться прямой. С этим разобрались, идем далее.

Прямая пирамида, основание которой является равносторонним и равноугольным многоугольником, называется правильной. Приведем пример. Пирамида Хеопса - это правильная четырехугольная фигура, поскольку она является прямой и имеет квадратное основание.

Формулы для определения значений

В стереометрии для изучения площади правильной пирамиды и других объемных фигур используют их развертки. Поясним графически. На рисунке показано, что представляет собой развертка правильной четырехугольной пирамиды. Теперь становится более понятно, как производить расчеты.

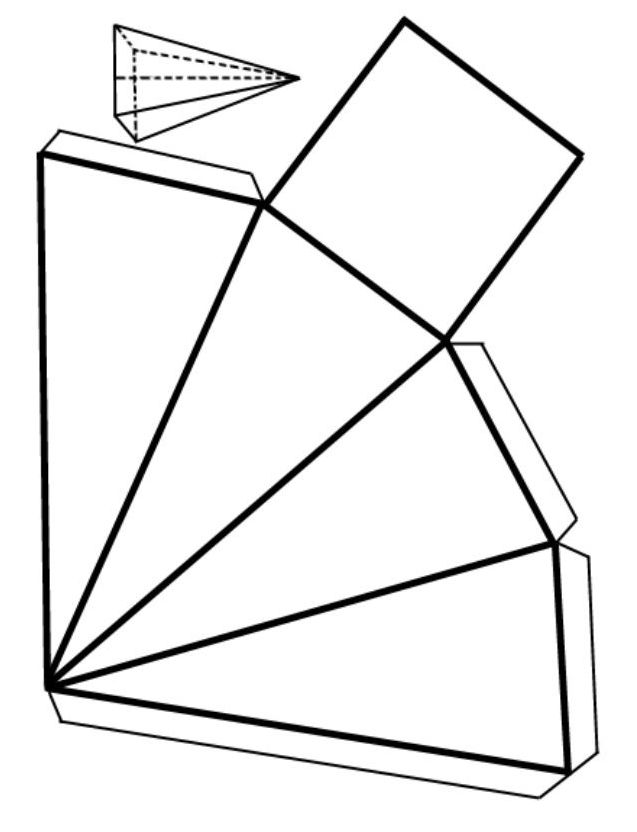
Видно, что площадь правильной пирамиды имеет две составляющие: основание и боковую поверхность. Присвоим переменные.

Обозначим площадь основания символом S_o. Для вычисления этой величины существует универсальная формула для правильного n-угольника. Она имеет вид:

S_n = n / 4 * a² * ctg (pi/n).

Здесь n - количество сторон основания, a - сторона n-угольника.

В правильной пирамиде все треугольники, которые образуют боковую поверхность, равны между собой и в общем случае являются равнобедренными. Это означает, что для определения у фигуры площади боковой поверхности (обозначим ее S_b) необходимо найти этот параметр у одного треугольника, а затем, умножить на их количество. Запишем формулу. Площадь боковой стороны правильной пирамиды рассчитывается так:

S_b1 = 1 / 2 * a * h_b.

Здесь h_b - это высота треугольника, которая называется апофемой пирамиды .

Поскольку количество треугольников равно числу сторон n-угольного основания, то получаем формулу для вычисления величины S_b:

S_b = n * S_b1 = n * a * h_b / 2.

Тогда общую площадь правильной пирамиды можно вычислить по формуле:

S = S_o + S_b = n / 4 * a² * ctg(pi/n) + n * a * h_b / 2.

Решение задачи

Условие. Известно, что правильная четырехугольная пирамида имеет длину стороны основания 10 см и высоту 12 см. Чему равна площадь ее поверхности?

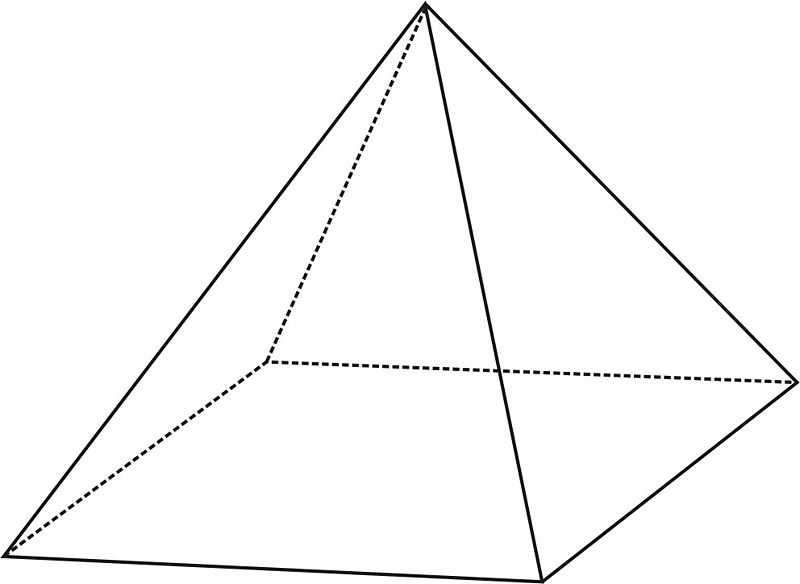
Решение. Площадь поверхности основания (квадрата) равна:

S_o = a² = 100 см².

Чтобы вычислить площадь боковой поверхности , необходимо знать апофему h_b фигуры. Если рассмотреть прямоугольный треугольник внутри пирамиды, то апофема, являющаяся в нем гипотенузой, вычисляется так:

h_b = √(a² / 4 + h²) = 13 см.

Тогда площадь боковой поверхности правильной пирамиды равна:

S_b = n * a * h_b / 2 = 4 * 10 * 13 / 2 = 260 см².

Складывая полученные значения S_o и S_b, приходим к ответу на вопрос задачи: S = 360 см².

В статье рассмотрено, как найти площадь фигуры, называемой правильной пирамидой.