Изучая объемные фигуры в курсе стереометрии, школьники часто сталкиваются с задачей определения площади их поверхности. Успешное решение этой задачи возможно, если четко представлять, с какой фигурой ведется работа. Данная статья посвящена вопросу определения площади поверхности правильной пирамиды (четырехугольной).
Описание фигуры
Начнем раскрытие вопроса статьи с определения правильной четырехугольной пирамиды. Под ней в геометрии понимают фигуру в пространстве, которая образована одним квадратом и четырьмя одинаковыми равнобедренными треугольниками (при определенных параметрах фигуры эти треугольники могут быть равносторонними). Пример рассматриваемой фигуры показан ниже.

Каждый равнобедренный треугольник пересекается по боковым граням с двумя соседними треугольниками, и по грани основания - с квадратом. Кроме того, все четыре треугольника пересекаются в одной точке, которая носит название главной вершины пирамиды. Помимо нее, фигура имеет еще четыре вершины, но все они принадлежат основанию.
Четырехугольной эта пирамида называется потому, что ее основание является четырехугольником. А правильной она считается потому, что это основание представляет собой квадрат, и сама фигура является прямой. Последнее означает, что опущенный с вершины перпендикуляр на квадрат пересекает его точно в геометрическом центре.
Что собой представляет площадь поверхности правильной пирамиды (четырехугольной)
Многим будет нелегко ответить на этот вопрос. Действительно, мы рассматриваем объемную фигуру, а когда говорят о площадях, то имеют в виду силуэт на плоскости. В связи со сказанным в геометрии для вычисления площадей пространственных объектов используют их плоские развертки.

Развертку рассматриваемой пирамиды получить несложно. Предположим, что у нас имеется бумажная фигура с квадратным основанием. Возьмем ножницы и отрежем от нее квадрат. Затем разрежем вдоль бокового ребра (отрезок пересечения треугольников) пирамидальную поверхность и развернем ее в плоскую интерпретацию. В результате этих действий у нас получится плоская фигура, подобная той, что показана на рисунке.
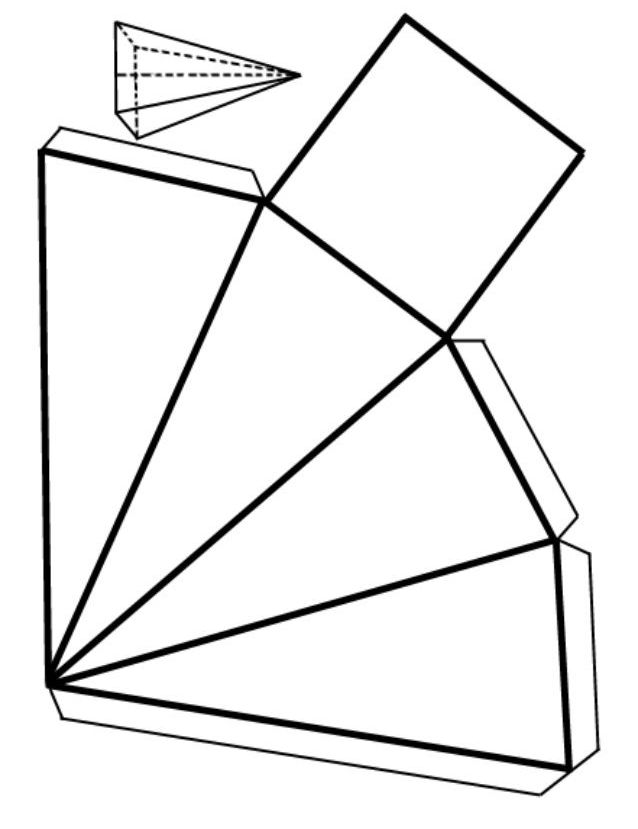
Таким образом, отвечая на вопрос, как найти площадь правильной четырехугольной пирамиды, следует сказать, что для этого нужно сложить площадь квадрата и площади четырех одинаковых треугольников.
Формулы для нахождения величины
Из планиметрии известно, что расчет площади производится с учетом знания линейных параметров плоской фигуры. В нашем случае речь идет о двух типах объектов: равнобедренном треугольнике и квадрате.
Обозначим сторону четырехугольника буквой a, а высоту треугольника hb (она называется апофемой пирамиды). Тогда для площади So квадрата можно записать:
So = a2
Площадь же треугольника S3 будет равна:
S3 = 1 / 2 * a * hb
Поскольку треугольников с площадью S3 в рассматриваемой пирамиде четыре штуки, то формула площади поверхности правильной пирамиды (четырехугольной) примет вид:
S = So + 4 * S3 = a2 + 4 / 2 * a * hb = a * (a + 2 * hb)
При решении некоторых задач вместо апофемы hb может быть известен другой линейный параметр пирамиды - высота h. Поэтому будет полезным, если мы здесь приведем формулу для S через параметры a и h.
Решить поставленную задачу можно, если увидеть внутри пирамиды треугольник прямоугольный, и рассчитать гипотенузу-апофему по следующей формуле:
hb = √(h2 + a2 / 4)
Подставляя это выражение в записанную выше формулу для S, получаем:
S = a * (a + 2 * √(h2 + a2 / 4))
Это выражение выглядит несколько сложнее, чем первое. Тем не менее, оно чаще используется при рассмотрении геометрических проблем с четырехугольной пирамидой.
Записанные формулы для площади рассматриваемой фигуры можно не запоминать, важно лишь ясно представлять развертку пирамиды и уметь находить площадь треугольника.
Использование формулы площади четырехугольной пирамиды на примере сооружения Хеопса

Конечно же, речь идет о пирамиде Хеопса - самой знаменитой каменной постройки за всю известную нам историю. Рассчитаем площадь поверхности этого гиганта, используя следующие данные о нем:
- среднее значение длины стороны основания равно 230,363 метра;
- начальная высота сооружения составляла 146,50 метра.
Чтобы найти искомую площадь, следует воспользоваться второй формулой, приведенной в предыдущем пункте статьи. Сделаем это:
S = a * (a +2 * √(h2 + a2 / 4)) = 230,3632 + 230,363 * 2 * √(146,502 + 230,3632 / 4) ≈ 138 927 м2
Чтобы понять, насколько огромно рассчитанное значение, сравним его с параметрами футбольного поля (5 000 м2). Полная площадь поверхности правильной четырехугольной пирамиды Хеопса почти в 28 раз больше величины площадки для игры.



























