Формулы площади четырехугольной пирамиды произвольного типа и правильной. Пример геометрической задачи

Четырехугольная пирамида, пожалуй, самая известная фигура из данного класса объемных геометрических объектов. Ее свойства и характеристики изучают в старших классах школ. Данная статья призвана ответить на вопрос о том, по какой формуле площадь четырехугольной пирамиды рассчитывается.

Четырехугольная пирамида

Чтобы не ходить далеко за примерами этой фигуры, сразу скажем, что великая пирамида Хеопса является самой известной четырехугольной правильной фигурой.

С чисто геометрической точки зрения пирамида четырехугольная представляет собой объект, образованный пятью гранями: четырьмя треугольниками и одним плоским четырехугольником. Построить в пространстве эту фигуру не представляет никакого труда. Для этого берется плоский четырехугольник (квадрат, прямоугольник, ромб, параллелограмм и так далее), а затем все его вершины соединяются с одной единственной точкой в пространстве, которая станет вершиной пирамиды. В результате таких простых геометрических операций мы получаем четырехугольную пирамиду.

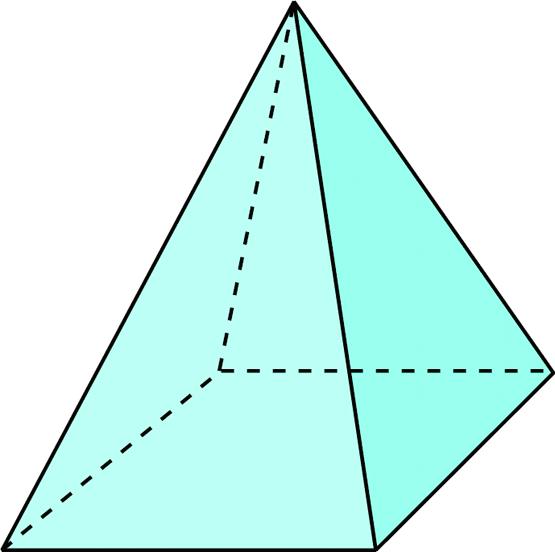
Видно, что фигура состоит из пяти граней, пяти вершин, одна из которых является главной, и восьми ребер (4 относятся к основанию, 4 принадлежат треугольникам).

Не все четырехугольные пирамиды имеют одинаковую форму. Существует несколько типов этих фигур. Например, пирамиды бывают наклонные и прямые. В первом случае перпендикуляр, который опущен из вершины к четырехугольному основанию, пересекает последнее в точке, не совпадающей с его центром. В случае же прямой фигуры точка пересечения перпендикуляра плоскости основания и является его центром. Напомним, что центр выпуклого четырехугольника лежит в точке пересечения двух диагоналей.

Помимо наклонных и прямых фигур, четырехугольные пирамиды могут быть правильными и неправильными. Любая пирамида с квадратным основанием, которая является прямой, будет правильной. Правильные пирамиды отличаются друг от друга размерами (длиной стороны квадрата a, длиной ребер боковых b и высотой h). При выполнении вычислений различных геометрических характеристик с правильными пирамидами, в виду их высокой симметрии, удобно работать. Кроме того, многие свойства этих фигур описываются специальными выражениями, включая формулу площади правильной пирамиды четырехугольной.

Площадь пирамиды с четырехугольным основанием произвольного типа

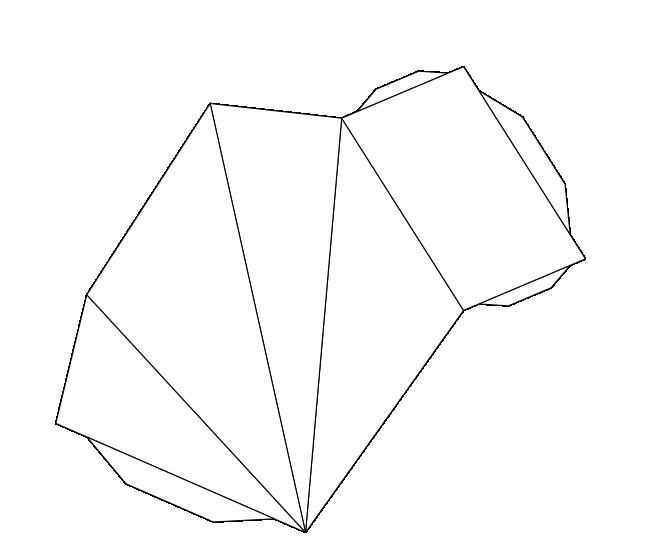
Чтобы определить площадь любого многогранника, необходимо сложить площади всех его сторон. Изучаемая фигура имеет пять сторон, четыре из которых являются треугольными. Их площади найти несложно, если знать высоту каждого треугольника h_bi (она является апофемой пирамиды) и длину каждой стороны четырехугольника a_i. Тогда для четырехугольной пирамиды формула площади боковой поверхности примет вид:

S_b = 1/2*∑_i=1⁴(a_i*h_bi)

К значению S_b следует добавить площадь четырехугольника S₄, чтобы получить площадь полной поверхности пирамиды. Величину S₄ несложно определить, если известны стороны a_i и углы четырехугольника.

Площадь правильной фигуры

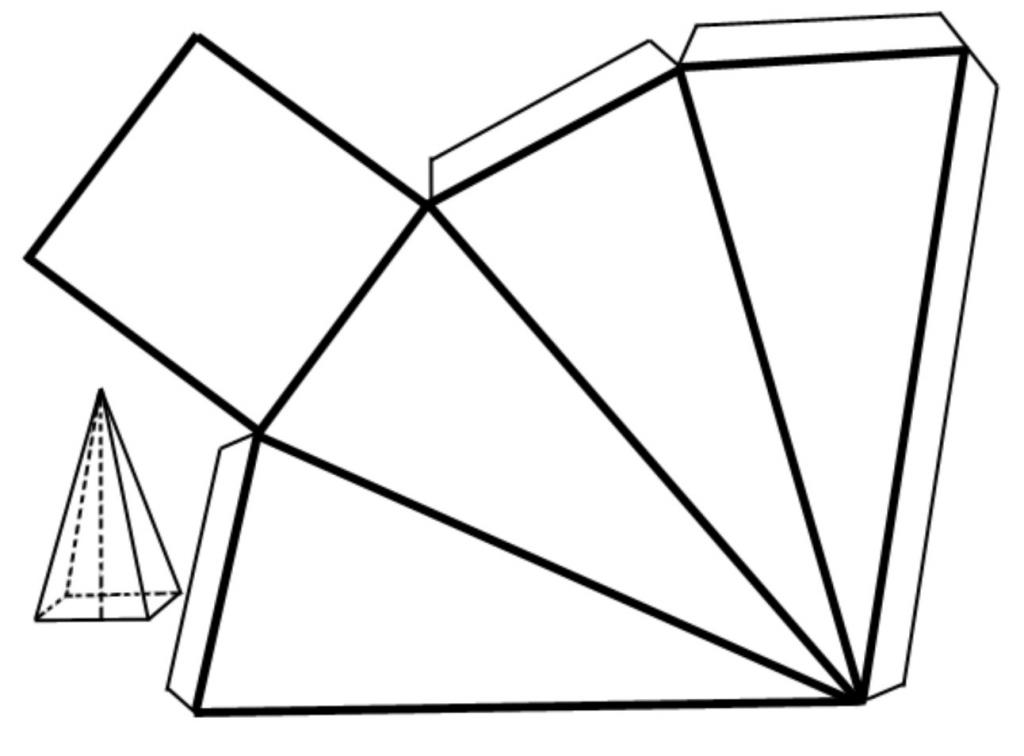
Как было сказано выше, для правильной пирамиды четырехугольной формула площади поверхности имеет конкретный вид. Получим ее.

Начнем с рассмотрения площади основания. Поскольку оно представляет собой обычный квадрат, то его площадь вычисляется с помощью простого выражения:

S₄ = a²

Теперь обратим внимание на боковую поверхность. Представлена она четырьмя одинаковыми треугольниками, которые к тому же являются равнобедренными, или равносторонними. Все апофемы треугольников равны, обозначим их длину h_b. Площадь поверхности боковой будет равна:

S_b = 2*h_b*a

Тогда формула площади поверхности четырехугольной пирамиды правильной примет следующий вид:

S = S₄ + S_b = a² + 2*h_b*a

Решение задачи по геометрии

Известно, что ребро правильной пирамиды, которая имеет квадрат в основании, равно длине диагонали этого основания. Зная, что сторона квадрата равна 8 см, необходимо определить площадь всех граней данной фигуры.

Поскольку диагональ квадрата d равна длине ребра бокового b, то получаем:

b = d = a*√2

Теперь следует увидеть, что в изучаемой пирамиде ребро b, апофема h_b и половина стороны квадрата образуют треугольник с углом 90^o. Этот факт позволяет воспользоваться теоремой Пифагора для определения h_b:

h_b = √(b² - a²/4) = √(2*a² - a²/4) = a*√7/2

Теперь можно применить формулу площади четырехугольной пирамиды:

S = a² + 2*h_b*a = a² + 2*a*√7/2*a = a²*(1+√7)

Остается подставить значение стороны квадрата из условия и записать ответ: S = 233,33 см².