Геометрические фигуры в пространстве являются объектом изучения стереометрии, курс которой проходят школьники в старших классах. Данная статья посвящена такому совершенному многограннику, как призма. Рассмотрим подробнее свойства призмы и приведем формулы, которые служат для их количественного описания.
Что это - призма?
Каждый представляет, как выглядит параллелепипед или куб. Обе фигуры являются призмами. Однако, класс призм гораздо более разнообразен. В геометрии этой фигуре дается следующее определение: призмой является всякий многогранник в пространстве, который образован двумя параллельными и одинаковыми многоугольными сторонами и несколькими параллелограммами. Одинаковые параллельные грани фигуры называются ее основаниями (верхним и нижним). Параллелограммы же - это боковые грани фигуры, соединяющие стороны основания друг с другом.
Если основание представлено n-угольником, где n - целое число, тогда фигура будет состоять из 2+n граней, 2*n вершин и 3*n ребер. Грани и ребра относятся к одному из двух типов: либо они принадлежат боковой поверхности, либо основаниям. Что касается вершин, то все они являются равноправными и относятся к основаниям призмы.
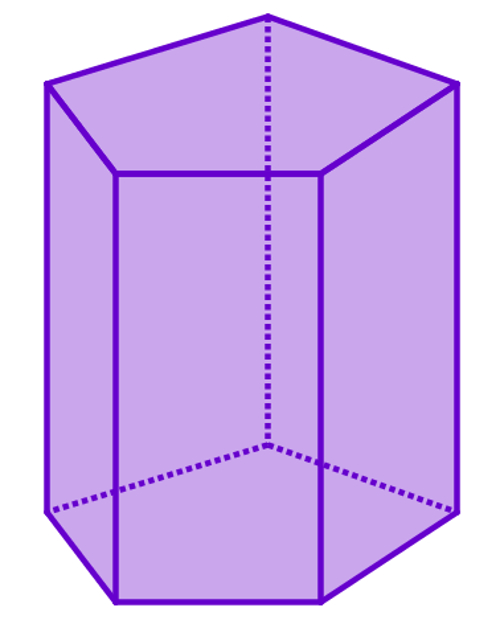
Виды фигур изучаемого класса
Изучая свойства призмы, следует перечислить возможные виды этой фигуры:
- Выпуклые и вогнутые. Разница между ними заключается в форме многоугольного основания. Если оно является вогнутым, то таковой также будет объемная фигура, и наоборот.
- Прямые и наклонные. У прямой призмы боковые грани представлены либо прямоугольниками, либо квадратами. У наклонной фигуры боковые грани являются параллелограммами общего типа или ромбами.
- Неправильные и правильные. Чтобы изучаемая фигура была правильной, она должна быть прямой и иметь правильное основание. Примером последнего являются такие плоские фигуры, как равносторонний треугольник или квадрат.
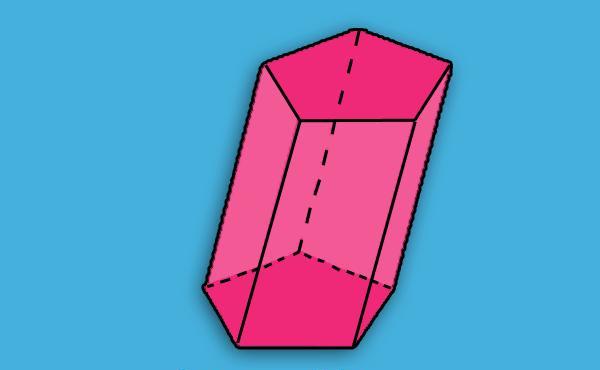
Название призмы образуется с учетом перечисленной классификации. Например, упомянутый выше параллелепипед с прямыми углами или куб, называются правильной четырехугольной призмой. Правильные призмы, ввиду их высокой симметрии, удобно изучать. Их свойства выражаются в виде конкретных математических формул.
Площадь призмы
Когда рассматривают такое свойство призмы, как ее площадь, то имеют в виду суммарную площадь всех ее граней. Представить эту величину проще всего, если сделать развертку фигуры, то есть разложить все грани на одну плоскость. Ниже на рисунке показаны для примера развертки двух призм.
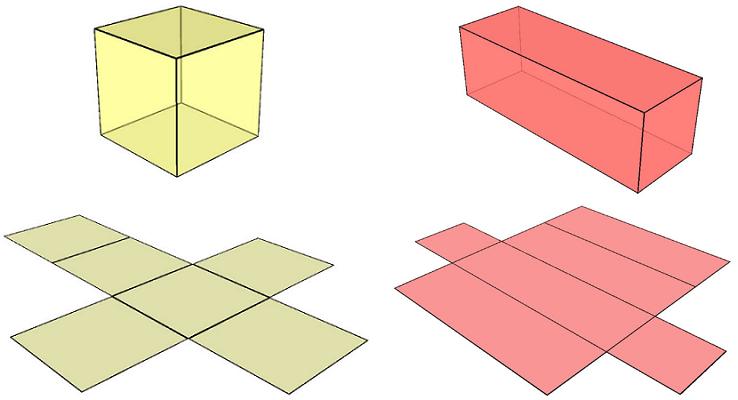
Для произвольной призмы формула площади ее развертки в общем виде может быть записана так:
S = 2*So + b*Psr.
Поясним обозначения. Величина So - это площадь одного основания, b - длина бокового ребра, Psr - периметр среза, который перпендикулярен боковым параллелограммам фигуры.
Записанной формулой часто пользуются для определения площадей наклонных призм. В случае правильной призмы выражение для S приобретет конкретный вид:
S = n/2*a2*ctg(pi/n) + n*b*a .
Первое слагаемое в выражении представляет площадь двух оснований правильной призмы, второе слагаемое - это площадь боковых прямоугольников. Здесь a - длина стороны правильного n-угольника. Отметим, что длина бокового ребра b для правильной призмы является также ее высотой h, поэтому в формуле b можно заменить на h.
Как вычислить объем фигуры?
Призма представляет собой сравнительной простой полиэдр с высокой симметрией. Поэтому для определения ее объема существует весьма простая формула. Она имеет следующий вид:
V = So*h.
Вычислить площадь основания и высоту может быть сложно, если рассматривается наклонная неправильная фигура. Решается такая задача с помощью последовательного геометрического анализа с привлечением информации о двугранных углах между боковыми параллелограммами и основанием.
Если призма является правильной, тогда формула для V приобретает вполне конкретный вид:
V = n/4*a2*ctg(pi/n)*h.
Как видно, площадь S и объем V для правильной призмы определяются однозначно, если известны два ее линейных параметра.
Призма треугольная правильная
Завершим статью, рассмотрев свойства треугольной призмы правильной. Образована она пятью гранями, три из которых являются прямоугольниками (квадратами), и две - треугольниками равносторонними. Призма имеет шесть вершин и девять ребер. Для этой призмы формулы объема и площади поверхности записаны ниже:
S3 = √3/2*a2 + 3*h*a
V3 = √3/4*a2*h.
Помимо этих свойств, также полезно привести формулу для апофемы основания фигуры, которая представляет собой высоту ha равностороннего треугольника:
ha = √3/2*a.
Боковые стороны призмы - это одинаковые прямоугольники. Длины их диагоналей d равны:
d = √(a2 + h2).
Знание геометрических свойств призмы треугольной представляет не только теоретический, но и практический интерес. Дело в том, что эту фигуру, изготовленную из оптического стекла, применяют для изучения спектра излучения тел.

Проходя через стеклянную призму, свет разлагается на ряд составляющих цветов в результате явления дисперсии, что создает условия для изучения спектрального состава электромагнитного потока.



























