Когда в физике изучают процесс движения тел в неинерциальных системах отсчета, то приходится учитывать так называемое кориолисово ускорение. В статье мы дадим ему определение, покажем, по какой причине оно возникает и где проявляется на Земле.
Что такое кориолисово ускорение?
Если отвечать коротко на этот вопрос, то можно сказать, что это то ускорение, которое возникает в результате действия силы Кориолиса. Последняя проявляет себя, когда тело движется в неинерциальной вращающейся системе отсчета.
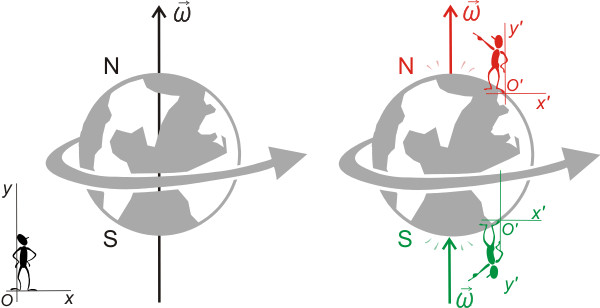
Напомним, что неинерциальные системы движутся с ускорением или вращаются в пространстве. В большинстве физических задач наша планета полагается инерциальной системой отсчета, поскольку ее угловая скорость вращения слишком мала. Однако, при рассмотрении данной темы Земля полагается неинерциальной.
В неинерциальных системах существуют фиктивные силы. С точки зрения наблюдателя, находящегося в неинерциальной системе, эти силы возникают без каких-либо причин. Например, центробежная сила - является ненастоящей. Ее появление вызвано не воздействием на тело, а наличием у него свойства инерции. То же самое относится к силе Кориолиса. Она является фиктивной силой, вызванной инерционными свойства тела во вращающейся системе отсчета. Ее название связано с фамилией француза Гаспара Кориолиса, который впервые ее рассчитал.

Сила Кориолиса и направления движения в пространстве
Познакомившись с определением кориолисова ускорения, рассмотрим теперь конкретный вопрос - при каких направлениях перемещения тела в пространстве относительно вращающейся системы оно возникает.
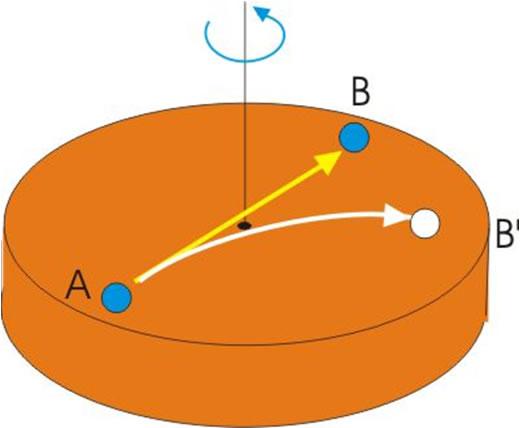
Представим себе вращающийся в горизонтальной плоскости диск. Через его центр проходит вертикальная ось вращения. Пусть на диске относительно него покоится тело. В состоянии покоя на него действует центробежная сила, направленная по радиусу от оси вращения. Если не существует центростремительной силы, которая ей противодействует, то тело слетит с диска.
Теперь предположим, что тело начало двигаться вертикально вверх, то есть параллельно оси. В этом случае его линейная скорость вращения вокруг оси будет равна таковой для скорости диска, то есть никакой кориолисовой силы не будет возникать.
Если тело начало совершать радиальное движение, то есть начало приближаться или удалятся от оси, то появляется сила Кориолиса, которая будет направлена по касательной к направлению вращения диска. Ее появление связано с сохранением момента импульса и с наличием некоторой разности в линейных скоростях точек диска, которые находятся на разном расстоянии от оси вращения.
Наконец, если тело будет перемещаться по касательной к вращающемуся диску, то появится дополнительная сила, которая будет его толкать либо к оси вращения, либо от нее. Это радиальная компонента силы Кориолиса.
Поскольку направление кориолисова ускорения совпадает с направлением действия рассмотренной силы, то это ускорение также будет иметь две компоненты: радиальную и тангенциальную.
Формула силы и ускорения
Сила и ускорение в соответствии со вторым ньютоновским законом связаны друг с другом следующим соотношением:
F = m*a.
Если рассмотреть пример выше с телом и вращающимся диском, то можно получить формулу для каждой компоненты кориолисовой силы. Для этого следует применить закон сохранения углового момента, а также вспомнить формулу для центростремительного ускорения и выражение связи угловой и линейной скорости. В итоге, кориолисова сила может быть определена следующим образом:
F = -2*m*[ω*v].
Здесь m - масса тела, v - его линейная скорость в неинерциальной системе, ω - скорость угловая самой системы отсчета. Соответствующая формула кориолисова ускорения примет вид:
a = -2*[ω*v].
В квадратных скобках стоит векторное произведение скоростей. Оно содержит ответ на вопрос, куда направлено кориолисово ускорение. Его вектор направлен перпендикулярно и оси вращения, и линейной скорости перемещения тела. Это означает, что изучаемое ускорение приводит к искривлению прямолинейной траектории движения.
Влияние силы Кориолиса на полет пушечного ядра

Чтобы лучше понять, как на практике проявляет себя изучаемая сила, рассмотрим следующий пример. Пусть пушка, находясь на нулевом меридиане и нулевой широте, выполняет выстрел строго на север. Если бы Земля не вращалась с запада на восток, то ядро упало бы на долготе 0°. Однако из-за вращения планеты ядро упадет на другой долготе, смещенной к востоку. Это и есть результат действия кориолисова ускорения.
Объяснение описанного эффекта простое. Как известно, точки на поверхности Земли вместе с воздушными массами над ними имеют большую линейную скорость вращения, если они находятся в низких широтах. При вылете из пушки ядро обладало большой линейной скоростью вращения с запада на восток. Эта скорость приводит к его смещению в восточном направлении при полете в более высоких широтах.
Эффект Кориолиса и морские и воздушные течения
Ярче всего влияние силы Кориолиса прослеживается на примере океанских течений и на движении воздушных масс в атмосфере. Так, течение Гольфстрим, начинаясь на юге Северной Америке, пересекает весь Атлантический океан и достигает берегов Европы благодаря отмеченному эффекту.
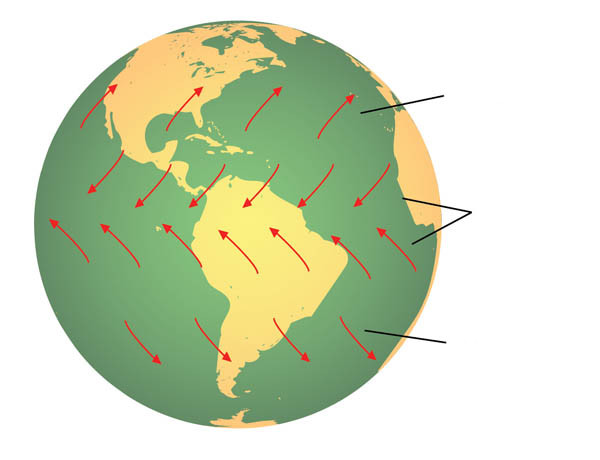
Что касается воздушных масс, то ярким проявлением влияния силы Кориолиса являются ветра пассаты, которые круглый год дуют с востока на запад в низких широтах.
Пример задачи
Выше была записана формула для ускорения Кориолиса. Необходимо с ее использованием вычислить величину ускорения, которое приобретает тело, двигаясь со скоростью 10 м/с, на широте 45°.
Чтобы пользоваться формулой для ускорения применительно к нашей планете, следует добавить в нее зависимость от широты θ. Рабочая формула будет иметь вид:
a = 2*ω*v*sin(θ).
Знак минус был опущен, поскольку он определяет направление ускорения, а не его модуль. Для Земли ω = 7,3*10-5 рад/с. Подставляя все известные числа в формулу, получаем:
a = 2*7,3*10-5*10*sin(45o) = 0,001 м/с2.
Как видно, рассчитанное кориолисово ускорение практически в 10 000 раз меньше ускорения свободного падения.