Чтобы читателю было легче представить себе, что такое гиперболоид - трехмерный объект, - сначала надо рассмотреть одноименную кривую гиперболу, помещающуюся в двумерное пространство.
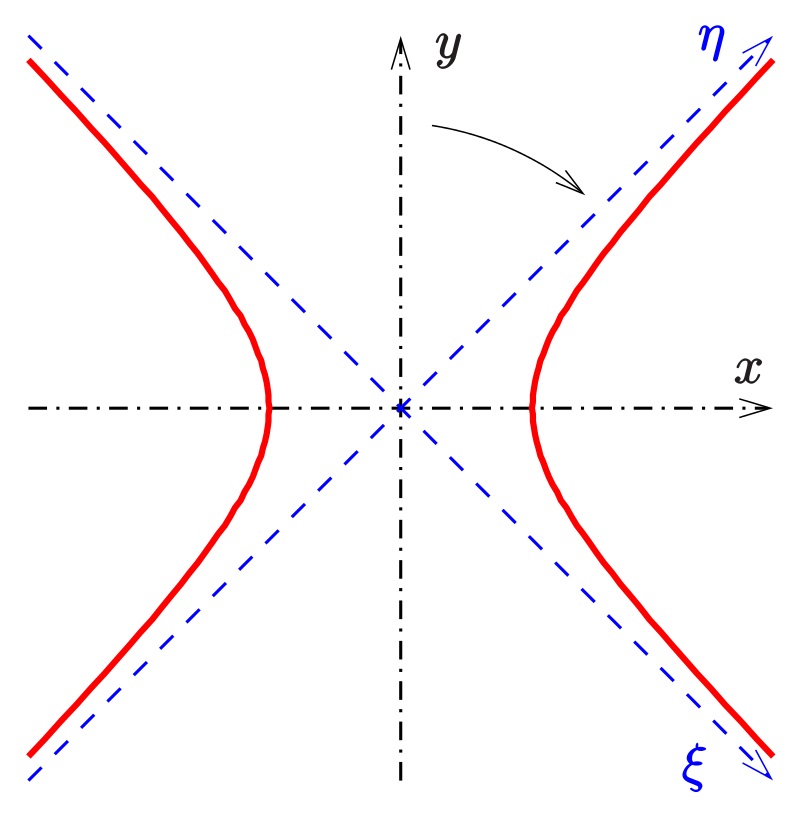
У гиперболы есть две оси: действительная, на данном рисунке совпадающая с осью абсцисс, и мнимая - с осью ординат. Если мысленно начать проворачивать уравнение гиперболы вокруг ее мнимой оси, то поверхность, "заметенная" кривой, составит из себя однополостной гиперболоид.
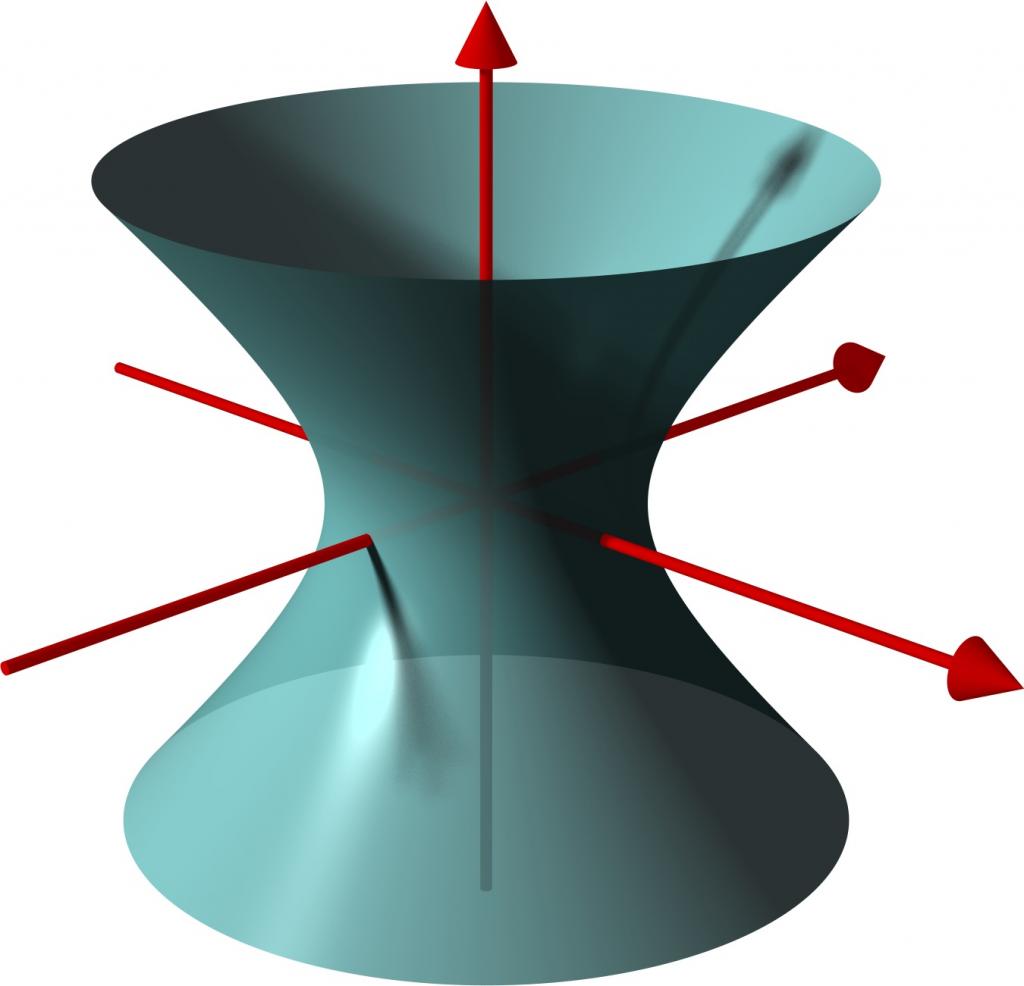
Если же начать вращать таким образом гиперболу вокруг ее действительной оси, то каждая из двух "половинок" кривой составит свою отдельную поверхность, и вместе это будет называться двуполостным гиперболоидом.
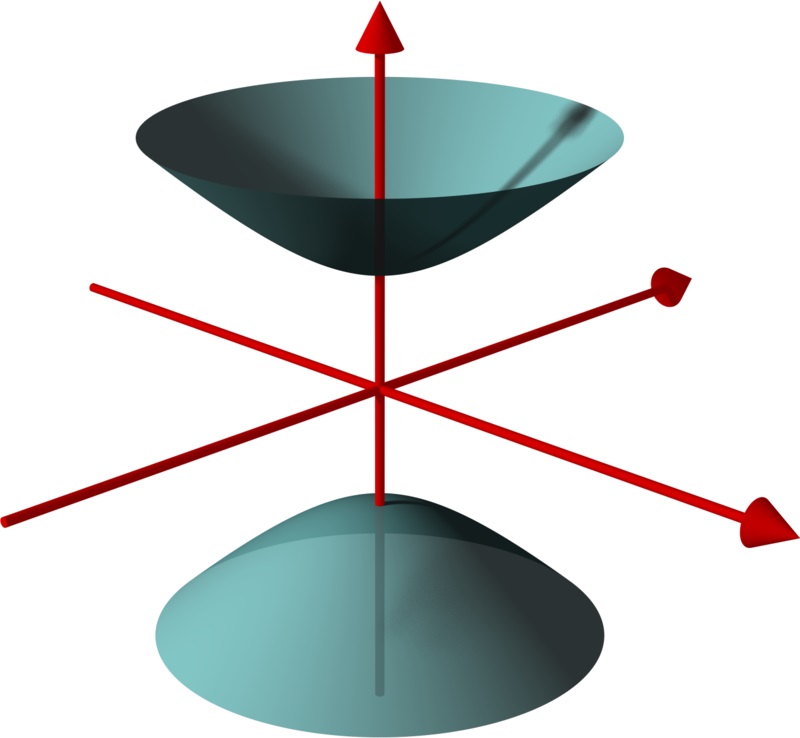
Полученные с помощью вращения соответствующей плоской кривой, они называются соответственно гиперболоидами вращения. У них во всех направлениях, перпендикулярных оси вращения, сохраняются параметры, принадлежащие вращаемой кривой. В общем случае это не так.
Уравнение гиперболоида
В общем случае поверхность может быть задана следующими уравнениями в декартовых координатах(x,y,z):

В случае гиперболоида вращения его симметрия относительно оси, вокруг которой вращали, выражается в равенстве коэффициентов a=b.
Характеристики гиперболоида
У него есть фокус. Мы знаем, что фокусы есть у кривых на плоскости - в случае с гиперболой, например, модуль разности расстояний от произвольной точки, на гиперболе до одного фокуса и второго постоянен по определению, собственно, точек фокуса.
При переходе в трехмерное пространство определение практически не меняется: фокусы - это опять две точки, и разность расстояний от них до произвольной точки, принадлежащей поверхности гиперболоида, постоянна. Как видно, из изменений появилась только третья координата у всех возможных точек, потому что теперь они задаются в пространстве. Вообще говоря, определение фокуса эквивалентно выявлению типа кривой или поверхности: говоря о том, как расположены точки поверхности относительно фокусов, мы фактически отвечаем на вопрос, что такое гиперболоид и как он выглядит.
Стоит вспомнить, что у гиперболы есть асимптоты - прямые, к которым ее ветви стремятся на бесконечности. Если при построении гиперболоида вращения мысленно вращать асимптоты вместе с гиперболой, то кроме гиперболоида получится еще и конус, называемый асимптотическим. Асимптотический конус есть как у однополостных, так и у двуполостных гиперболоидов.
Еще одна важная характеристика, имеющаяся лишь у однополостного гиперболоида, - прямолинейные образующие. Как видно из названия, это линии, и они полностью лежат на заданной поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие. Они принадлежат соответственно двум семействам прямых, которые описываются следующими системами уравнений:
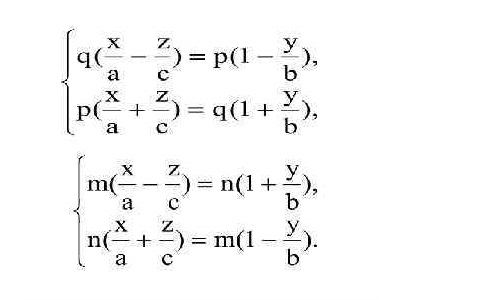
Таким образом, однополостный гиперболоид целиком можно составить из бесконечного числа прямых линий двух семейств, причем каждая линия одного из них будет пересекаться со всеми линиями другого. Поверхности, отвечающие таким свойствам, называются линейчатыми; их можно построить с помощью вращения одной прямой. Определение через взаимное расположение прямых (прямолинейных образующих) в пространстве также может служить однозначным обозначением того, что такое гиперболоид.
Интересные свойства гиперболоида
Кривые второго порядка и соответствующие им поверхности вращения каждая имеют интересные оптические свойства, связанные с фокусами. В случае с гиперболоидом это формулируется следующим образом: если из одного фокуса выпустить луч, то, отразившись от ближайшей "стенки", он примет такое направление, как будто шел из второго фокуса.
Гиперболоиды в жизни
Скорее всего, большинство читателей начинали свое знакомство с аналитической геометрией и поверхностями второго порядка с фантастического романа Алексея Толстого "Гиперболоид инженера Гарина". Однако писатель то ли сам хорошенько не знал, что такое гиперболоид, то ли пожертвовал точностью в угоду художественности: описываемое изобретение по физическим характеристикам скорее является параболоидом, который собирает все лучи в одном фокусе (в то время как оптические свойства гиперболоида связаны с рассеиванием лучей).

В архитектуре очень популярны так называемые гиперболоидные конструкции: это сооружения, по форме являющиеся однополостным гиперболоидом либо гиперболическим параболоидом. Дело в том, что только у этих поверхностей вращения второго порядка есть прямолинейные образующие: таким образом, изогнутую конструкцию можно соорудить только из прямых балок. Достоинства таких конструкций - в способности выдерживать большие нагрузки, например, от ветра: форму гиперболоида используют при строительстве высоких сооружений, например, телевышек.



























