Формула Герона, или Как найти по трем сторонам площадь треугольника

Треугольник является самой простой замкнутой на плоскости фигурой, состоящей всего из трех между собой соединенных отрезков. В задачах по геометрии часто необходимо определить площадь этой фигуры. Что для этого нужно знать? В статье ответим на вопрос, как по трем сторонам найти площадь треугольника.

Общая формула

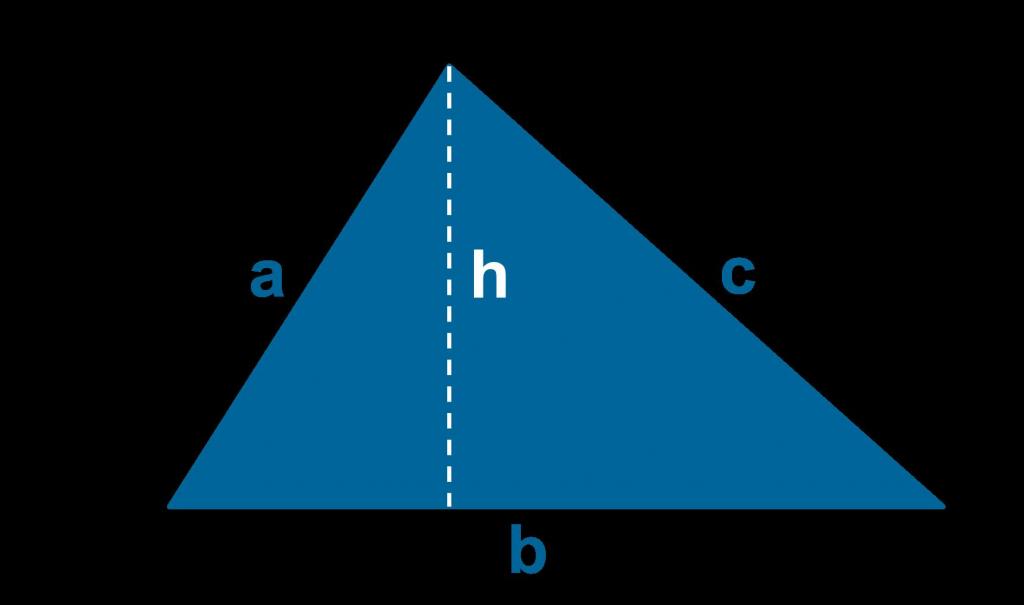
Каждый школьник знает, что площадь треугольника вычисляется как произведение длины любой его стороны - a на половину высоты - h, опущенной на выбранную сторону. Ниже приведена соответствующая формула: S = a*h/2.

Этим выражением можно воспользоваться, если известны хотя бы две стороны и значение угла между ними. В этом случае высоту h несложно рассчитать с использованием тригонометрических функций, например, синуса. Но как найти по трем сторонам треугольника площадь, знает далеко не каждый.

Формула Герона

Именно эта формула является ответом на вопрос, как по трем сторонам найти площадь треугольника. Прежде чем ее записать, обозначим длины отрезков произвольной фигуры как a, b и c. Формула Герона записывается в следующем виде: S = √(p*(p-a)*(p-b)*(p-c)).

Где p - полупериметр фигуры, то есть: p = (a+b+c)/2.

Несмотря на кажущуюся громоздкость, приведенное выражение для площади S запомнить легко. Для этого следует сначала рассчитать полупериметр треугольника, затем вычесть из него по одной длине стороны фигуры, перемножить все полученные разницы и сам полупериметр. В конце следует взять квадратный корень от произведения.

Данная формула носит имя Герона Александрийского, жившего в начале нашей эры. Современная история полагает, что именно этот философ впервые применил указанное выражение для выполнения соответствующих вычислений. Эта формула опубликована в его труде "Метрика", который датируется 60-м годом нашей эры. Отметим, что некоторые работы Архимеда, жившего на два столетия раньше Герона, содержат признаки того, что греческому философу была уже известна формула. Кроме того, как найти площадь треугольника, зная три стороны, также знали древние китайцы.

Важно отметить, что поставленную задачу можно решить, не зная о существовании формулы Герона. Для этого следует провести в треугольнике пару высот и воспользоваться общей формулой из предыдущего пункта, составив соответствующую систему уравнений.

Выражение Герона можно использовать для вычисления площадей произвольных многоугольников, предварительно разбивая их на треугольники и вычисляя длины возникающих диагоналей.

Пример решения задачи

Зная, как по трем сторонам найти площадь треугольника, закрепим полученные знания с помощью решения следующей задачи. Пусть стороны фигуры равны 5 см, 4 см и 3 см. Нужно найти площадь.

Известны три стороны треугольника, значит, можно воспользоваться формулой Герона. Вычисляем полупериметр и необходимые разности, имеем:

• p = (a+b+c)/2 = 6 см;
• p-a = 1 см;
• p-b = 2 см;
• p-c = 3 см.

Тогда получаем площадь: S = √(p*(p-a)*(p-b)*(p-c)) = √(6*1*2*3) = 6 см².

Приведенный в условии задачи треугольник является прямоугольным, что нетрудно проверить, если воспользоваться теоремой Пифагора. Поскольку площадь такого треугольника половине произведения катетов равна, то получаем: S = 4*3/2 = 6 см².

Полученное значение совпадает с аналогичным для формулы Герона, что подтверждает справедливость последней.