Одним из законов гидростатики является правило Архимеда. В статье мы расскажем, что оно собой представляет, выведем его формулу. Рассмотрим, какие силы действуют на тело, когда оно полностью и частично погружено в жидкость. Расскажем историю, которая помогла Архимеду сделать свое знаменитое открытие.
Погружение тела в жидкость
Прежде чем перейти к закону гидростатики, проведем опыт. Мы будем взвешивать тело, например, брусок или кусочек пластилина, с помощью динамометра.

Вес — это сила воздействия тела на подвес или опору. В нашем случае подвес — это крючок динамометра. Цена деления прибора — 0,05 Ньютона (Н). Подвесим тело к нему и увидим по шкале, сколько оно весит. Устройство показывает значение равное 1 Н.
Если динамометр показывает силу в один ньютон, значит, его тянет вверх сила, равная одному ньютону (сила упругости пружины). Обозначим ее буквой F. Тело находится в равновесии, но что уравновешивает F? Сила тяжести. Она приложена к центру тяжести и направлена вниз. Fтяж = F = 1 Н.
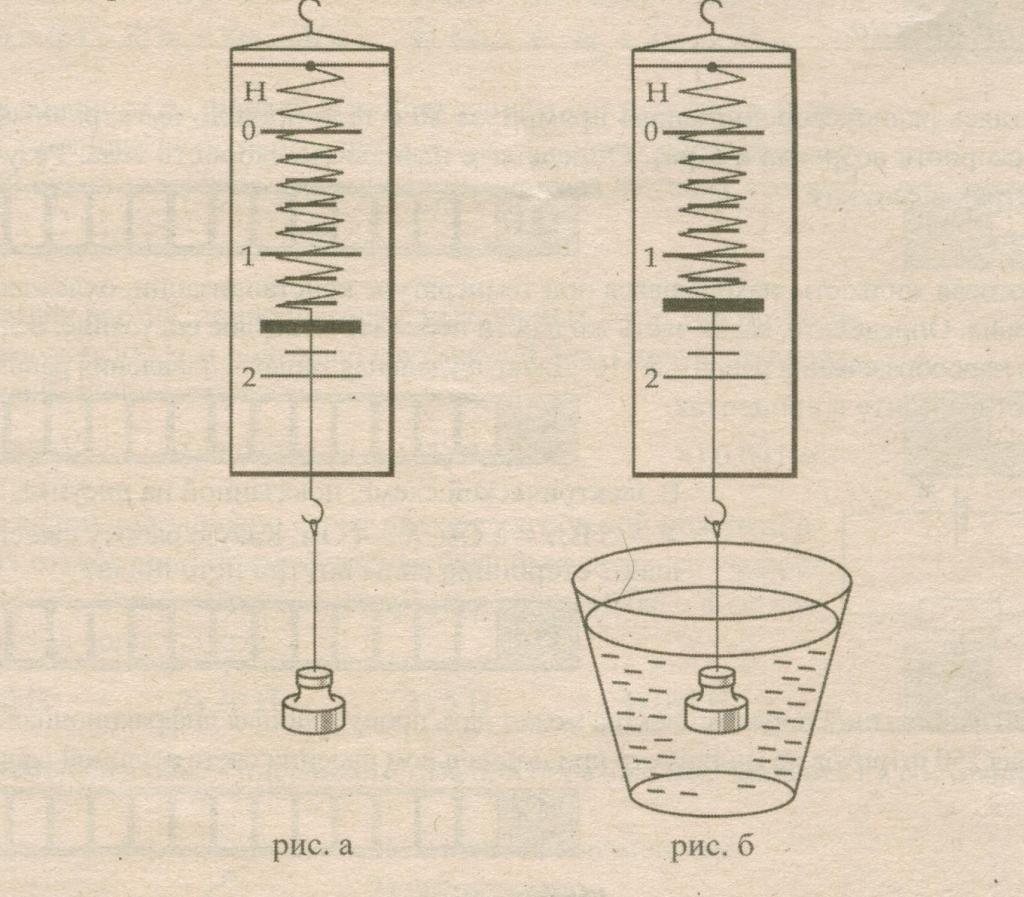
Возьмем стакан воды и будем постепенно погружать в него тело (см. рисунок выше). Что происходит с динамометром? Как только тело лишь коснулось поверхности воды, динамометр уже показывает меньшее значение (до погружения — рисунок а, после — рисунок б). Чем глубже опускается тело, тем меньше становятся показания динамометра. Когда все тело окажется в воде, на шкале прибора мы увидим значение в 0,2 ньютона.
Архимедова сила
Понять закон гидростатики нам поможет схема. Изобразим динамометр и тело в жидкости.
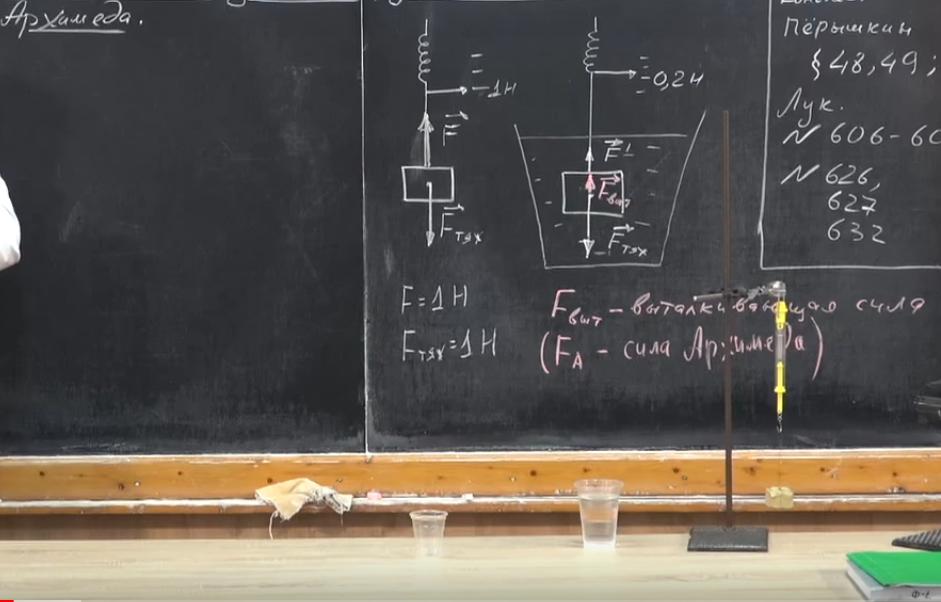
Пружина прибора растягивается, как мы выяснили, силой в 0,2 Н. Обозначим ее F′. Она по-прежнему направлена вверх, потому что пружина динамометра натянута. Когда мы погрузили тело в жидкость, сила тяжести, действующая на него, изменилась? Нет, земля все так же притягивает это тело. Покажем на схеме эту силу с тем же вектором, что и прежде.
А почему тогда показания динамометра уменьшились? Кроме тяготения и упругости пружины, теперь на тело со стороны воды действует направленная вверх выталкивающая сила Fвыт. Ее еще называют архимедовой (FА).
Выясним, чему в нашем случае она равна. Для этого запишем условие равновесия: направленные вверх F′ и Fвыт вместе уравновешиваются силой тяжести Fтяж. F′ + FА = Fтяж. FA = Fтяж - F′. Установим по этой формуле, чему равна сила Архимеда. FA = 1 - 0,2 = 0,8 Н. Мы провели опыт, а теперь объясним, почему так происходит, какова природа этой силы.
Давление в глубине
Представим себе жидкость, в которую полностью погружено тело. В глубине она сжата, там действует давление, которое называется гидростатическим. Его величина зависит от глубины и плотности жидкости. Тело в пространстве занимает какой-то объем. Верхняя его часть находится на меньшей глубине, значит, гидростатическое давление там будет меньше, чем внизу. На нижнюю часть тела оказывается самое большое давление.
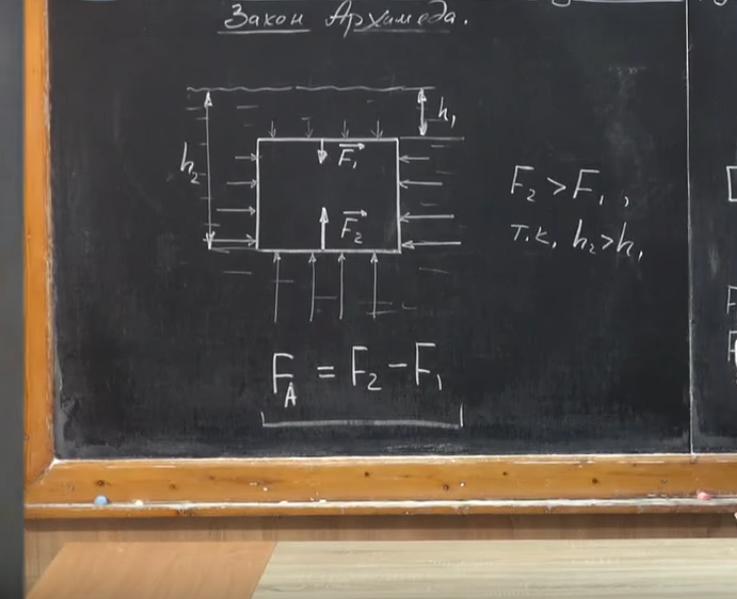
Чтобы найти силу воздействия, надо перемножить давление на площадь поверхности тела. Если сверху давление меньше, то и сила будет мала. Обозначим ее F1. Сила, действующая на нижнюю поверхность, — это F2. F2 > F1, т. к. h2 (глубина на уровне дна бруска) > h1 (глубина нахождения верхней части тела).
На боковые стороны предмета тоже действует силы давления. Но так как они одинаковы и направлены в разные стороны, то компенсируют друг друга. Равнодействующую F1 и F2 можно найти путем вычитания меньшей силы из большей. F = F2 - F1. F направлена вверх, потому что равнодействующая противонаправленных сил всегда имеет такой же вектор что и большая из них. Вывести формулу закона гидростатики будет невозможно без этого понимания.
Равнодействующая F — это есть архимедова сила. FA = F2 - F1. Почему существует выталкивающая сила? С ростом глубины давление жидкости увеличивается. Если взять атмосферное, оно тоже зависит от высоты. Каждые 12 м оно снижается на 1 мм ртутного столба. Именно поэтому воздушный шарик всегда стремится вверх.
Расчет выталкивающей силы
Не только правило Архимеда является одним из основных законов гидростатики. Закон Паскаля тоже относится к их числу. Мы будем использовать его, чтобы вывести формулу для нахождения архимедовой силы в случае, если тело не полностью погружено в жидкость, а частично. Допустим, у нас есть все то же тело в форме прямоугольного параллелепипеда, и оно погружено в жидкость. Площадь основания тела обозначим буквой S, а глубину, на которую погрузили тело, - буквой h. Изобразим схему, которая поможет нам произвести расчет.
Какие силы действуют на тело? Сверху — атмосферное давление. Воздействие обозначим P1. P1 = Pатм. Давление на глубине назовем P2. Чему оно равно? На поверхность жидкости тоже действует атмосферное давление. Если бы его не было, то P2 было бы просто гидростатическим воздействием, которое вычисляется по формуле P=ρ * g * h. Но есть еще атмосферное давление. Закон Паскаля в гидростатике гласит, что воздействие на жидкость передается во все ее точки, причем это происходит без изменения. Атмосферное давление добавляется к гидростатическому. Значит, P2 = Pатм + ρ * g *h.
Теперь мы сможем найти силу давлений. Сверху на тело давит F1, снизу - F2. Равнодействующая этих сил и будет архимедовой. F1 = P1 * S или F1 = Pатм * S. F2 = P2 * S или F2 = (Pатм + ρ * g * h) * S. FA = F2 - F1. Подставляем данные. FA = Pатм * S + ρ * g * h * S - Pатм * S. Сокращаем Pатм * S. Это значит, что не имеет никакого значения, каково атмосферное давление, выталкивающая сила от него не зависит. Но какой показатель важен? Это выражение h * S — объем погруженной части тела. Обозначим его Vпогр.
Опыт Архимеда
Основной закон гидростатики — правило Архимеда: если погрузить тело в жидкость, она вытеснит объем, равный части тела, оказавшейся под поверхностью.
В Греции правил царь Гиерон. Он заказал ювелиру золотую корону, чтобы пожертвовать ее в храм. Отдал мастеру слиток золота, из которого тот изготовил венец. Через время до Гиерона дошли слухи, что ювелир его обманул, заменил часть металла серебром. Царь пригласил Архимеда и попросил его проверить, так ли это.
Архимед, чтобы освежиться, пошел в баню. Надо сказать, что в Древней Греции баня представляла собой не парилку, а ванну, наполненную до краев прохладной водой. Войдя в нее, ученый обратил внимание, что часть жидкости вылилась. Причем чем глубже Архимед погружался, тем больше воды оказывалось на полу. Так было сделано открытие, что количество вытесненной жидкости равно объему погруженного тела. Vпогр = Vвытес.

Архимед провел следующий опыт. Он взял слиток золота такой же массы, как корона, и слиток серебра аналогичного веса. Архимед погружал эти слитки в жидкость. Выяснилось, что серебряный вытесняет больше воды, чем золотой. А когда он погрузил корону той же массы, оказалось, что она вытесняет больше жидкости, чем золотой слиток, но меньше, чем серебряный. Из этого Архимед сделал вывод, что ювелир был нечист на руку и добавил серебро в венец. Он рассказал об этом Гиерону, и тот в качестве награды подарил Архимеду корону. Что было с ювелиром, история умалчивает.
Закон Архимеда
Возвратимся к формуле. Сделав некоторые преобразования, получим FА = ρ * g * Vпогр. Что такое ρ * Vпогр? Это масса вытесненной жидкости. Если мы умножим ее на ускорение свободного падения (ρ * g * Vпогр), то узнаем силу тяжести, действующую на вытесненную жидкость. Но так как последняя неподвижна, то это будет ее вес.
Теперь мы знаем, что сила — это вектор, у которого есть направление. Она направлена вверх. Модуль вектора равен весу вытесненной телом жидкости. На основании этого можно сформулировать закон гидростатики Архимеда: на тело, которое опустили в жидкость, действует сила, равная весу жидкости, вытесненной этим телом. Данное правило еще называется принципом вытеснения.



























