Радиус описанной окружности является важной характеристикой в геометрии. Этот параметр позволяет определить размер и положение окружности относительно данной фигуры или точки.
Рассмотрим подробнее, что представляет собой радиус описанной окружности и как его вычислить в различных ситуациях.
Определение радиуса описанной окружности
Описанной называется окружность, которая проходит через все вершины многоугольника или другой плоской фигуры. При этом центр описанной окружности располагается внутри фигуры.
Радиус такой окружности равен расстоянию от ее центра до любой вершины исходной фигуры. Иными словами, это наибольшее расстояние от центра окружности до стороны фигуры.
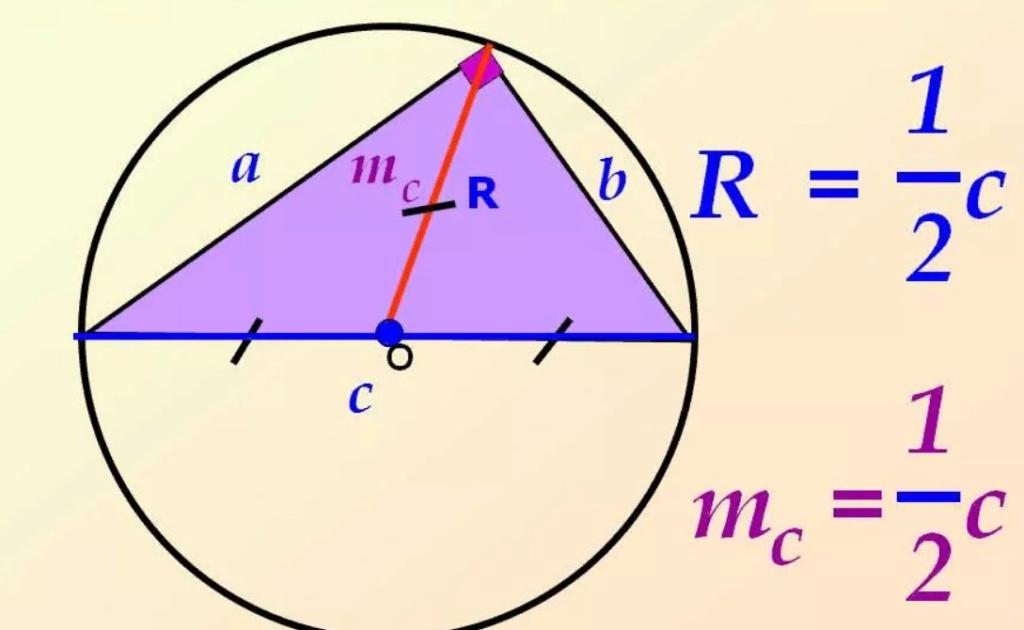
Вычисление радиуса для различных фигур
Для прямоугольника радиус описанной окружности равен полусумме сторон. Формула имеет вид:
R = (AB + CD) / 2,
где AB и CD - стороны прямоугольника.
Для квадрата со стороной a радиус описанной окружности рассчитывается по формуле:
R = a / √2.
Для правильного многоугольника с n сторонами радиус описанной окружности равен:
R = a / (2sin(π/n)),
где a - длина стороны многоугольника.
Применение свойств радиуса описанной окружности
Знание радиуса описанной окружности позволяет решать многие задачи на построение и вычисление.
Например, используя радиус описанной окружности треугольника, можно найти его площадь по формуле:
S = πR^2 cotα,
где α - угол треугольника.
Также радиус описанной окружности применяется при решении задач на разрезание и складывание фигур. Он позволяет определить их взаимное расположение и соотношение размеров.
Зная радиус, можно построить саму описанную окружность, что часто требуется в геометрических построениях. Таким образом, радиус описанной окружности - удобный и важный параметр при работе с плоскими фигурами.
Подводя итог, отметим, что радиус описанной окружности позволяет связать окружность с исходной фигурой. Зная его значение, можно определить взаимное расположение фигур и решить многие геометрические задачи на построение, вычисление площадей, углов и других параметров.

Примеры задач на вычисление радиуса описанной окружности
Для лучшего понимания применения формул вычисления радиуса описанной окружности рассмотрим несколько примеров задач.
Задача 1. Дан прямоугольник со сторонами 10 см и 6 см. Найти радиус описанной окружности.
Решение. По формуле для прямоугольника:
R = (AB + CD) / 2 = (10 + 6) / 2 = 8 см.
Ответ: радиус равен 8 см.
Задача 2. Вокруг квадрата со стороной 8 см описана окружность. Найти ее радиус.
Решение. Подставляем данные в формулу для квадрата:
R = a / √2 = 8 / √2 = 5,66 см.
Ответ: радиус равен 5,66 см.
Свойства касательной к описанной окружности
Рассмотрим некоторые интересные свойства касательной к описанной окружности.
Касательная к описанной окружности треугольника проходит через середину дуги, на которую она опирается. Это свойство часто используется при решении задач на построение касательной.
Если провести касательные к описанной окружности четырехугольника из одной точки, то полученные отрезки будут равны. Это позволяет строить равносторонние трапеции и прямоугольники.
Сумма касательных, проведенных из одной точки к описанной окружности правильного многоугольника, равна нулю. Это свойство используется в доказательствах и при решении уравнений.
Таким образом, касательная к описанной окружности обладает множеством полезных свойств, применение которых расширяет возможности геометрических построений.
Описанные окружности в архитектуре и дизайне
Использование описанных окружностей имеет важное практическое значение в архитектуре и дизайне.
В архитектуре описанные окружности часто применяются при проектировании куполов, арок, сводов. Зная радиус, можно точно рассчитать необходимые размеры конструкции.
В дизайне интерьеров описанные окружности помогают гармонично вписать мебель в помещение, обеспечивая эргономику и комфорт.
Описанные окружности также широко используются при создании предметов быта - ваз, чаш, декоративных изделий. Это позволяет придать им плавные и естественные очертания.
Знание свойств описанных окружностей помогает дизайнерам и архитекторам решать различные профессиональные задачи эстетично и грамотно.























