Косинус - одна из основных тригонометрических функций, широко используемая в математике, физике и других областях науки и техники. Эта функция описывает соотношение между углом в прямоугольном треугольнике и его прилежащим катетом. Понимание косинуса и умение им пользоваться крайне важно для изучения тригонометрии, решения тригонометрических уравнений и неравенств, моделирования волновых процессов и многого другого.
Давайте разберемся, почему косинус - это действительно так важно в математике.
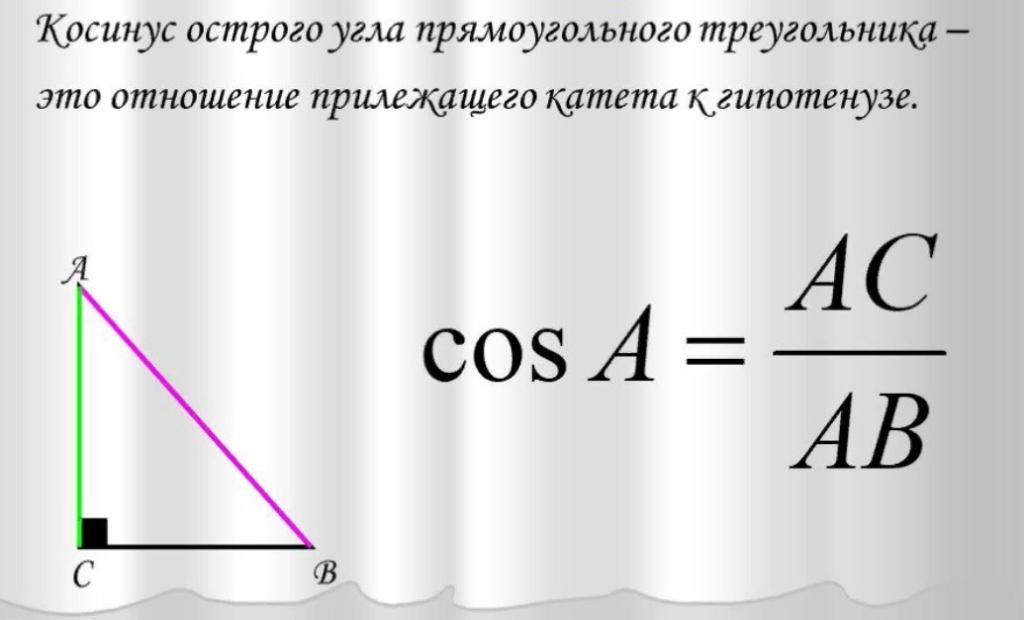
Определение косинуса через отношение сторон треугольника
Косинус угла в прямоугольном треугольнике равен отношению длины прилежащего к этому углу катета к длине гипотенузы. Это фундаментальное определение позволяет вычислять неизвестные элементы треугольника, если известны другие. Благодаря косинусу мы можем находить стороны и углы в треугольниках, что очень полезно в геометрии, тригонометрии и многих прикладных задачах.
Связь с другими тригонометрическими функциями
Косинус тесно связан с синусом и тангенсом угла. Между этими функциями существуют простые соотношения, позволяющие переходить от одной функции к другой. Зная значение косинуса угла, можно найти синус или тангенс того же угла и наоборот. Это дает возможность решать тригонометрические уравнения различными способами.
Таблица косинусов и ее применение
Для углов от 0 до 90 градусов с шагом в 1 градус существуют готовые таблицы значений косинуса. Используя эту таблицу косинусов, можно быстро находить косинус любого из этих углов, не прибегая к вычислениям. Это экономит время при решении задач и позволяет избежать ошибок округления при вычислении косинуса.
Применение косинуса в физике
В физике косинус широко используется для описания гармонических колебаний и волн. С помощью косинуса моделируются синусоидальные сигналы в электротехнике, гармонические колебания в механике, электромагнитные волны в оптике. Без косинуса невозможно было бы изучение переменных токов, колебательных контуров, световых волн.

Применение в инженерных расчетах
При проектировании различных конструкций и сооружений инженеры повсеместно используют косинус для расчета углов, определения размеров элементов, моделирования нагрузок. Например, косинус помогает рассчитать несущую способность ферм, устойчивость опор мостов, прогиб балок и многое другое. Без этой функции современное строительство было бы невозможно.
Таким образом, можно с уверенностью утверждать, что косинус - это действительно одна из ключевых математических функций, имеющая огромное значение в самых разных областях. Знание свойств косинуса и умение оперировать этой функцией является обязательным для математиков, физиков, инженеров и специалистов многих других профессий. Косинус - это то, без чего невозможно представить современную науку и технику.
Вычисление площадей и объемов с помощью косинуса
Косинус также широко используется для вычисления площадей различных геометрических фигур, основанных на треугольниках. Например, площадь трапеции можно найти через основания и угол между ними, используя косинус. Для вычисления объемов тел вращения, таких как цилиндр, конус, шар, применяют интегралы, включающие косинус.
Моделирование сложных периодических процессов
С помощью косинуса можно моделировать гораздо более сложные периодические процессы, чем просто гармонические колебания. Используя разложение функции в ряд Фурье, любой периодический сигнал можно представить как сумму гармоник с косинусами разных частот. Это позволяет анализировать самые разнообразные волновые явления.
Решение тригонометрических уравнений
Косинус играет ключевую роль при решении тригонометрических уравнений. Используя формулы преобразования косинуса суммы и разности аргументов, соотношения между тригонометрическими функциями, свойства четности и нечетности, можно решить тригонометрическое уравнение относительно косинуса.

Применение в вероятности и статистике
В теории вероятностей косинус используется при описании случайных величин, распределенных по нормальному закону. В математической статистике с помощью рядов Фурье, включающих косинусы, осуществляется аппроксимация эмпирических данных. Таким образом, косинус находит применение и в этих областях математики.
Вычисление расстояний и координат с помощью косинуса
Косинус применяется для вычисления расстояний между точками на плоскости и в пространстве через координаты этих точек. Используя теорему косинусов, можно найти неизвестную сторону треугольника и таким образом определить расстояние между объектами. Косинусы позволяют находить координаты точек на плоскости и в пространстве в различных системах координат.
Применение косинуса в оптике
В геометрической оптике косинус угла падения светового луча на границу раздела двух сред равен косинусу угла преломления. Это позволяет рассчитывать ход лучей в линзах и преломление света в различных средах. Косинус также связан с законами отражения света от зеркальных поверхностей.
Методы решения тригонометрических уравнений
Существует множество методов решения тригонометрических уравнений, основанных на свойствах и преобразованиях косинуса: метод разложения на множители, метод замены переменной, графический метод. Косинус позволяет также применять для решения уравнений метод интервалов и метод оценки левой и правой частей.
Обратные тригонометрические функции
На основе косинуса определяется обратная тригонометрическая функция – арккосинус. Он позволяет находить угол по заданному косинусу этого угла. Арккосинус применяется для решения уравнений, нахождения углов и в других задачах.
Косинус в сферической тригонометрии
В сферической геометрии на сфере вместо углов используют дуги больших кругов. Для них определяются тригонометрические функции, в том числе косинус. Это позволяет применять формулы плоской тригонометрии для решения задач на сфере.


























