Таблица квадратов - это уникальный математический инструмент, позволяющий быстро и легко находить квадраты чисел. Но не все знают, как эффективно использовать ее потенциал. В этой статье мы расскажем, как правильно пользоваться таблицей квадратов и извлекать из нее максимум пользы.
Что такое таблица квадратов и зачем она нужна
Таблица квадратов представляет собой своего рода справочник, в котором уже вычислены и сведены воедино квадраты чисел в определенном диапазоне. Обычно таблица содержит квадраты натуральных чисел от 1 до 100 или от 1 до 1000. В ней числа располагаются в порядке возрастания слева направо и сверху вниз. А рядом с каждым числом указан его квадрат.
Например, вот фрагмент таблицы квадратов от 1 до 10:
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Квадрат числа - это число, возведенное в квадрат или умноженное на само себя. Например, \(2^2=2\times 2=4\).
Таблица квадратов позволяет мгновенно находить квадрат любого числа из заданного диапазона. Не нужно каждый раз выполнять умножение в уме или на калькуляторе. Достаточно просто заглянуть в таблицу.
Основные области использования таблицы квадратов:
- Вычисление квадратов чисел
- Решение квадратных уравнений
- Решение задач с применением теоремы Пифагора
- Выполнение других математических операций, требующих возведения в квадрат
Таким образом, таблица квадратов - это очень полезный инструмент, который экономит время и упрощает многие математические вычисления. Поэтому она широко используется как в школе, так и в прикладной математике.
Пошаговая инструкция использования таблицы квадратов
Чтобы эффективно пользоваться таблицей квадратов, нужно знать несколько простых правил.
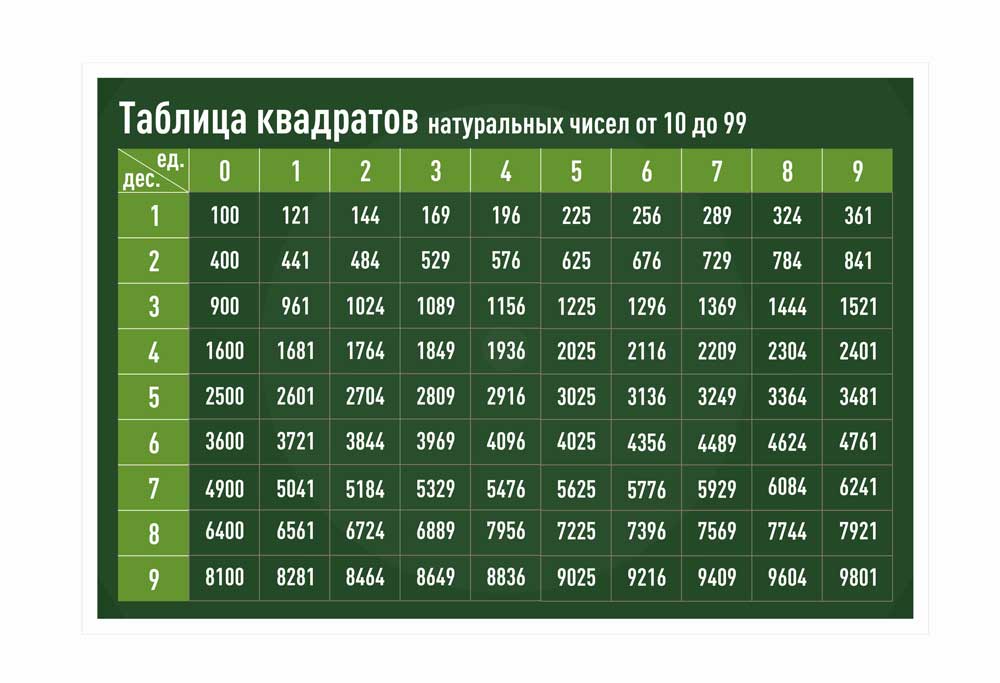
Допустим, нам нужно найти квадрат числа 35. Вот как это сделать:
- Ищем число 35 в первой вертикальной колонке таблицы.
- Ищем число 5 в первой горизонтальной строке.
- Находим пересечение найденных чисел.
- В ячейке пересечения читаем ответ - 1225.
То есть для нахождения квадрата любого двузначного числа нужно найти в таблице его десятки и единицы. А квадрат будет в точке их пересечения.
Этот простой алгоритм позволяет мгновенно вычислять квадраты чисел по таблице, не прибегая к долгим вычислениям. Со временем вы научитесь находить нужные ячейки все быстрее и быстрее.
Главное преимущество таблицы квадратов в том, что она экономит время и избавляет от необходимости запоминать или вычислять квадраты чисел. Достаточно просто уметь пользоваться таблицей!
Конечно, со временем вы можете выучить некоторые базовые квадраты чисел, например от 1 до 10. Но для двузначных и трехзначных чисел таблица будет незаменима.
Давайте теперь разберем несколько конкретных примеров использования таблицы квадратов.
Примеры использования таблицы квадратов для вычисления квадратов чисел
Допустим, нужно найти квадрат числа 48. Ищем число 4 в первом столбце и число 8 в первой строке таблицы. Их пересечение даст нам ответ: 2304.
Еще пример: вычислим квадрат числа 71. В таблице находим число 7 в первом столбце и 1 в первой строке. Квадрат числа 71 равен 5041.
Таким образом, используя таблицу квадратов, можно мгновенно находить квадраты любых двузначных и трехзначных чисел, не прибегая к вычислениям.
Решение квадратных уравнений с помощью таблицы квадратов
Рассмотрим квадратное уравнение вида: x^2 = 25. Чтобы найти x, нужно извлечь квадратный корень из 25. А по таблице квадратов видно, что квадрат числа 5 равен 25. Значит, x = 5.
Другой пример: решим уравнение x^2 = 144. По таблице находим, что 144 - это квадрат числа 12. Следовательно, x = 12.
Так таблица квадратов позволяет быстро находить корни квадратных уравнений, не прибегая к длительным математическим преобразованиям.
Применение таблицы квадратов для решения задач на теорему Пифагора
Одно из распространенных применений таблицы квадратов - решение задач на теорему Пифагора. Например:
В прямоугольном треугольнике один катет равен 3, а другой равен 4. Найдем гипотенузу.
По таблице квадрат 3 равен 9, квадрат 4 равен 16. Их сумма дает 25. Следовательно, квадрат гипотенузы равен 25, а сама гипотенуза - 5.
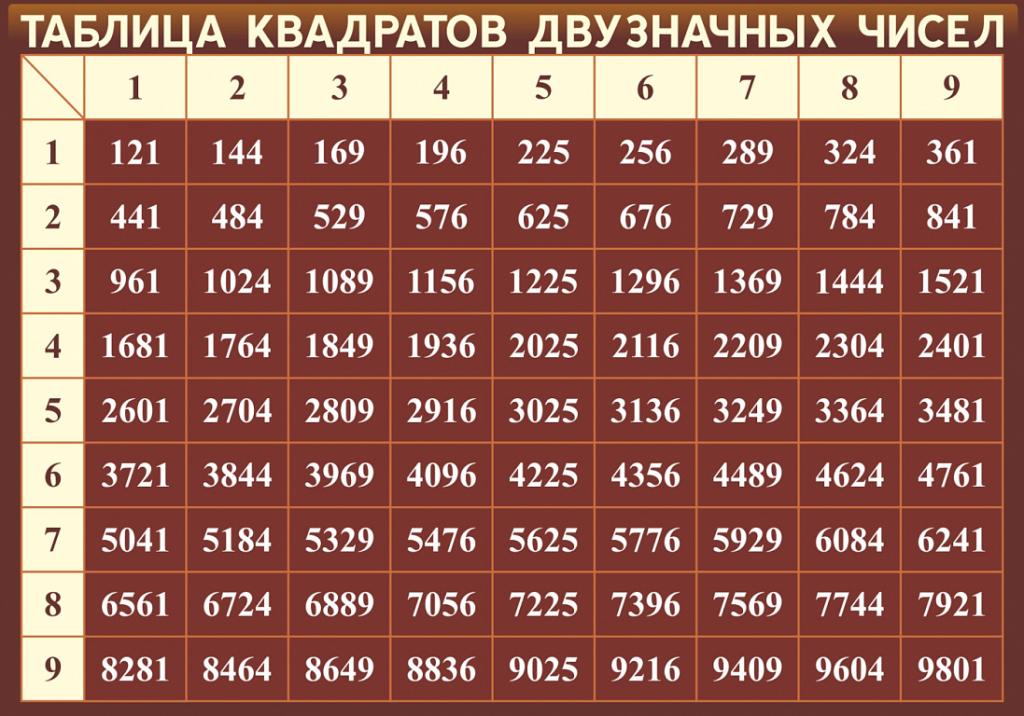
Особенности использования таблицы квадратов для двузначных и трехзначных чисел
При работе с двузначными и трехзначными числами есть несколько нюансов использования таблицы квадратов.
Для двузначных чисел нужно искать пересечение десятков и единиц, как описано выше. А вот для трехзначных чисел следует искать сразу три координаты: сотни, десятки и единицы.
Как избежать типичных ошибок при работе с таблицей квадратов
Чтобы не допускать ошибок при использовании таблицы квадратов, важно быть внимательным и не торопиться. Перед тем как взять число из ячейки пересечения, обязательно дважды проверьте, что нашли правильные координаты.
Также полезно выучить наиболее часто используемые квадраты чисел, чтобы иметь возможность перепроверки. Ну и конечно, регулярно тренируйтесь в использовании таблицы!
Примеры изображений таблицы квадратов
Чтобы лучше понять принцип работы таблицы квадратов, полезно рассмотреть несколько графических примеров.
На этом изображении представлена базовая таблица квадратов для натуральных чисел в диапазоне от 1 до 10. Здесь хорошо видна структура таблицы: числа в первом столбце и первой строке, а их квадраты - в ячейках пересечения.
Таблица квадратов двузначных чисел
На этой таблице показаны квадраты всех двузначных чисел от 10 до 99. Для двузначных чисел нужно находить десятки в первом столбце и единицы в первой строке.
Таблица квадратов трехзначных чисел
Здесь представлен фрагмент таблицы для трехзначных чисел. В этом случае нужно искать сразу три координаты: сотни, десятки и единицы.
Графические примеры помогают лучше разобраться в структуре и принципе работы таблицы квадратов.
























