Подобие треугольников - одна из важнейших тем школьного курса геометрии. В этой статье разберем, что такое подобные треугольники, рассмотрим их свойства и признаки. Пошагово разберем, как доказать подобие треугольников на конкретных примерах.
Основные понятия о подобии треугольников
Два треугольника называются подобными, если их соответствующие углы равны, а соответствующие стороны пропорциональны.
Подобны те треугольники, у которых соответственно равны углы и пропорциональны стороны.
Основные свойства подобных треугольников:
- Соответственные стороны подобных треугольников находятся в одинаковом отношении
- Площади подобных треугольников относятся как квадраты соответствующих сторон
- Соответственные высоты в подобных треугольниках находятся в одинаковом отношении
- Средние линии подобных треугольников находятся в одинаковом отношении
- Радиусы вписанных и описанных окружностей подобных треугольников находятся в одинаковом отношении
Примеры подобных треугольников:
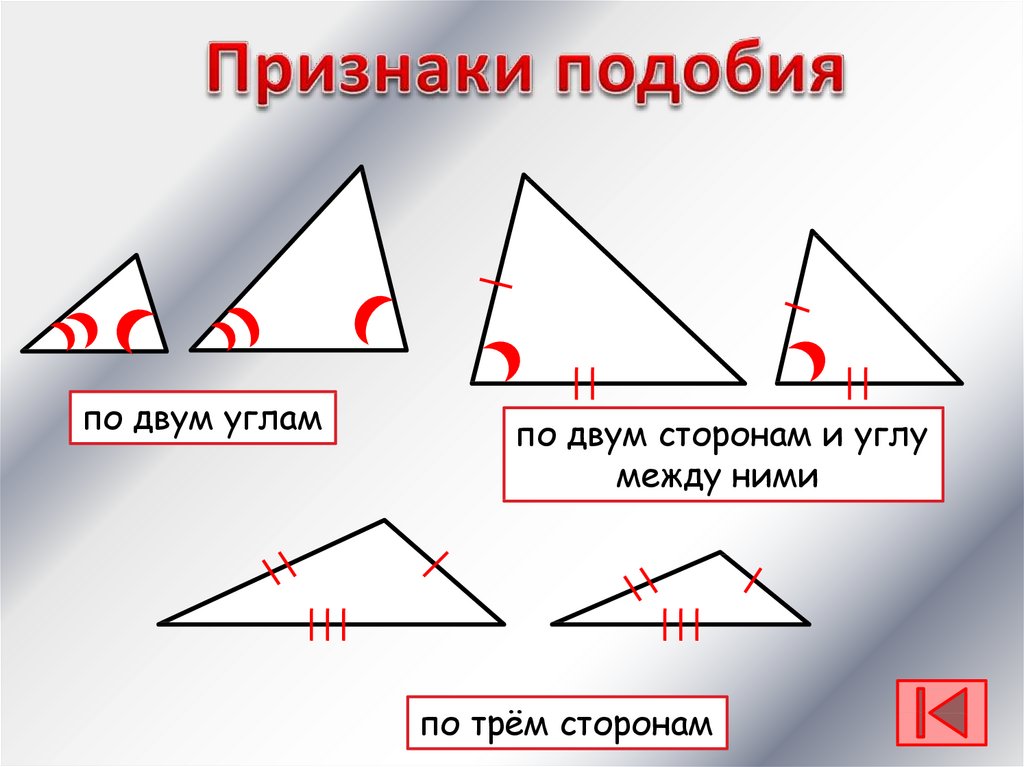
- Треугольники с двумя равными углами
- Треугольники, у которых две стороны пропорциональны, а углы между ними равны
- Треугольники, стороны которых попарно пропорциональны
Коэффициент подобия (k) показывает, во сколько раз одна фигура больше или меньше другой. Его находят как отношение соответствующих сторон подобных треугольников:
k = сторона 1-го треугольника / соответствующая сторона 2-го треугольника
Согласно теореме Фалеса, если две прямые пересекают стороны угла, то они отсекают пропорциональные отрезки на этих сторонах. Это свойство часто используется при доказательстве подобия треугольников.
Изучение подобия треугольников позволяет решать множество геометрических задач на вычисление сторон, углов, площадей. Эти знания применяются в строительстве, архитектуре, дизайне.

Признаки подобия треугольников
Существует 3 основных признака подобия треугольников. Они позволяют доказать, что два произвольных треугольника являются подобными, не вычисляя значения всех элементов.
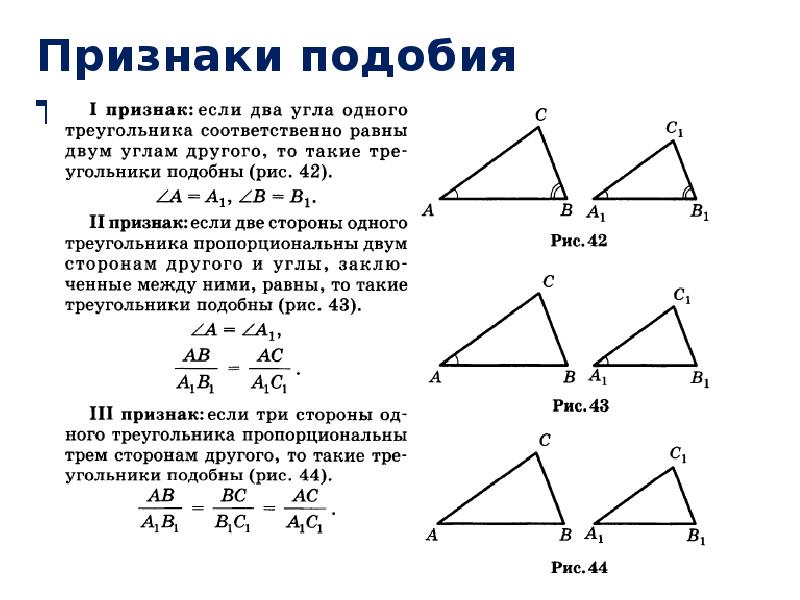
Первый признак подобия треугольников гласит: если два угла одного треугольника равны двум углам другого, то такие треугольники подобны.
Это легко доказать из того, что сумма углов любого треугольника равна 180°. Значит, если два угла равны, то равным будет и третий угол. А раз углы соответственно равны, то треугольники подобны по определению.
Например, рассмотрим треугольники ABC и PQR на рисунке:
| ∠A = 50° | ∠P = 50° |
| ∠B = 70° | ∠Q = 70° |
По первому признаку подобия треугольники ABC и PQR подобны, так как имеют по два равных угла.
Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого, а углы между ними равны, то такие треугольники подобны.
Доказательство этого признака основано на теореме косинусов и тождественных преобразованиях. Рассмотрим применение второго признака на практике:
Даны треугольники ABC и DEF. Известно, что:
- AB = 3 см
- DE = 6 см
- BC = 4 см
- EF = 8 см
- ∠B = ∠E
Проверим соотношения сторон:
AB/DE = 3/6 = 1/2
BC/EF = 4/8 = 1/2
Стороны пропорциональны, углы равны. Значит, по второму признаку треугольники ABC и DEF подобны.
Третий признак подобия треугольника: три стороны одного треугольника пропорциональны трем сторонам другого:
Решение задач на применение признаков подобия треугольников
Рассмотрим несколько примеров задач на применение различных признаков подобия треугольников.
Задача 1. В треугольнике ABC проведена биссектриса AL. Докажите, что треугольник BAL подобен треугольнику ACL.
Решение. Биссектриса делит угол пополам. Значит, ∠BAL = ∠LAC. Кроме того, так как AL - биссектриса, ∠ABL = ∠ACL. Получается, два угла треугольника BAL равны двум углам треугольника ACL. Следовательно, по первому признаку треугольники BAL и ACL подобны.
Задача 2. В равнобедренном треугольнике ABC с основанием AC проведена биссектриса BD. Найдите отношение площадей треугольников ABD и CBD.
Решение. Заметим, что ∠ABD = ∠CBD как вертикальные углы. По первому признаку подобия треугольники ABD и CBD подобны (имеют общий угол CBD и равные углы ABD и CBD).
Сторона AB = BC как стороны равнобедренного треугольника. Тогда отношение площадей подобных треугольников равно квадрату отношения соответствующих сторон (свойство подобных треугольников):
(SABD)/(SCBD) = (AB/CB)2 = 1
Ответ: площади равны.
Рассмотрели лишь несколько задач, чтобы показать применение разных признаков подобия. Как видно из решений, прежде всего нужно определить, какой признак можно использовать из условия задачи, а затем применить его для доказательства подобия треугольников или нахождения отношения их элементов.

Доказательство подобия треугольников в задачах
При решении геометрических задач часто требуется правильно доказать подобие треугольников. Рассмотрим пошаговую методику такого доказательства.
- Проанализировать условие задачи, определить известные и неизвестные элементы треугольников
- Выбрать подходящий признак подобия треугольников, который можно применить к данным треугольникам
- Сформулировать утверждение о подобии треугольников по выбранному признаку
- Обосновать (доказать) справедливость этого утверждения для данных конкретных треугольников
Наглядный пример доказательства для задачи:
Задача. В треугольнике ABC проведены медианы BM и CN таким образом, что отрезок CM параллелен стороне AB. Докажите, что треугольники MBC и ANC подобны.
Решение. Проведенная параллельно стороне прямая отсекает подобный треугольник (свойство) - треугольники ABC и MBC подобны. У них общий угол B и BM параллельна AC (углы равны).
Аналогично треугольники ABC и ANC подобны по тому же свойству: общий угол C, параллельны AN и AB.
У треугольников MBC и ANC угол C является общим. Значит, по первому признаку подобия треугольники MBC и ANC подобны. Что и требовалось доказать.
Доказательство подобия треугольников в задачах
Рассмотрим еще один пример доказательства подобия треугольников для более сложной задачи.
Задача. Дан четырехугольник ABCD. Диагонали его пересекаются в точке O. На сторонах четырехугольника отмечены точки K, L, M и N так, что AK =KD, BL=LC, AM=BM и CN=ND. Докажите подобие треугольников AOM и CNB.
Решение. Заметим, что AK = KD и BL = LC как стороны четырехугольника ABCD. Аналогично AM = BM и CN = ND по условию.
Тогда отношения сторон:
AO/CO = AK/BL (как хорды окружности)
MO/BN = AM/CN (по условию)
Получается, в треугольниках AOM и CNB две пары сторон пропорциональны. При этом ∠OAM = ∠BNC как вертикальные. Значит, треугольники AOM и CNB подобны по второму признаку подобия.
Подобные треугольники в прямоугольных треугольниках
В прямоугольных треугольниках при доказательстве подобия часто используются специальные признаки, вытекающие из свойств прямоугольных треугольников:
- Если в двух прямоугольных треугольниках пропорциональны катеты, то такие треугольники подобны
- Если в двух прямоугольных треугольниках равны острые углы, то такие треугольники подобны
- Если в двух прямоугольных треугольниках пропорциональны гипотенуза и один из катетов, то такие треугольники подобны
Эти утверждения легко доказать, воспользовавшись определением подобных треугольников и свойствами прямоугольных треугольников (теорема Пифагора и соотношения между сторонами и углами).
Типичные ошибки в доказательстве подобия треугольников
Часто в задачах на доказательство подобия треугольников допускаются ошибки:
- Неправильный выбор признака подобия из условия задачи
- Неполное доказательство (например, проверка выполнения лишь части условий признака)
- Использование признаков сходства вместо признаков подобия
- Доказательство равенства элементов треугольников вместо доказательства их подобия
Чтобы избежать таких ошибок, нужно четко представлять отличия сходства и подобия треугольников, а также внимательно анализировать соотношения в условии задачи при выборе признака.
Как научиться доказывать подобие треугольников
Чтобы выработать навык доказательства подобия треугольников, рекомендуется:
- Изучить формулировки всех признаков подобия и запомнить их
- Отработать доказательства признаков подобия
- Решать как можно больше задач на применение разных признаков подобия
- Разобрать типичные ошибки в доказательствах и научиться их избегать
- При решении задач всегда приводить полное строгое доказательство подобия треугольников
Придерживаясь этих рекомендаций и имея достаточную практику, вы сможете свободно доказывать подобие треугольников в любых задачах по геометрии.


























