Ломаные линии - простые на первый взгляд геометрические фигуры. Но если вглядеться пристальнее, они скрывают немало удивительных свойств и тайн. Что же такое ломаная линия? Давайте погрузимся в этот занимательный мир!
1. Определение ломаной линии
В геометрии ломаной линией называют фигуру, состоящую из последовательно соединенных отрезков, в которой конец одного отрезка является началом следующего. Таким образом, основными элементами ломаной являются ее звенья (отрезки) и вершины (концы этих отрезков).
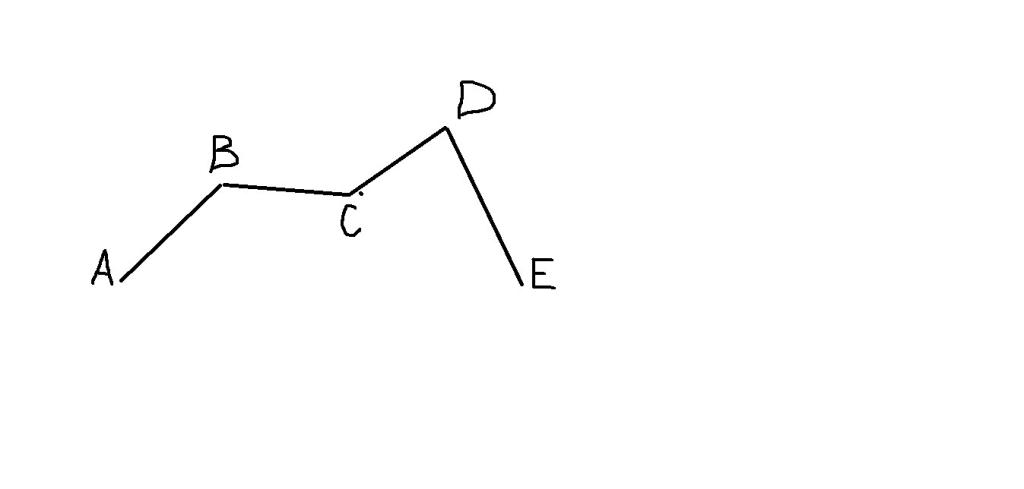
На рисунке изображена ломаная ABCDE, состоящая из звеньев AB, BC, CD, DE и имеющая вершины A, B, C, D, E:
Ломаные линии бывают замкнутыми и незамкнутыми. Замкнутая ломаная - это такая ломаная, у которой совпадают первая и последняя точки. Пример замкнутой ломаной - многоугольник ABCDE на рисунке. А вот ломаная ABCD является незамкнутой, так как ее начальная и конечная точки не совпадают.
Еще один вид ломаных - самопересекающиеся ломаные, у которых некоторые звенья пересекаются между собой. Это может быть как замкнутая, так и незамкнутая ломаная. На рисунке ломаная FGTHK является самопересекающейся, точки F, T, K - точки пересечения ее звеньев.
Таким образом, можно дать следующее определение:
Ломаная линия - геометрическая фигура, состоящая из последовательно соединенных отрезков, в которой конец одного отрезка является началом следующего.
В отличие от ломаной, многоугольник - это замкнутая ломаная, у которой звенья не пересекаются. То есть многоугольник - частный случай ломаной линии.
2. Элементы ломаной линии
Как уже говорилось, основными элементами ломаной линии являются ее звенья и вершины. Давайте подробнее разберемся с их определениями и свойствами.
Звено ломаной - это отрезок, который соединяет соседние вершины ломаной. Конец одного звена является началом другого. У незамкнутой ломаной первое и последнее звенья имеют один свободный конец. А у замкнутой ломаной начало первого звена совпадает с концом последнего.
На примере ломаной ABCDE можно сказать, что звеньями являются отрезки AB, BC, CD и DE. Всего 4 звена.
Вершины ломаной - точки, в которых сходятся соседние звенья. Вершины обозначают заглавными буквами, как правило, в алфавитном порядке.
У ломаной ABCDE вершинами являются точки A, B, C, D и E. Количество вершин всегда на одну больше количества звеньев.
В каждой вершине ломаной образуется угол между сходящимися в ней звеньями. Этот угол может быть как острым, прямым, так и тупым. Например, в вершине B угол между звеньями AB и BC - острый.
Если ломаная является самопересекающейся, то в ней появляются дополнительные особые точки - точки пересечения звеньев. Это те точки, в которых одно звено пересекает другое. На рисунке это точки F, T и K. В отличие от обычных вершин, в точках пересечения углы не образуются.
3. Параметры ломаной линии
Рассмотрим основные параметры, которые можно вычислить для ломаной линии.
Важнейшим параметром любой ломаной является ее длина. Длина ломаной равна сумме длин всех ее звеньев:
где l1, l2,...ln - длины звеньев ломаной.
Например, для ломаной ABCDE, изображенной выше, имеем: l(ABCDE) = l(AB) + l(BC) + l(CD) + l(DE)
Если ломаная замкнутая и не имеет самопересечений, то есть является многоугольником, то ее длина называется периметром этого многоугольника.
Для многоугольников можно также вычислить площадь. Существуют разные формулы для нахождения площадей многоугольников в зависимости от их вида.
4. Построение ломаной линии
Для построения ломаной линии используют такие чертежные инструменты, как линейка, угольник, циркуль, транспортир.
Порядок построения зависит от того, что такое ломаная линия - замкнутая она или нет, и от того, заданы ли длины ее звеньев или углы между ними.
5. Применение ломаных линий
Ломаные линии часто применяются в геометрии для описания формы различных фигур или геометрических тел. Например, грани многогранников представляют собой многоугольники.
На картах местности ломаные используют для обозначения контуров участков, водоемов, дорог и т.д. Таким образом упрощается их описание.
6. Задачи на ломаные линии
Существует множество разных задач, связанных с ломаными линиями. Это могут быть задачи на вычисление параметров ломаной, таких как длина, периметр или площадь.
Также встречаются задачи на построение ломаной с заданными свойствами или нахождение углов, образованных звеньями в вершинах ломаной.
Пример задачи:
Найти периметр ломаной АВСДЕ, если АВ=3 см, ВС=5 см, CD=2 см, DE=4 см.
Решение: Периметр ломаной равен сумме длин всех ее звеньев. В данном случае это будет: P(ABCDE) = AB + BC + CD + DE = 3 см + 5 см + 2 см + 4 см = 14 см
Таким образом, периметр ломаной АВСДЕ равен 14 см.

7. Интересные факты о ломаных
Мир ломаных линий полон удивительных парадоксов и загадок. Например, существует задача про так называемую "ломаную длины 1", у которой при бесконечном количестве звеньев длина все равно конечна и равна 1.
Также ломаные часто используются в различных оптических иллюзиях. Например, есть иллюзия ломаной, которая выглядит, как две разные по длине ломаные, но на самом деле они равны.

8. Ломаные линии в архитектуре
Ломаные линии часто встречаются в архитектуре при проектировании зданий и сооружений. Например, мансардные крыши имеют сломанную двускатную форму.
Также в архитектурных стилях модерн и деконструктивизм применяются нестандартные ломаные линии фасадов и интерьеров зданий. Это придает им выразительность и динамичность.
9. Ломаные линии в природе
Что такое ломаная линия в природе? Это могут быть извилистые очертания рек, берегов морей, горные хребты со множеством вершин и перевалов. Такие природные объекты удобно моделировать с помощью ломаных линий.
Например, при создании географических и топографических карт горные хребты часто изображаются в виде ломаных линий, соединяющих вершины гор.
10. Ломаные в искусстве
В изобразительном искусстве ломаные линии тоже применяются довольно часто. Особенно в таких авангардистских направлениях, как кубизм, футуризм, супрематизм.
Художники используют ломаные формы для передачи динамики, скорости, энергии в своих абстрактных композициях. Также ломаные можно встретить в орнаментах, плакатах, полиграфическом дизайне.


























