Дуга окружности является важным элементом любого круга или окружности. Она задает форму кривой линии и определяет многие свойства окружности. В этой статье мы подробно разберем, что представляет собой дуга, как ее построить, вычислить длину и где применяется на практике.
Определение и обозначение дуги окружности
Дуга окружности - это часть окружности, заключенная между двумя ее точками. Математически дугу определяют как подмножество точек окружности, лежащих между двумя заданными на ней точками A и B.
Любые две точки делят окружность на две дуги.
Геометрически дуга выглядит как отрезок кривой линии окружности. Чтобы отличать две дуги, образованные двумя точками A и B, к каждой добавляют еще по одной точке. Таким образом получаем обозначения ACB и ADB для двух дуг:
На практике дуги встречаются во многих объектах - арках, колесах, куполах зданий и т.д. Они придают конструкциям нужную форму.
Виды дуг окружности
Существует несколько разновидностей дуг:
- Полуокружность - дуга, соответствующая углу 180 градусов
- Меньшая дуга - менее 180 градусов
- Большая дуга - более 180 градусов
- Центральная дуга - опирается на центральный угол
- Дополнительная дуга - вместе с другой дугой охватывает всю окружность
Каждая дуга тесно связана с радиусом и хордой окружности. От радиуса зависит длина дуги, а хорда помогает ее вычислить. Разные дуги используются в зависимости от решаемых задач.
| Тип дуги | Применение |
| Полуокружность | Арки, колеса |
| Меньшая дуга | Детали машин |
Таким образом, вид дуги определяется ее свойствами и назначением в конкретной конструкции.

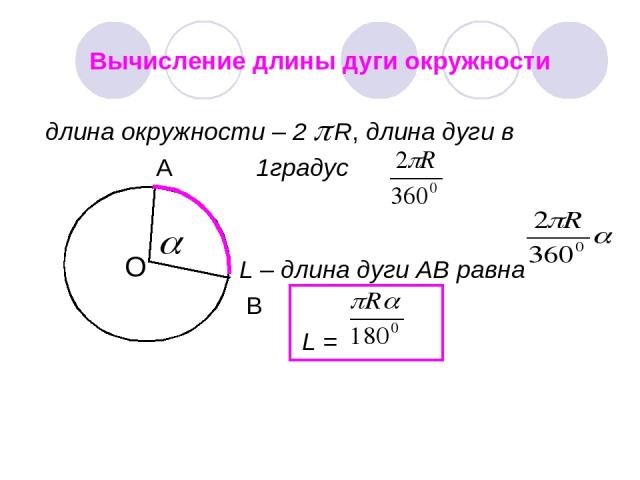
Существует 2 формулы длины дуги окружности:
1) Если дан центральный угол в радианах:l = R*α, где R - радиус, α - величина угла AOB в радианах.
2) Если дан центральный угол в градусах: l = R*π*C/180, где R - радиус, C - величина угла AOB в градусах.
Пример Дано: 1) радиус окружности R = 6 дм. 2) центральный угол AOB = 45°. Найти: Длину дуги AB. Решение: l = 6*3,14*1/4 дм.= 4,71 дм.
Из формулы видно, что длина дуги прямо пропорциональна радиусу. Чем больше радиус, тем длиннее дуга при одном и том же центральном угле.
Давайте вычислим длину дуги конкретного примера:
- Задаем исходные данные: R = 5 см, φ = 60°
- Переводим 60° в радианы: 60° = π/3 радиан
- Подставляем в формулу: L = 5 * (π/3) = 5π/3 см
Пошагово разобрав пример, мы научились находить длину любой заданной дуги окружности.
Применение дуги окружности
Важно: дуги окружности широко используются на практике благодаря своим уникальным свойствам. Рассмотрим основные области применения.
Строительство
В архитектуре дуга окружности часто используется при возведении арок, куполов, сводов. Арки придают зданиям устойчивость и красоту. Дуга окружности это идеальная форма для перекрытия проемов.

Машиностроение
Многие детали машин имеют форму дуги: шестерни, зубчатые колеса, кулачки. Дуга позволяет передавать вращение от одной детали к другой. Также дуги применяются в конструкции автомобильных колес.
Искусство и дизайн
В орнаментах часто встречаются элементы в виде дуг окружности. Они придают композициям гармоничность. Дуга украшает интерьеры, одежду, посуду.

Рекомендации по применению
Чтобы правильно использовать дугу окружности, следует:
- Определить нужный радиус и центральный угол
- Рассчитать длину дуги по формуле
- Построить дугу с помощью циркуля или компьютерной программы
Помните, что от радиуса зависит длина дуги. Увеличивая радиус при одном и том же угле, мы удлиняем дугу.
Как построить дугу окружности
Для построения дуги окружности потребуется:
- циркуль
- линейка
- карандаш
Последовательность действий:
- Найти центр окружности
- Воткнуть ножку циркуля в эту точку
- Другой ножкой начертить дугу нужной длины
Современные графические пакеты также позволяют легко строить дугу окружности заданных параметров.
Выбор оптимальной дуги
При выборе дуги для конкретного применения оптимальным решением будет та дуга, которая:
- обеспечит конструкции нужную форму и размер
- будет прочной и надежной при эксплуатации
- позволит эффективно использовать материал и снизить затраты
Учитывая эти критерии, можно подобрать идеальный вариант дуги для любых целей.
Особенности расчета длины дуги
При вычислении длины дуги окружности существует несколько нюансов, на которые следует обратить внимание.
Единицы измерения угла
Центральный угол в формуле для вычисления длины задается в радианах. Если изначально угол задан в градусах, его нужно конвертировать: 1° = π/180 радиан.
Знак угла
Если центральный угол отрицательный, то при подстановке в формулу его нужно брать по модулю - т.е. без учета знака минус.
Длина и центральный угол
Одинаковые по длине дуги могут соответствовать разным центральным углам в зависимости от радиуса окружности.
Погрешности при построении дуги
На практике получить идеальную дугу бывает сложно. Рассмотрим типичные погрешности.
Неточное определение центра
Если центр найден неверно, дуга будет иметь искаженную форму.
Колебания циркуля
При построении циркулем трудно удержать одинаковый радиус по всей дуге. В результате получаются отклонения.
Ошибки округления
При расчетах на компьютере возникают погрешности из-за округления, которые влияют на точность построения дуги.
Альтернативы дуге окружности
В некоторых случаях вместо дуг можно использовать другие кривые.
Эллиптическая дуга
Обладает вытянутой формой, подходит если нужно создать овальный проем.
Параболическая дуга
Используется в антеннах, отражателях для фокусировки сигнала.



























