Геометрические характеристики сечения играют важную роль в расчетах на прочность и жесткость элементов конструкций. Одной из таких величин является статический момент сечения. Давайте разберемся, что это такое, как его вычислить и где применяют на практике.
Сущность статического момента сечения
Статический момент сечения относительно некоторой оси - это величина, равная сумме произведений элементарных площадок сечения df на их расстояние y до данной оси:
S = ∫ydf
Эта характеристика показывает действие момента сил тяжести стержня относительно выбранной оси координат. Величина статического момента зависит от положения оси и имеет размерность длины в кубе (см3). Она может быть как положительной, так и отрицательной, а также равной нулю.
Статический момент сечения связан с координатами центра тяжести сечения. Если ось проходит через центр тяжести, статический момент будет равен нулю. Это справедливо для любой фигуры.

Например, для прямоугольника со сторонами a и b статический момент относительно оси Х, проходящей через середину стороны a, равен:
S = \dfrac{ab^2}{4}
А для круга радиусом R относительно оси, совпадающей с диаметром:
S = 0
Так как эта ось проходит через центр тяжести круга.
Вывод формулы статического момента сечения
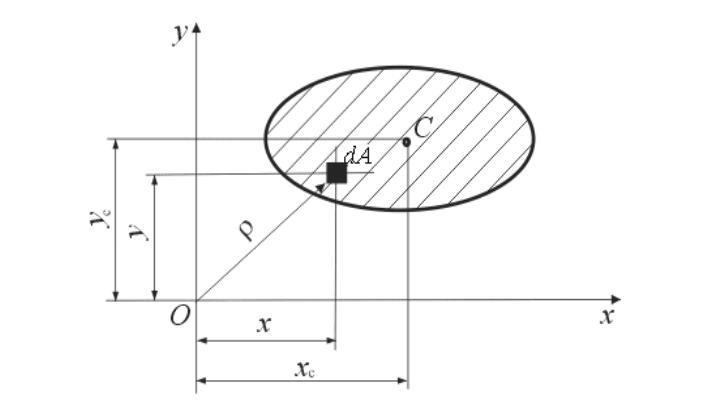
Для произвольной фигуры статический момент сечения можно найти, разбив ее на бесконечно малые элементарные площадки df. Каждая такая площадка умножается на свое плечо - расстояние y до заданной оси. Суммирование таких произведений по всему сечению дает интеграл:
S = ∫ydf
Это и есть общая формула статического момента сечения относительно произвольной оси. При наличии осей симметрии или центра тяжести вычисления могут быть упрощены. Например, для прямоугольника аналитически интегрируя эту формулу, получаем тот же результат:
S = \dfrac{ab^2}{4}
То есть статический момент равен площади сечения, умноженной на расстояние от ее центра тяжести до оси. Этим свойством часто пользуются на практике.
Для более сложных фигур вывод формул требует интегрирования. Например, пусть есть сечение в виде полукруга радиусом R. Тогда относительно оси X, касательной к окружности в точке Y=R, статический момент сечения будет равен:
Для полукруга радиусом R статический момент относительно касательной оси X, проходящей через точку Y=R, равен:
S = \dfrac{\pi R^3}{4}
Вычисление для сечения треугольной формы
Рассмотрим вывод формулы статического момента для поперечного сечения в виде равнобедренного треугольника с основанием а и высотой h относительно оси X, проходящей через вершину:
Разобьем поперечное сечение на узкие полоски параллельные основанию. Высота каждой полоски будет уменьшаться от h до 0. Тогда элементарная площадь df=bdy, а расстояние до оси X определяется координатой y.
Подставляя это в общую формулу статического момента и интегрируя от 0 до h, получаем:
S = \int_0^h ybdy = \dfrac{abh^2}{3}
Учет несимметричных фигур
Если поперечное сечение несимметрично относительно выбранной оси, вычисления усложняются. Например, для трапеции с основаниями a и b и высотой h статический момент относительно оси X, проходящей через середину основания a, будет равен:
S = \dfrac{h(a+b)(a+2b)}{12}
Статический момент для тонкостенных профилей
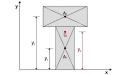
Особенности возникают при вычислении статического момента для тонкостенных профилей, например швеллеров или двутавров. Несмотря на сложную форму, часто можно применить упрощения. Рассмотрим статический момент двутаврового сечения относительно оси Y. Будем считать, что толщина стенки мала по сравнению с размерами полок. Тогда вклад стенки в статический момент пренебрежимо мал и им можно пренебречь. А полки представляют собой два прямоугольника, моменты которых легко посчитать и сложить:
S = S1 + S2
Сравнение значений для разных осей
Цтатические моменты одного и того же сечения заметно отличаются для разных осей. Так для прямоугольника со сторонами a и b:
- Относительно центральной оси Z: S = 0
- Относительно оси X, параллельной стороне a: S = \dfrac{ab^2}{4}
- Относительно оси Y, параллельной стороне b: S = \dfrac{ba^2}{4}
Как видно, статический момент зависит не только от формы сечения, но и от положения выбранной оси.
Применение для расчета касательных напряжений
Одно из основных применений статического момента сечения - это расчет касательных напряжений в поперечных сечениях изгибаемого стержня. Согласно теории сопротивления материалов, касательные напряжения τ в сечении определяются по формуле:
τ = \dfrac{MS}{I}
где M - изгибающий момент в рассматриваемом сечении, S - статический момент части сечения относительно нейтральной оси, I - момент инерции сечения.
Таким образом, зная M, I и вычислив S, можно определить касательные напряжения в любой точке поперечного сечения.
Нахождение положения нейтральной оси
Связь статического момента сечения с координатами центра тяжести позволяет использовать его для нахождения положения нейтральной оси в поперечном сечении изгибаемого элемента. Из уравнений равновесия следует, что центр тяжести сечения и нейтральная ось при чистом изгибе совпадают. Зная статические моменты, можно найти координаты центра тяжести, а значит и положение нейтральной оси относительно какой-либо из осей сечения.
Влияние на несущую способность сечения
При расчете изгибаемых элементов на прочность используется известное соотношение:
M ≤ [σ]WI
где [σ] - допускаемое напряжение материала, W - момент сопротивления сечения.
Очевидно, что с увеличением статического момента сечения возрастают касательные напряжения. А это приводит к снижению запаса прочности сечения и его несущей способности. Поэтому при конструировании стараются минимизировать S, например, располагая сечение симметрично нагрузке.
Расчет прогиба изгибаемого элемента
Статический момент сечения также влияет на жесткость элемента и его прогиб при изгибе. Из теории известна формула для определения прогиба в центре пролета балки:
f = \dfrac{ML^2}{48EI}
Здесь EI - изгибная жесткость балки, которая тем выше, чем больше момент инерции сечения I. Следовательно, минимизируя статический момент S (например, центрируя сечение), можно увеличить I и снизить прогиб элемента.