Вычисление объемов усеченных конусов находит широкое применение в самых разных областях. Это связано с тем, что многие технические объекты, архитектурные сооружения или емкости имеют форму, близкую к усеченному конусу. Зная радиусы оснований и высоту такого конуса, а также формулы для расчета его объема, можно решать важные практические задачи.
- В строительстве и архитектуре при возведении различных конструкций, например башен, мостов и т.д. Это позволяет точно рассчитать расход материалов.
- В машиностроении и приборостроении для определения объемов деталей и узлов.
- В производстве тары и упаковки - банок, бутылок, контейнеров и т.п.
Объемы усеченного конуса могут пригодиться в любой отрасли, где используются подобные геометрические фигуры. Зная радиусы оснований и высоту, расчет объема конуса усеченного позволяет быстро получить необходимый результат.

Особенности применения формулы объема конуса усеченного
Хотя формула объема конуса усеченного довольно проста, при практических расчетах нужно учитывать некоторые нюансы:
- Радиус большего основания R должен быть больше радиуса меньшего основания r. В противном случае речь уже не идет об усеченном конусе.
- Значения радиусов и высоты должны быть положительными величинами.
- Необходимо использовать одинаковые единицы измерения для всех параметров (сантиметры, метры и т.д.).
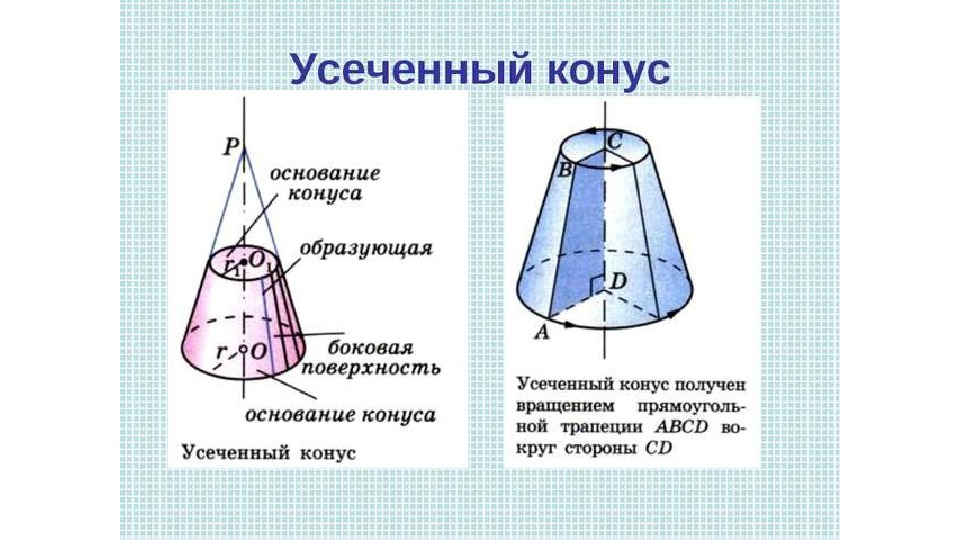
Онлайн калькуляторы объема усеченного конуса
Чтобы упростить вычисления с использованием формулы, существуют удобные онлайн сервисы - калькуляторы объема усеченного конуса. Они позволяют ввести исходные данные в специальные поля и мгновенно получить результат.
Преимущества таких калькуляторов:
- Простота и удобство использования
- Возможность быстро пересчитать при изменении параметров
- Минимизация ошибок при ручных вычислениях
3D модели усеченного конуса
Для наглядности и более глубокого понимания формы усеченного конуса полезно построить его 3D модель с помощью специальных компьютерных программ.
Это позволяет:
- Увидеть конус в объеме и с разных ракурсов
- Легче представлять процессы, связанные с этой фигурой
- Проверить правильность полученных ранее расчетов
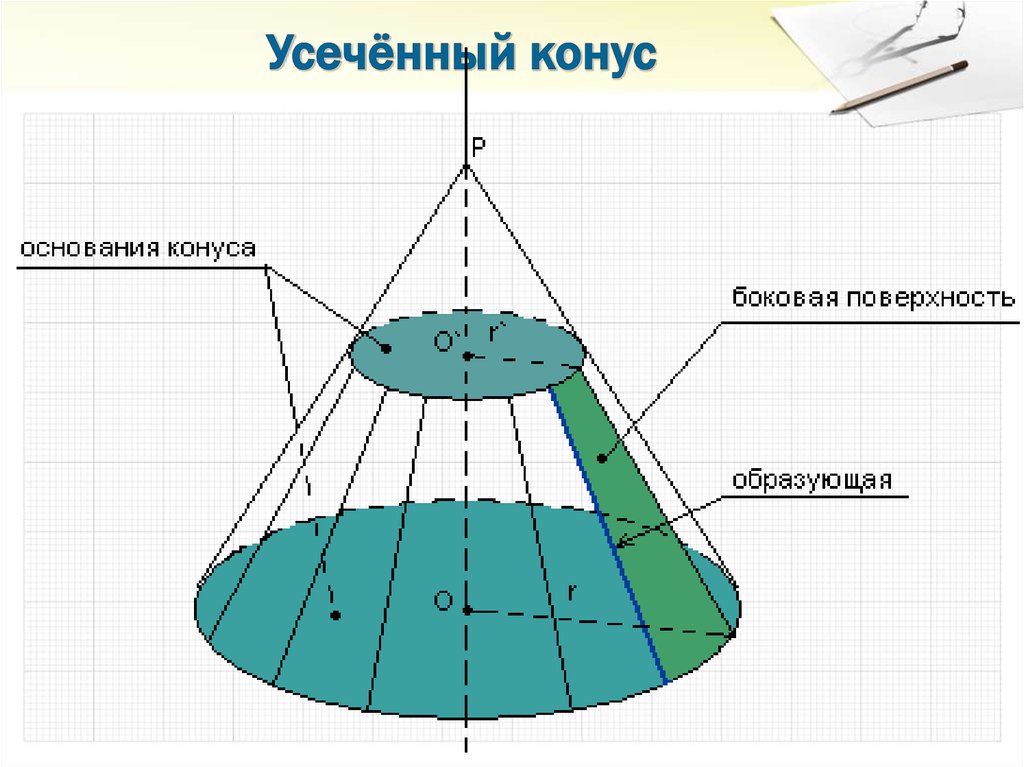
Задачи на вычисление объемов конуса усеченного
Для лучшего усвоения материала полезно решить несколько практических задач на вычисление объема конуса усеченного, используя соответствующую формулу.
Например:
- Дан усеченный конус с R = 5 см, r = 2 см, h = 12 см. Найдите его объем.
- Требуется определить объем металлической емкости в форме усеченного конуса с параметрами: R = 50 см, r = 20 см, h = 30 см.

Пошаговое решение задачи на вычисление объема конуса усеченного
Давайте разберем решение задачи на вычисление объема усеченного конуса по шагам:
- Внимательно прочитать условие и выделить исходные данные - высоту конуса (h), радиус большего основания (R) и радиус меньшего основания (r).
- Записать условие в виде чертежа или схемы, если это возможно. Наглядное представление задачи облегчает дальнейшее решение.
- Вспомнить и записать формулу для вычисления объема усеченного конуса:
V = (π∙h∙(R2 + R∙r + r2))/3
- Подставить числовые значения R, r и h в формулу.
- Выполнить вычисления и найти значение объема V.
- Записать ответ с указанием соответствующих величин и единиц измерения.
- Проверить правильность решения, например, с помощью онлайн калькуляторов.
Анализ реальных объектов формы усеченного конуса
Полезно проанализировать реальные объекты, имеющие форму, близкую к усеченному конусу, и определить их основные параметры.
Это могут быть:
- Архитектурные сооружения (башни, минареты, колокольни)
- Детали машин и механизмов
- Корпуса громкоговорителей, мегафонов
- Банки, бутылки, бочки, воронки
- Крыльчатки насосов и мешалок

3D-печать моделей усеченного конуса
Современные технологии 3D-печати позволяют создавать объемные модели усеченного конуса на основе его цифрового представления.
Это дает возможность наглядно:
- Изучать свойства этой фигуры
- Демонстрировать принципы вычисления объема
- Тестировать точность полученных ранее расчетов


























