Точка пересечения медиан треугольника - удивительное геометрическое свойство, которое на первый взгляд кажется незначительным, но таит в себе массу интересных фактов и практических применений.
Что такое медиана и как ее построить
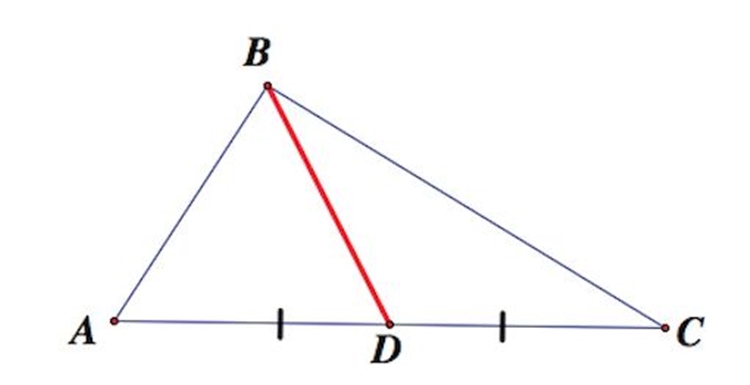
Определение медианы треугольника гласит, что это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В любом треугольнике можно провести ровно 3 медианы.
Чтобы построить медиану конкретного треугольника, нужно:
- Отметить 3 вершины треугольника точками A, B и C
- Найти середину каждой из сторон треугольника
- Соединить точки A, B и C с серединами противоположных сторон
Получившиеся отрезки АМ, BN и CK как раз и будут точка пересечения медиан нашего треугольника ABC.
Чтобы убедиться, что отрезок является медианой треугольника, можно использовать два критерия:
- Отрезок соединяет вершину треугольника и середину противоположной стороны
- Отрезок делится точкой пересечения с другой медианой в отношении 2:1, считая от вершины
Если отрезок удовлетворяет хотя бы одному из этих критериев, то он является медианой.
Где пересекаются медианы и что это за точка
Удивительный факт, но точка пересечения медиан треугольника действительно существует! Более того, все 3 медианы пересекаются в одной-единственной точке, которая называется центр треугольника. Это можно строго математически доказать.
Три медианы треугольника всегда пересекаются в одной точке, которая называется центроид или центр тяжести треугольника.
Эта точка обладает уникальными свойствами. Например, если поместить в центроид треугольника иголку, то фигура будет находиться в равновесии, не прокалываясь!
В центроиде как бы сосредоточен центр тяжести всего треугольника. Это находит применение в физике, технике и других областях.
Кроме того, точка пересечения медиан используется в ряде математических доказательств и вычислений благодаря своим уникальным свойствам.
Как найти координаты точки пересечения медиан
Рассмотрим алгоритм нахождения координат точки пересечения медиан треугольника, если известны координаты его вершин.
- Записать координаты 3 вершин треугольника: A(x1, y1), B(x2, y2) и C(x3, y3)
- Найти координаты середин каждой из сторон
- Записать уравнения 2 медиан в виде уравнений прямых через 2 точки
- Найти точку пересечения этих прямых - это искомая точка пересечения медиан
Рассмотрим конкретный пример для треугольника с вершинами A(1,2), B(3,5), C(4,1).
Определение медианы тетраэдра
Помимо треугольников, определение медианы можно дать и для других многогранников, например тетраэдра.
Медианой тетраэдра называется отрезок, соединяющий вершину тетраэдра с центром противоположной грани. Как и в случае треугольника, медианы тетраэдра тоже пересекаются в одной точке.
Вычисление объема тетраэдра через длину медианы
Одно из применений точки пересечения медиан тетраэдра - это вычисление его объема, если известна длина медианы m:
V = (√2/12)·m3
Эта формула выводится из теорем о подобии тетраэдров и использует свойства медиан.

Применение в физике и технике
Уникальные свойства точки пересечения медиан находят применение не только в математике, но и в смежных областях. Рассмотрим несколько примеров.
Вычисление центра масс системы тел
В физике часто бывает необходимо найти положение центра масс сложной системы тел. Оказывается, это сводится к нахождению точки пересечения медиан некоторого вспомогательного многогранника, построенного определенным образом.
Устойчивость конструкций
При проектировании различных инженерных конструкций важно обеспечить их устойчивость. Смещение центра тяжести конструкции может привести к потере устойчивости и обрушению. Зная расположение точки пересечения медиан, можно это предотвратить.
Создание систем автобалансировки
Некоторые механизмы и роботы используют принцип автобалансировки с помощью смещения центра масс. Управляя точкой пересечения медиан специальной фигуры, можно обеспечивать нужное положение системы в пространстве.
Применение в искусстве и архитектуре
Интересные особенности точки пересечения медиан позволяют использовать ее и в творческих областях.
Композиционный центр в живописи
Художники используют понятие композиционного центра картины - точки, на которую сходятся все линии построения. Часто этот центр выбирается интуитивно. Однако применение математических закономерностей, в частности точки пересечения медиан, позволяет найти оптимальное положение такой точки.
Архитектурные решения на основе медиан
Свойства медиан и их точек пересечения могут использоваться архитекторами и дизайнерами для гармоничного построения сооружений и интерьеров. Например, точка пересечения медиан помещения часто выбирается как оптимальное место для расположения люстры или арт-объекта.
Скульптурные композиции
Существуют занимательные скульптурные группы, демонстрирующие свойства точки пересечения медиан наглядно. Несколько фигур соединены стержнями так, что их общий центр тяжести находится в этой точке, благодаря чему композиция устойчива и сбалансирована.























