Геометрические фигуры хранят множество загадок. Круги и окружности используются повсеместно в науке, технике, искусстве. Давайте разберемся с формулами для вычисления радиусов вписанных и описанных окружностей. Эти знания пригодятся вам на практике.
Базовые понятия окружности
Для начала дадим определения основным терминам.
- Окружность – замкнутая кривая, все точки которой находятся на одинаковом расстоянии от заданной точки (центра).
- Радиус – отрезок, соединяющий центр окружности с любой точкой на ней.
- Диаметр – отрезок, проходящий через центр и соединяющий две точки на окружности.
Окружность обладает полезными свойствами, используемыми во многих областях.
Например, форма колеса соответствует окружности, что позволяет автомобилю ехать плавно. В оптике линзы имеют сферическую форму благодаря свойствам окружности.
Вписанные и описанные окружности
Вписанная окружность – окружность, касающаяся всех сторон некоторого многоугольника. Центр такой окружности лежит внутри этого многоугольника.
Описанная окружность – окружность, все вершины которой лежат на данном многоугольнике. Ее центр располагается снаружи многоугольника.
Знание свойств вписанных и описанных окружностей помогает решать множество геометрических задач. Формулы радиусов таких окружностей часто применяются на практике.
Формулы радиусов вписанной и описанной окружности
Общий вид формул для вычисления радиусов вписанных r и описанных R окружностей:
- S – площадь многоугольника
- P – периметр многоугольника
- a, b, c – стороны многоугольника
Для каждого конкретного вида многоугольника существуют свои формулы радиусов вписанных и описанных окружностей.
Треугольник
| Радиус вписанной окружности | r = S / P |
| Радиус описанной окружности | R = abc / 4S |
Рассмотрим пример вычисления радиуса для треугольника со сторонами 5, 7 и 10 см:
- Находим площадь треугольника по формуле Герона:
S = 14 см2 - Вычисляем периметр:
P = 5 + 7 + 10 = 22 см - Подставляем значения в формулу радиуса вписанной окружности:
r = S / P = 14 / 22 = 1 см
Итак, радиус вписанной окружности равен 1 см.
Правильные многоугольники
Для правильных многоугольников формулы радиусов упрощаются:
- Радиус вписанной окружности:
r = a / (2⋅tan(180°/n)) - Радиус описанной окружности:
R = a / (2⋅sin(180°/n))
Где a – сторона правильного n-угольника.
Например, для правильного шестиугольника (n = 6) со стороной 10 см получим:
- Радиус вписанной окружности:
r = 10 / (2⋅tg(180°/6)) = 10 / √3 = 5цм - Радиус описанной:
R = 10 / (2⋅sin(180°/6)) = 10 / 1 = 5см
Как видим, радиусы совпадают, что верно для всех правильных многоугольников.
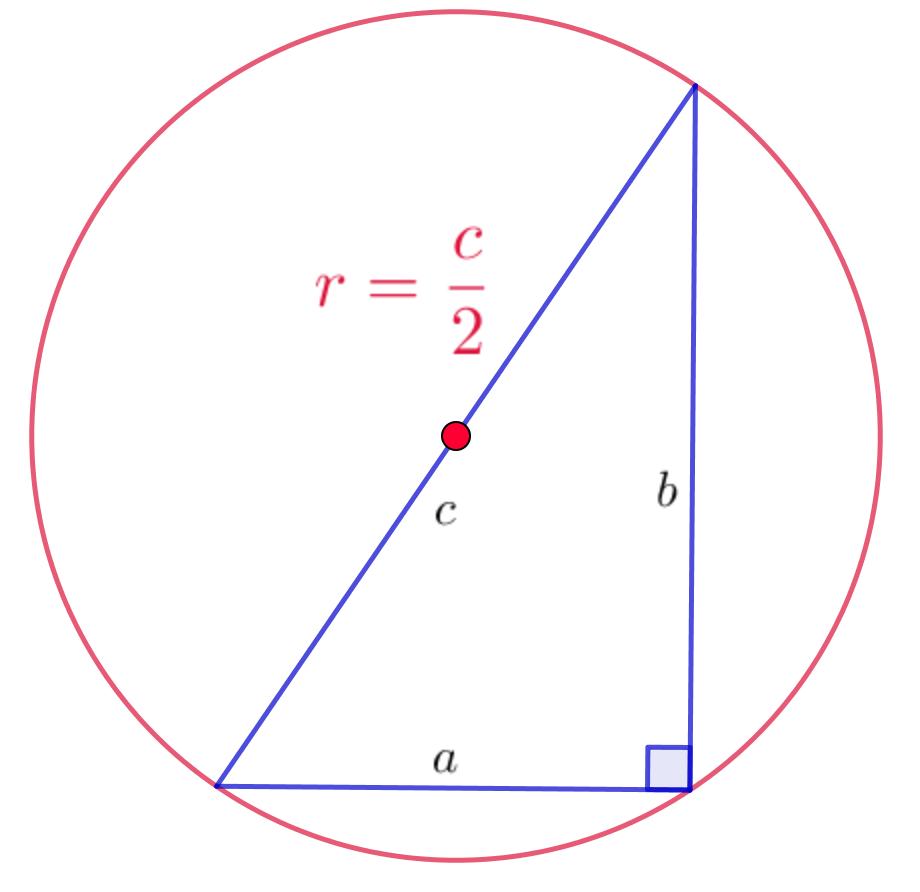
Четырехугольники
Для разных видов четырехугольников также существуют свои формулы радиусов вписанных и описанных окружностей.
Квадрат
- Радиус вписанной окружности:
r = a / √2 - Радиус описанной окружности:
R = a / √2
Где a – сторона квадрата.
Прямоугольник
| Радиус вписанной окружности | r = S / (a + b) |
| Радиус описанной окружности | R = √((a + b)2 + c2) / 4 |
Где a и b – стороны прямоугольника, c – его диагональ.
Параллелограмм
Для параллелограмма формулы радиусов аналогичны формулам для прямоугольника, но с заменой диагонали c на высоту h, опущенную на сторону a.
Ромб
- Радиус вписанной окружности:
r = a / √2 - Радиус описанной окружности:
R = d / 2
Где a – сторона ромба, d – его большая диагональ.
Трапеция
Для трапеции формулы радиусов вписанных и описанных окружностей громоздки, поэтому приводить их здесь не будем. Отметим лишь, что в эти формулы входят стороны, диагонали, углы и высоты трапеции.
Программы для расчета радиусов окружностей

Вычисление радиусов вручную по формулам может быть трудоемким. К счастью, существует множество бесплатных онлайн калькуляторов для расчета радиусов вписанных и описанных окружностей.
Достаточно ввести исходные данные многоугольника, и программа автоматически выдаст значения радиусов.
Применение формул радиусов окружностей
Рассмотрим несколько примеров использования формул радиусов вписанных и описанных окружностей на практике.
Проектирование объектов
При проектировании зданий, сооружений, технических объектов часто приходится иметь дело с окружностями и дугами. Знание соответствующих формул позволяет быстро рассчитать необходимые параметры.
Работа со спутниковыми снимками
Анализируя спутниковые снимки местности, ученые выделяют и исследуют различные объекты, в том числе имеющие форму окружности. Для определения их размеров используют формулы радиусов.
Обработка изображений
При компьютерной обработке изображений часто нужно распознавать круглые объекты, например монеты, колеса машин и так далее. Знание радиусов помогает классифицировать объекты по размерам.
Статистический анализ
Формулы радиусов применяются в статистике при анализе распределений со сферической симметрией. Например, модель нормального распределения использует понятие радиуса.
Кто еще нуждается в знании радиусов окружностей
Кроме перечисленных областей, формулы радиусов вписанных и описанных окружностей применяют в своей работе:
- Геодезисты
- Архитекторы
- Инженеры
- Дизайнеры
- Художники
- Аналитики данных
Поэтому эти знания будут полезны многим специалистам!

























