Деление является одним из основных арифметических действий, с которым мы сталкиваемся еще в начальной школе. Однако не всегда это действие дается нам легко, и в процессе решения примеров на деление могут возникнуть различные ошибки. Давайте разберемся, как правильно выполнять деление чисел, чтобы получать верные результаты.
Прежде всего, давайте определим, что означают такие понятия, как делимое, делитель и частное. Делимое - это число, которое мы делим. Делитель - число, на которое делим. Частное - результат деления. Например, в примере 12 : 3 числа 12 и 3 - это делимое и делитель соответственно, а число 4 - частное.
Как свести деление к вычитанию
Деление чисел можно представить как последовательное вычитание одного числа (делителя) из другого (делимого). Например, чтобы разделить 6 на 2, нужно вычесть 2 из 6, получится 4. Затем еще раз вычесть 2, получится 2. И еще раз вычесть 2, получится 0. Значит, число 2 содержится в числе 6 ровно 3 раза. Таким образом, деление сводится к повторяющемуся вычитанию.
При делении больших чисел процесс вычитания может занять много времени. Поэтому были разработаны специальные алгоритмы, позволяющие свести деление к последовательности более простых операций. Например, деление столбиком, когда делимое записывается над делителем, а результат постепенно подсчитывается снизу вверх. Такой алгоритм экономит время и упрощает вычисления.
Деление в столбик широко применяется при делении натуральных и целых чисел. Для других типов чисел, таких как рациональные, действительные, комплексные, используются более сложные алгоритмы, но в основе их тоже лежит идея последовательного вычитания.
Таким образом, деление чисел всегда можно свести к повторяющемуся вычитанию делителя из делимого с использованием эффективных алгоритмов. Это позволяет проводить деление больших чисел на практике, не прибегая к многократному перебору вариантов.
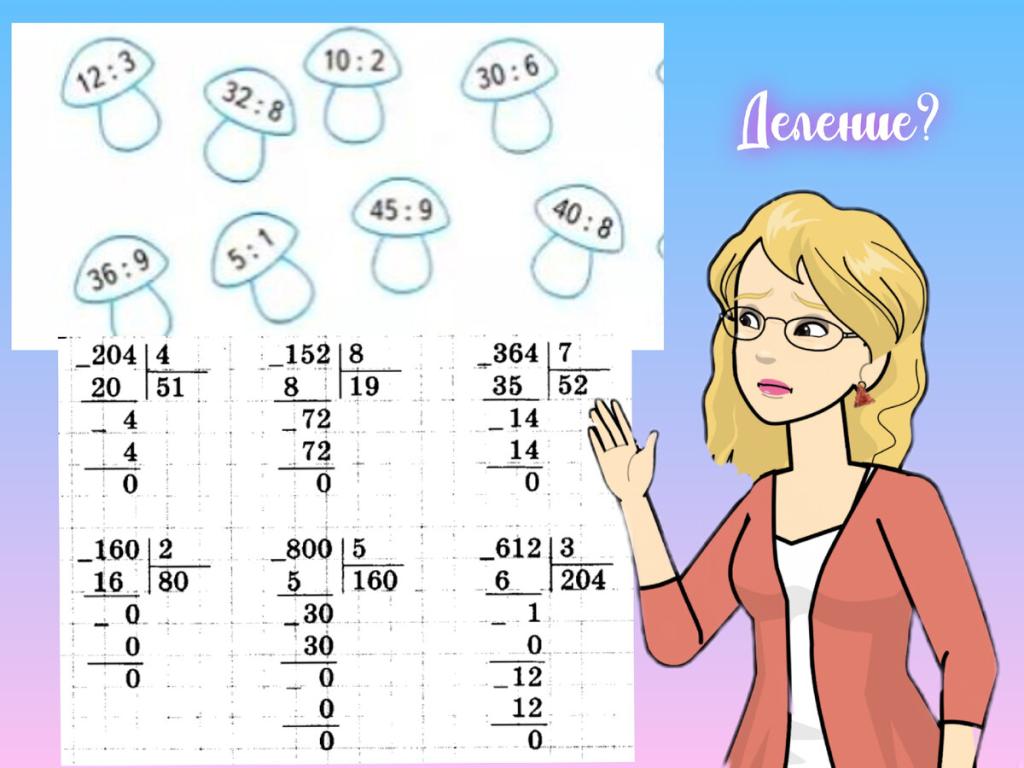
Алгоритмы деления для разных типов чисел
Существуют различные алгоритмы деления чисел в зависимости от их типа.
Для натуральных чисел наиболее распространен алгоритм деления столбиком. При этом делимое записывается над делителем, а результат постепенно подсчитывается снизу вверх. Сначала вычисляется первая цифра частного, затем вторая и т.д. Деление столбиком позволяет эффективно делить большие натуральные числа.
Для деления целых чисел также часто используется алгоритм деления столбиком. Единственное отличие - нужно учитывать знаки чисел при определении знака частного. Кроме того, остаток от деления целых чисел всегда берется по модулю.
Для деления рациональных чисел применяют алгоритмы, основанные на приведении дробей к общему знаменателю. Сначала нужно представить дроби в виде отношения целых чисел. Затем найти наименьший общий знаменатель и привести дроби к нему. После этого деление сводится к делению целых чисел.
Деление действительных чисел, заданных в виде бесконечных десятичных дробей, осуществляется путем постепенного нахождения цифр частного слева направо. Сначала находится цифра перед запятой, затем после запятой и т.д. Этот процесс может длиться бесконечно долго.
Для деления комплексных чисел в алгебраической форме существует формула, позволяющая найти частное двух комплексных чисел через их действительные и мнимые части. При делении в тригонометрической форме делимые модули чисел и вычитаемые аргументы.
Кроме того, разработаны алгоритмы деления матриц, многочленов, векторов и других математических объектов. Во всех случаях основная идея заключается в поиске такой величины, которую можно вычесть из делимого заданное число раз.
Как избежать типичных ошибок при делении
При выполнении деления чисел часто встречаются типичные ошибки. Чтобы их избежать, нужно знать причины и следовать рекомендациям.
Одна из распространенных ошибок - неверное определение порядка действий в примерах со скобками и другими операциями. Чтобы ее не допустить, нужно хорошо знать правила приоритета операций и порядок действий.
Еще одна типичная ошибка - неправильный перенос чисел при делении столбиком. Чтобы ее избежать, следует аккуратно выполнять вычисления и дважды проверять переносимые числа.
При делении рациональных чисел часто забывают приводить дроби к общему знаменателю. Этот этап обязателен, иначе деление будет выполнено неверно.
При делении отрицательных чисел иногда не учитывают нужные знаки частного и остатка. Чтобы этого не произошло, следует хорошо знать правила знаков при делении целых чисел.
Еще одна распространенная ошибка - неверный округление результата деления. Чтобы ее избежать, нужно четко представлять правила округления.
В целом, чтобы не допускать ошибок при делении, рекомендуется: Знать правила приоритета операций Внимательно выполнять вычисления Проверять промежуточные результаты Не пропускать важные этапы Помнить особенности знаков и округления Тщательное следование этим рекомендациям поможет избежать типичных ошибок при выполнении деления.
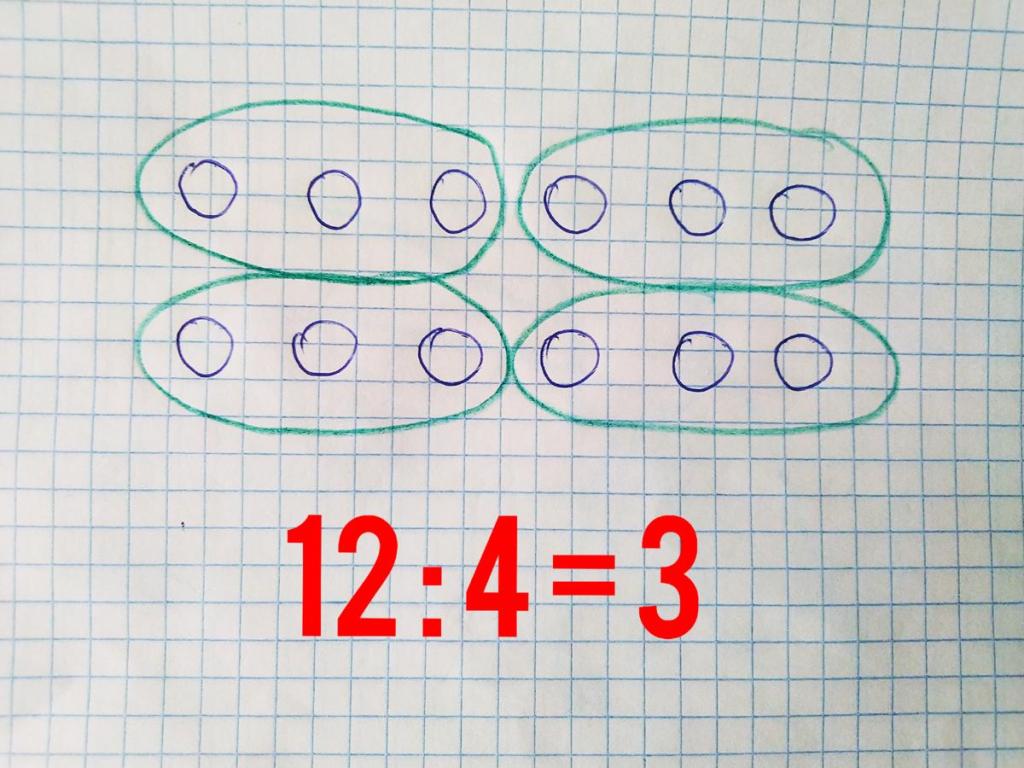
Проверка результата деления
Чтобы убедиться, что деление чисел выполнено верно, можно воспользоваться несколькими способами проверки. Первый способ - использовать обратное действие, то есть перемножить частное на делитель. Если в результате получилось делимое, значит деление выполнено верно. Например, нужно проверить выражение: 12 : 3 = 4. Перемножаем частное 4 и делитель 3. Получаем: 4 · 3 = 12. Так как в результате перемножения получилось делимое 12, значит деление выполнено верно.
- Второй способ проверки - построить схему деления и выполнить деление столбиком. Если полученное в результате деления число совпадает с проверяемым частным, значит деление выполнено верно.
- Третий способ - выполнить деление на калькуляторе и сравнить результаты.
Также можно проверить деление прикидкой. Для этого нужно приблизительно определить, сколько раз делитель умещается в делимом. Например, при делении 45 на 9 делитель уместится примерно 5 раз. Значит, частное должно быть около 5. Этот способ подходит для проверки при решении практических задач.
| Способ проверки | Как проверить |
| Перемножение частного и делителя | Перемножить частное и делитель. Результат должен быть равен делимому. |
| Построение схемы деления | Построить схему и выполнить деление столбиком. Полученное частное должно совпадать. |
| Использование калькулятора | Выполнить деление на калькуляторе. Результаты должны совпадать. |
Регулярно проверяя результаты выполнения деления, можно избежать ошибок и закрепить навык верного деления чисел.
Использование калькулятора при делении
В настоящее время калькуляторы широко используются для выполнения арифметических действий, в том числе деления чисел. Калькулятор позволяет быстро и точно выполнить деление, избегая ошибок в расчетах.
При использовании калькулятора для деления чисел нужно придерживаться определенного порядка действий:
- Ввод делимого числа и нажатие клавиши деления на калькуляторе.
- Ввод делителя и нажатие клавиши равно.
- Получение и запись результата - частного.
При делении на калькуляторе важно правильно расставить скобки, если деление является частью более сложного математического выражения. Скобки позволяют задать нужный порядок действий.
Также следует обращать внимание на количество знаков в делимом и делителе. Если эти числа имеют много знаков, рекомендуется делить по частям, фиксируя промежуточные результаты, чтобы избежать ошибок.
При делении очень больших или очень малых чисел на калькуляторе нужно использовать экспоненциальную форму записи. Это позволит избежать переполнения дисплея и потери точности.
Для проверки результата деления, полученного с помощью калькулятора, можно использовать обратное действие - перемножить частное и делитель. Результат должен совпасть с первоначальным делимым.
При использовании калькулятора для деления в практических задачах рекомендуется:
- Вводить исходные данные в задаче в том же виде, в котором они заданы (например, если в задаче указано 245 метров ткани, вводить именно 245, а не 2.45 и т.д.).
- При необходимости округлять полученный результат деления согласно условию задачи.
- Анализировать, имеет ли смысл полученный результат деления в контексте условия задачи.
Деление чисел в практических задачах
Умение делить числа является важным навыком для решения многих практических задач. Рассмотрим основные рекомендации по применению деления при решении текстовых задач:
- Внимательно прочитать условие задачи, выделяя числовые данные и взаимосвязи между ними.
- Определить, какое действие - деление - позволит найти искомое значение.
- Записать краткое условие задачи с использованием математических символов, включая знак деления.
- Выполнить деление с учетом именованных чисел (например, 180 кг ÷ 30 кг/мешок = 6 мешков).
- Проанализировать, имеет ли смысл полученный результат в контексте задачи.
- Записать ответ на вопрос задачи с указанием единиц измерения, если это необходимо.
Рассмотрим применение деления при решении задачи: В магазине 280 кг моркови разложили в пакеты по 5 кг в каждом. Сколько пакетов получилось?
Решение:
- Дано: в магазине 280 кг моркови.
- Морковь разложили в пакеты по 5 кг в каждом.
- Надо найти: сколько пакетов получилось?
- Выполняем действие: 280 кг ÷ 5 кг/пакет = 56 пакетов
- Ответ: получилось 56 пакетов.
При решении задач с использованием деления полезно оценивать размерность полученного результата. Например, если в ходе решения мы получили скорость 600 км/час, то это явно нереалистичный результат, требующий проверки вычислений.
Другая распространенная задача с делением - нахождение пропорциональной величины. Например, если 1 упаковка печенья стоит 60 рублей, а надо узнать цену 5 упаковок, можно найти: 60 руб. ÷ 1 упак. × 5 упак. = 300 руб.
В задачах на движение также часто используется деление. Например, автобус проехал 360 км за 6 часов. Среднюю скорость можно найти так: 360 км ÷ 6 ч = 60 км/ч.
При решении задач нужно обращать внимание на единицы измерения. Например, нельзя непосредственно делить килограммы на часы или метры на штуки. По ходу решения требуется преобразовать данные к одинаковым единицам.
Таким образом, деление является важным арифметическим действием, позволяющим решать многие практические задачи. Для верного решения нужно четко представлять взаимосвязи между данными, выбирать подходящее действие, анализировать результат с учетом единиц измерения и практического контекста задачи.
Обучение детей делению чисел
Обучение делению чисел является важной частью изучения математики в начальной школе. Деление относится к базовым арифметическим действиям, поэтому его освоение необходимо для дальнейшего изучения математики.
При обучении делению чисел рекомендуется придерживаться следующих основных принципов:
- Научить ребенка сводить деление к вычитанию, показав, что деление - это многократное вычитание одного числа из другого.
- Использовать наглядность - иллюстрации, схемы, практические действия с предметами.
- Начинать с простых примеров на деление в пределах 10, постепенно увеличивая числа.
- Объяснять смысл действия деления - на сколько равных частей разбивается целое.
- Уделять внимание терминологии - делимое, делитель, частное.
- Контролировать понимание зависимости частного от делимого и делителя.
Обучение делению чисел обычно проходит в несколько этапов:
- Подготовительный этап - изучение таблицы умножения, деления с остатком, взаимосвязи умножения и деления.
- Освоение деления на равные части, например, деление фигуры на 2, 4, 8 равных частей.
- Переход к абстрактным числам - деление с большими числами без наглядной опоры.
- Автоматизация навыка деления, закрепление с помощью большого количества примеров и задач.
При обучении делению важно использовать разнообразные didactic материалы: таблицы, схемы, модели деления, дидактические игры. Это помогает ребенку лучше понять суть действия.
Полезно привлекать к обучению делению практические задачи, связанные с повседневной жизнью ребенка. Например, поделить определенное количество конфет поровну между детьми, чтобы понять, сколько конфет получит каждый.
Важно научить ребенка проверять результат деления разными способами: перемножением, выполнением действия в обратном порядке, оценкой разумности ответа. Это поможет избежать ошибок.
После того как ребенок освоит деление абстрактных чисел, полезно перейти к делению величин, имеющих размерность: метры, килограммы и др. Это приблизит деление к реальным задачам.
Таким образом, обучение делению чисел требует постепенности, использования наглядности, разнообразия примеров и задач, а также регулярной проверки понимания ребенком смысла этого арифметического действия.


























