Трапеция является одной из важнейших тем школьного курса геометрии в 8 классе. Знание свойств этого четырехугольника необходимо для решения множества задач ЕГЭ и олимпиад. В данной статье мы подробно разберем, что такое трапеция, какие бывают ее виды и какие формулы используются для вычисления площади.
Будут рассмотрены конкретные примеры задач на нахождение углов, сторон, диагоналей трапеции. Также приведены визуальные иллюстрации для наглядности.
Определение и элементы трапеции
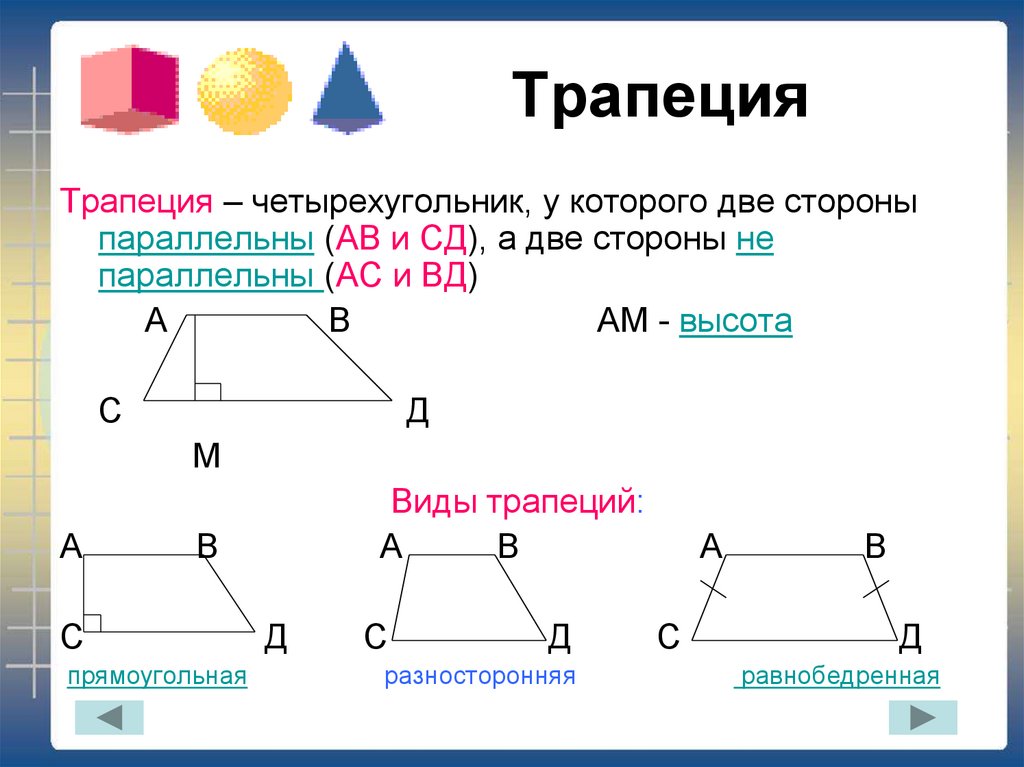
Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие нет. Это один из основных видов четырехугольников, изучаемых в 8 классе. Трапеция имеет следующие основные элементы:
- Основания - две параллельные стороны трапеции обозначаются буквами a и b.
- Боковые стороны - две непараллельные стороны трапеции обозначаются буквами c и d.
- Диагонали - отрезки, соединяющие противоположные вершины трапеции.
Важное свойство трапеции заключается в том, что сумма внутренних углов при одной боковой стороне равна 180° (∠A + ∠B = 180°). Это вытекает из параллельности оснований. Также справедливо равенство ∠C + ∠D = 180°.
Кроме того, у трапеции можно провести среднюю линию - отрезок, соединяющий середины боковых сторон. Эта линия параллельна основаниям и равна полусумме оснований. Например, если основания равны a и b, то средняя линия m = (a + b) / 2.
| Элементы трапеции | Обозначение |
| Основание 1 | a |
| Основание 2 | b |
| Боковая сторона 1 | c |
| Боковая сторона 2 | d |
Таким образом, трапеция - это четырехугольник с двумя параллельными сторонами, обладающий рядом интересных свойств. Знание определения, элементов и формул помогает решать множество задач на вычисление углов, сторон и площадей данного вида четырехугольников.
Свойства и формулы площади
Помимо основных элементов, трапеция обладает множеством интересных свойств, позволяющих вычислять ее углы, стороны и площадь. Рассмотрим некоторые из них подробнее.
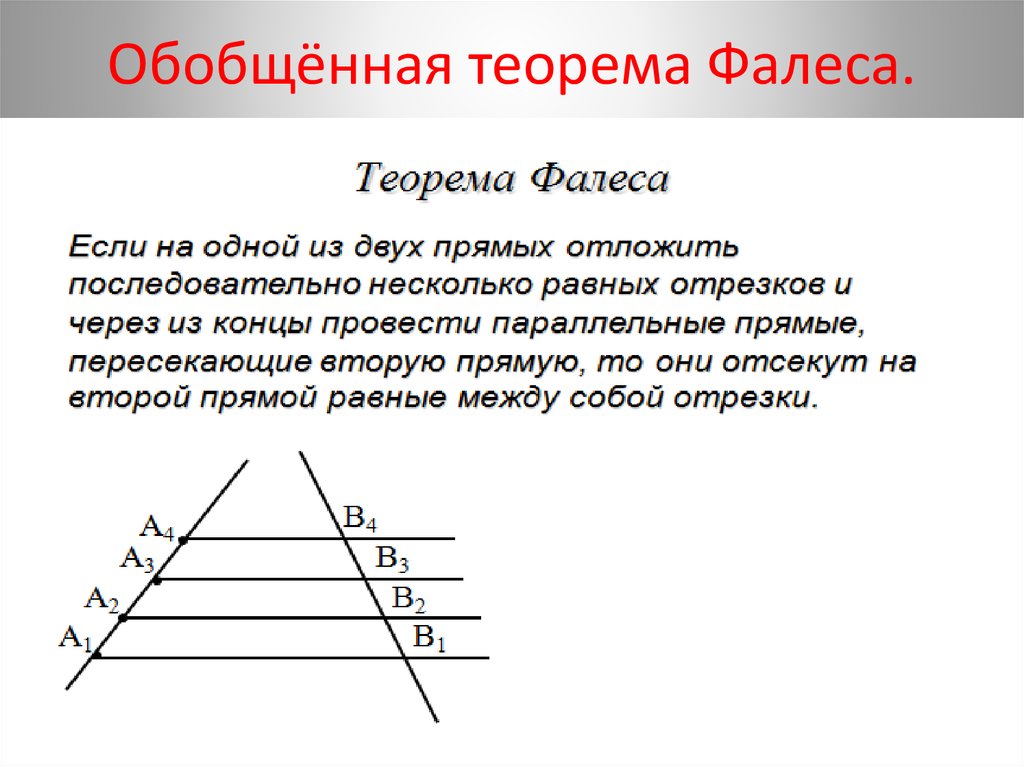
Одно из важнейших свойств трапеции - теорема о средней линии. Она гласит, что средняя линия параллельна основаниям и равна полусумме оснований. Это позволяет по известным основаниям a и b легко найти длину средней линии m = (a + b) / 2. Применение теоремы Фалеса дает еще один результат: отрезки, отсеченные параллельными прямыми на боковых сторонах трапеции, пропорциональны между собой.
Для вычисления углов трапеции используется свойство: сумма углов при одной боковой стороне равна 180°. Это следует из параллельности оснований. Например, если известен один угол ∠A, то ∠B = 180° - ∠A. Аналогично для другой пары углов ∠C и ∠D.
Чтобы найти длину боковой стороны трапеции, применяют теорему о пропорциональных отрезках. Пусть b - известное основание, a c - искомая боковая сторона. Проводим параллельную прямую через точку C. По теореме Фалеса получаем: c / d = B / b, откуда c = (B * b) / d.
Для вычисления площади трапеции используют несколько формул:
- S = ((a + b) / 2) * h, где a и b - основания, h - высота.
- S = m * h, где m - средняя линия, h - высота.
- S = (AC * BD * sinα) / 2, где AC и BD - диагонали, α - угол между ними.
Первая формула является основной для вычисления площади трапеции. Она легко выводится из свойства средней линии. Вторая формула эквивалентна первой и следует из нее подстановкой значения средней линии m. Третья формула получается с помощью теоремы синусов, примененной к треугольнику, образованному диагоналями трапеции и ее боковыми сторонами.
Также существует формула площади трапеции через радиусы вписанной и описанной окружностей: S = (R в - R о) * (a + b) / 2, где R в и R о - радиусы вписанной и описанной окружностей. Она позволяет находить площадь, не зная высоты трапеции.
Кроме того, в задачах на вычисление площади часто используют разбиение трапеции на известные фигуры - треугольники, прямоугольники и др. Это дает возможность применить соответствующие формулы для каждой части.
Примеры типовых задач с трапецией
Рассмотрим несколько примеров типовых задач на применение свойств трапеции из курса геометрии 8 класса. Их решение поможет лучше усвоить формулы и теоремы данной темы.
Пример 1. В трапеции ABCD известно: ∠A = 50°, AB = 8 см, BC = 10 см. Найдите ∠B, ∠C, ∠D и CD.
Решение. По свойству углов трапеции имеем: ∠A + ∠B = 180°.
∠B = 180° - 50° = 130°.
Аналогично, ∠C + ∠D = 180°.
Тогда ∠C = 180° - ∠B = 180° - 130° = 50°.
И ∠D = 180° - ∠A = 180° - 50° = 130°.
Чтобы найти CD, проводим через точку C прямую параллельную AB и применяем теорему Фалеса:
CD / BC = AB / AD
откуда CD = (AB * BC) / AD = (8 * 10) / 8 = 10 (см).
Ответ: ∠B = 130°, ∠C = 50°, ∠D = 130°, CD = 10 см.
Пример 2. В трапеции ABCD известно: ∠A = 105°, ∠B = 45°, AB = 5 дм, AD = 13 дм. Найдите BC, CD и площадь трапеции.
Решение. По свойству углов:
∠C + ∠D = 180°
∠C = 180° - ∠D = 180° - 45° = 135°.
Для нахождения BC применяем теорему Фалеса:
BC / CD = AB / AD
BC = (AB * CD) / AD = (5 * CD) / 13.
Чтобы найти CD, рассмотрим треугольник ABD:
tg45° = CD / AB, откуда CD = AB * tg45° = 5 * 1 = 5 (дм).
Подставляя это значение в формулу, получаем:
BC = (5 * 5) / 13 = 25 / 13 (дм).
Высота трапеции равна:
h = AD * sin105° = 13 * sin105° ≈ 12,2 (дм).
По формуле площади трапеции имеем:
S = ((AB + BC) / 2) * h =
= ((5 + 25/13) / 2) * 12,2 ≈ 94 (дм2).
Ответ: BC = 25/13 дм, CD = 5 дм, S = 94 дм2.
Пример 3. Дана трапеция ABCD с основаниями AB = 28 см и CD = 16 см, диагональю AC = 34 см. Найдите BD, площадь трапеции и ее высоту.
Решение. По теореме Пифагора для треугольника ACD:
BD2 = AC2 + CD2
BD2 = 342 + 162 = 1156
BD = √1156 ≈ 34 см.
Для нахождения площади воспользуемся формулой через диагонали и угол между ними:
S = (AC * BD * sinα) / 2,
где sinα = CD / BD = 16 / 34.
Подставляя значения, получаем:
S = (34 * 34 * 16/34) / 2 = 272 см2.
Высота трапеции равна:
h = 2S / (AB + CD) = 2 * 272 / (28 + 16) = 22 см.
Ответ: BD = 34 см, S = 272 см2, h = 22 см.
Данные примеры показывают, как можно использовать различные свойства и формулы трапеции для нахождения ее элементов и вычисления площади. Решение подобных задач помогает лучше усвоить тему и подготовиться к контрольным работам в 8 классе.
Особые виды: равнобедренная и прямоугольная трапеции
Помимо обычной трапеции, выделяют два ее особых вида, обладающих дополнительными свойствами - равнобедренную и прямоугольную трапеции. Рассмотрим их подробнее.
Равнобедренная трапеция отличается от обычной тем, что ее боковые стороны равны между собой. Это влечет за собой некоторые следствия:
- Углы при основаниях равнобедренной трапеции равны.
- Ее диагонали также равны.
- Средняя линия параллельна основаниям и равна половине каждого из них.
Эти свойства можно доказать с помощью дополнительных построений, используя параллельность сторон трапеции. Они позволяют упростить вычисления углов и сторон в задачах.
Кроме того, для равнобедренной трапеции справедливы признаки: если углы при основании равны или диагонали равны, то боковые стороны тоже равны. Это следует из равенства треугольников, образованных диагоналями и боковыми сторонами.
Формула площади равнобедренной трапеции такая же, как для обычной. Но благодаря равенству боковых сторон высоту всегда можно выразить через стороны или диагонали, что упрощает вычисления.
Прямоугольная трапеция - это трапеция, у которой одна из боковых сторон перпендикулярна основаниям. Это позволяет применить теорему Пифагора и свойства прямоугольных треугольников при решении задач.
У прямоугольной трапеции выполняются соотношения:
- Боковая сторона, лежащая против прямого угла, является высотой трапеции.
- Каждая из диагоналей делит трапецию на два прямоугольных треугольника.
- Диагонали трапеции равны среднему геометрическому ее оснований.
Эти свойства позволяют быстро находить высоту трапеции, определять вид треугольников для использования теоремы Пифагора и выводить формулы диагоналей.
Площадь прямоугольной трапеции равна произведению средней линии на высоту или сумме площадей двух прямоугольных треугольников, на которые она разбивается диагональю.
Рассмотрим несколько примеров задач на равнобедренную и прямоугольную трапеции:
Пример 1. В равнобедренной трапеции ABCD известно: AB = 8 см, AD = 6 см, ∠BAD = 30°. Найдите BC, CD и ∠BCD.
Решение. Поскольку углы BAD и BCD вертикальные, имеем:
∠ABD = 180° - ∠BAD = 180° - 30° = 150°.
Из равенства углов при основании:
∠BCD = ∠ABD = 150°.
По теореме Пифагора для треугольника ABD:
BD2 = AB2 + AD2 = 82 + 62 = 100,
BD = 10 см.
Так как AB = BC и BD = CD, то BC = CD = 10 см.
Ответ: BC = CD = 10 см, ∠BCD = 150°.
Пример 2. В прямоугольной трапеции ABCD известно: ∠A = 90°, AB = 6 см, AD = 10 см, ∠BAD = 45°. Найдите BC, CD и площадь трапеции.
Решение. По теореме Пифагора для треугольника ABD:
BD2 = AB2 + AD2 = 62 + 102 = 136,
BD = 12 см.
BC = BD = 12 см (как катет, лежащий напротив угла 45°).
По теореме Пифагора для треугольника BCD:
CD2 = BC2 + BD2 = 122 + 122 = 288,
CD = 12√2 см.
Высота трапеции равна боковой стороне AB, то есть 6 см.
Площадь: S = (AB + CD) / 2 * h = (6 + 12√2) / 2 * 6 = 54 см2.
Ответ: BC = 12 см, CD = 12√2 см, S = 54 см2.
Таким образом, знание дополнительных свойств равнобедренной и прямоугольной трапеций позволяет упростить решение многих задач в курсе планиметрии 8 класса.


























