Геометрия является одной из древнейших наук, изучающей пространственные отношения и формы. Основы геометрии были заложены еще в трудах древнегреческих математиков, таких как Евклид. С тех пор геометрия значительно развилась и применяется во многих сферах науки и техники.
Как и любая строгая наука, геометрия базируется на определенной системе аксиом - утверждений, которые принимаются за истину без доказательств. Однако очень важно понимать логическую связь между этими аксиомами и выводимыми из них теоремами и следствиями. В данной статье мы разберем основные понятия, связанные с аксиоматическим методом в геометрии.
Что такое аксиома
Аксиома – это положение, принимаемое без доказательств в качестве исходного для построения теории. Аксиомы лежат в основе любой научной теории и не нуждаются в доказательствах в рамках этой теории. Однако важно понимать, что аксиомы – это всего лишь допущения, принимаемые за истинные. Их истинность может быть подтверждена или опровергнута при переходе к более общим теориям.
В геометрии Евклида существует пять основных групп аксиом:
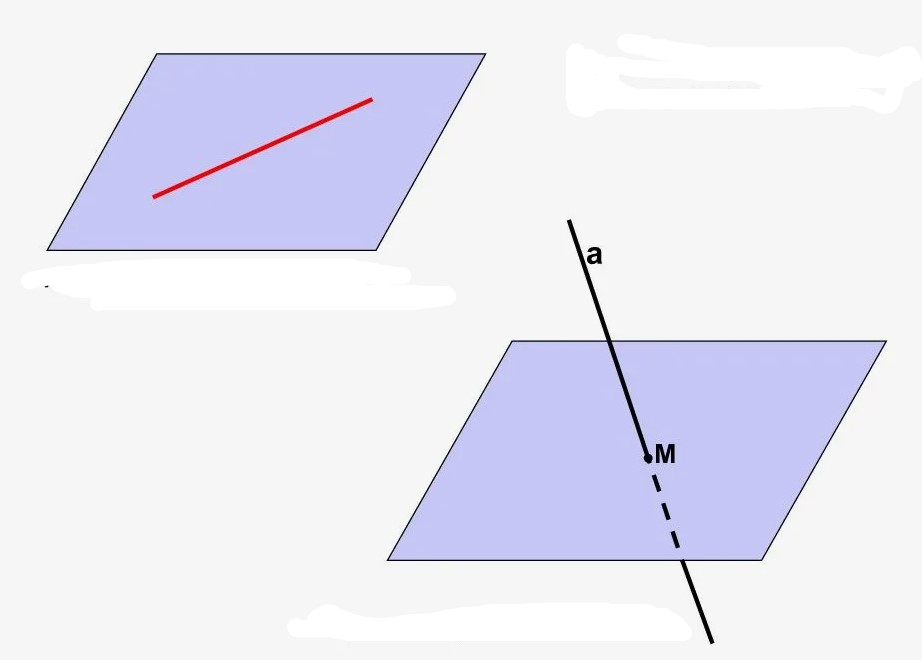
- Аксиомы инцидентности (описывают взаимное расположение точек, прямых и плоскостей).
- Аксиомы порядка (описывают взаимное расположение точек на прямой).
- Аксиомы конгруэнтности (описывают равенство и подобие фигур).
- Аксиомы непрерывности (утверждают, что прямые, плоскости и пространство непрерывны).
- Аксиома параллельности Евклида (через точку, не лежащую на данной прямой, можно провести единственную прямую, параллельную данной).
Эти аксиомы принимаются за истинные, но их истинность не очевидна и требует доказательств при переходе к более общим геометрическим теориям.
Например, в неевклидовых геометриях аксиома параллельности Евклида не выполняется. Лобачевский и Риман в XIX веке построили непротиворечивые геометрические системы, отвергающие евклидову аксиому о параллельных. Таким образом, аксиомы геометрии, хотя и принимаются в ней без доказательства, на самом деле нуждаются в обосновании истинности при интерпретации геометрии как теории реального физического пространства.

Определение и виды теорем
Теорема – это утверждение, логически выводимое из аксиом. В отличие от аксиом, теоремы требуют строгого логического доказательства. Таким образом, если аксиомы задают фундамент геометрии, то теоремы позволяют на этом фундаменте выстраивать все многообразие геометрических фактов.
Различают несколько видов теорем:
- Прямая теорема – стандартное утверждение вида «Если выполнено условие A, то верно утверждение B».
- Обратная теорема – утверждение с переставленными местами условием и заключением по сравнению с прямой теоремой.
- Противоположная теорема – отрицание прямой теоремы.
- Лемма – вспомогательная теорема, используемая при доказательстве более сложных утверждений.
Кроме того, на основе теорем могут быть сформулированы их следствия, которые также подлежат доказательству.
Например, одна из важнейших теорем планиметрии – теорема Пифагора – гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это прямая теорема, позволяющая находить длину неизвестной стороны прямоугольного треугольника, если известны две другие. Из нее выводится множество следствий, например о равенстве расстояний от любой точки до вершин прямоугольника. Теорема Пифагора опирается на "аксиомы геометрии", задающие фундаментальные свойства пространства.
Способы доказательства в геометрии
Доказательство теорем - важнейший элемент геометрии как научной теории. Существует несколько основных способов доказательства геометрических утверждений:
- Прямое доказательство - дедуктивный вывод теоремы из аксиом, ранее доказанных теорем и определений.
- Доказательство от противного - для доказательства исходного утверждения демонстрируется абсурдность или противоречивость его отрицания.
- Доказательство индукцией - путем доказательства справедливости базовых случаев и перехода к общему утверждению для любого значения параметра.
Кроме того, существуют различные методы, облегчающие процесс доказательства:
- Метод замены фигур равными - замена исходной фигуры на равную ей для упрощения доказательства.
- Метод дополнительных построений - введение вспомогательных элементов.
- Переход к противоположному - рассмотрение противоположного утверждения.
Все доказательства в геометрии опираются на ее "аксиомы" - фундаментальные истины, принимаемые без доказательств. Поэтому аксиомы играют ключевую роль в процессе доказательства любой теоремы.
Свойства и признаки геометрических фигур
При изучении геометрических фигур важно различать их свойства и признаки. Свойства - это утверждения, верные для данного класса фигур. Например, у прямоугольника есть свойство - его диагонали равны. Это справедливо для любого прямоугольника.
Признаки же позволяют однозначно определить, что рассматриваемая фигура относится к данному классу. Для прямоугольника таким признаком является равенство его противоположных сторон и прямой угол между ними. Если выполнены оба эти условия - перед нами прямоугольник.
Иногда свойство геометрической фигуры может также выступать и ее признаком. Например, равенство радиусов - и свойство, и признак окружности. Любая окружность имеет это свойство, и если данное свойство выполнено, значит имеем дело с окружностью.
Таким образом, различение свойств и признаков помогает глубже структурировать знания о геометрических фигурах, выявлять их ключевые отличия. А аксиомы геометрии задают фундаментальные свойства пространства, на которых зиждутся все остальные свойства и признаки.
























