Абсцисса - важное понятие в математике, которое используется для определения положения точки на координатной плоскости или в пространстве. Понимание абсциссы необходимо для построения и чтения графиков функций, решения геометрических задач и многого другого.
Давайте разберемся, что означает этот термин и где он применяется.
Определение абсциссы точки
Абсцисса - это координата точки на оси X в прямоугольной системе координат. Абсцисса показывает положение точки относительно начала координат по горизонтали. Абсцисса - термин латинского происхождения, означает «отрезок». В русском языке чаще используют термин координата X.
Для нахождения абсциссы точки А нужно опустить из этой точки перпендикуляр на ось X (ось абсцисс). Точка пересечения перпендикуляра и оси X называется проекцией точки А на ось X и обозначается Ах. Абсцисса точки А равна отрезку ОАх, где О - начало координат. Если точка А лежит правее оси Y, абсцисса положительна. Если левее - отрицательна. Если точка лежит на оси Y, абсцисса равна 0.
Таким образом, зная координаты точки (x, y), мы можем однозначно определить ее положение на плоскости. Абсцисса является одной из двух координат (наряду с ординатой), необходимых для определения положения точки.
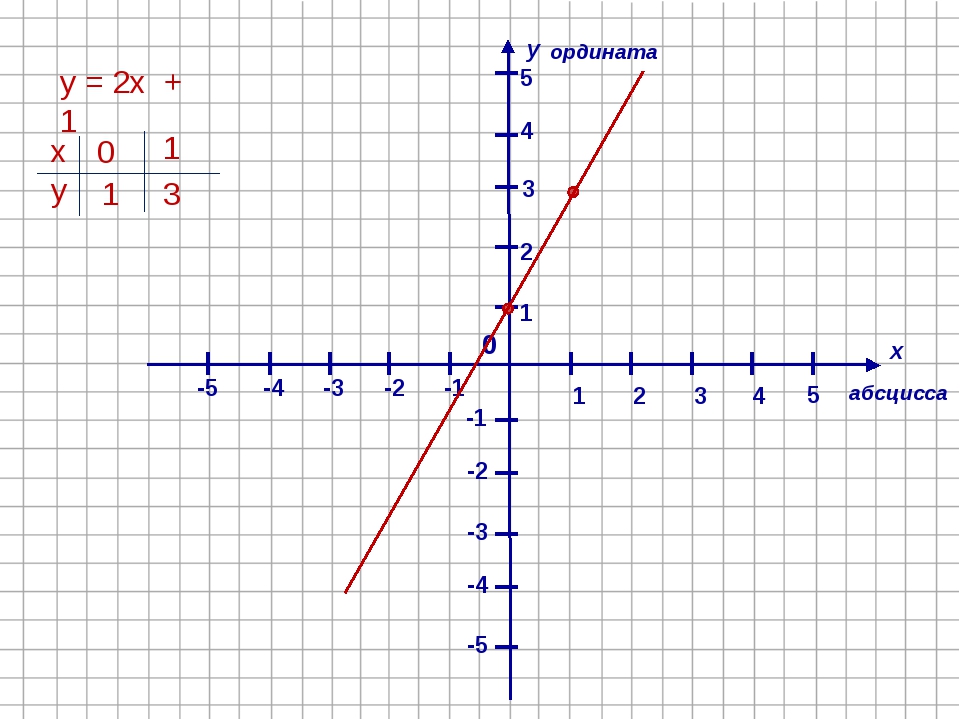
При построении графиков функций абсцисса используется для задания области определения функции. По оси X откладываются значения аргумента, а по оси Y - значения функции. Таким образом, ось X становится осью абсцисс.
Абсцисса в графиках функций
Абсцисса широко применяется при построении графиков функций. В этом случае ось X, то есть ось абсцисс, используется как область определения функции. По оси абсцисс откладываются значения аргумента функции, а по оси ординат - значения самой функции. Таким образом каждой точке на оси абсцисс соответствует определенное функциональное значение на оси ординат.
Рассмотрим несколько примеров использования абсциссы при построении графиков:
- График линейной функции y=kx+b. Здесь k и b - некоторые константы. По оси X откладываются значения аргумента x, а по оси Y - соответствующие значения функции y.
- График квадратичной функции y=ax2+bx+c. Ось абсцисс опять же задает область определения, а по оси ординат откладываются квадратичные значения.
- График тригонометрических функций: синуса, косинуса, тангенса. Абсциссы - углы в радианах, ординаты - значения тригонометрических функций.
Использование абсциссы позволяет наглядно представить функциональную зависимость в виде графика. Анализируя расположение графика относительно осей координат, можно определить свойства функции: возрастание или убывание, экстремумы, нули и т.д.
Применение абсциссы для решения задач
Абсцисса находит применение не только при построении графиков, но и при решении различных геометрических, физических и прикладных задач.
Рассмотрим несколько примеров использования абсциссы:
- Нахождение координат точки на плоскости. Если известны абсцисса и ордината точки, то однозначно можно определить ее положение на координатной плоскости.
- Вычисление расстояния между двумя точками на плоскости. Зная координаты двух точек, по формуле для расстояния между ними можно найти это расстояние.
- Решение уравнений и неравенств. Используя графический метод, уравнение или неравенство можно свести к нахождению точек пересечения графика с осями координат.
- Нахождение характеристик геометрических фигур. Например, можно найти длину отрезка, площадь многоугольника, радиус окружности и т.д., зная координаты соответствующих точек.
- Моделирование физических процессов. Координаты используются для задания начальных условий и последующего анализа модели.
Таким образом, применение абсциссы (то есть координаты точки на оси X) позволяет решать множество задач в геометрии, физике, технике. Это обусловлено тем, что абсцисса вместе с ординатой однозначно задают положение точки на плоскости.
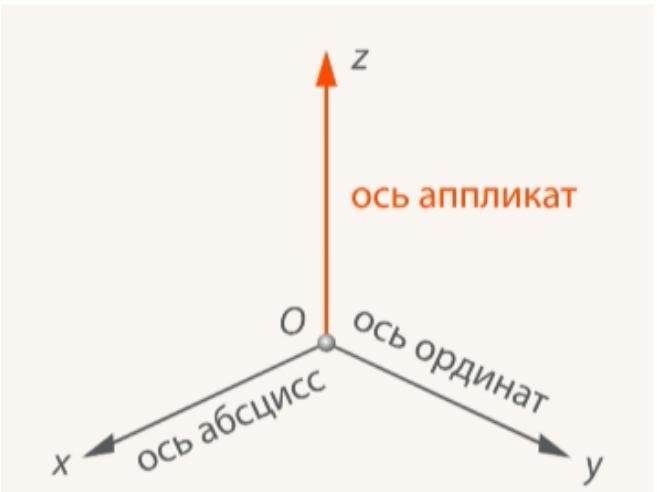
Абсцисса в пространстве
В пространстве для задания положения точки используется прямоугольная система координат, состоящая из трех взаимно перпендикулярных осей: OX, OY и OZ. Ось OX также называют осью абсцисс, OY - осью ординат, а OZ - осью аппликат.
Для того, чтобы однозначно задать положение точки в пространстве, нужно знать ее координаты на всех трех осях - x, y и z. Где x - абсцисса, y - ордината, а z - аппликата. Таким образом, координаты точки M в пространстве записываются в виде (x, y, z).
Абсцисса в пространственной системе координат выполняет ту же роль, что и в двумерном случае - задает положение точки на оси X. Однако для полного определения точки требуется еще дополнительно знать ее координаты на осях Y и Z.
Пространственная система координат широко используется в стереометрии, в частности:
- При описании геометрических тел в пространстве - куба, параллелепипеда, пирамиды, цилиндра, конуса, шара и др.
- Для нахождения координат вершин многогранников и точек на поверхностях тел вращения.
- При вычислении объемов и площадей поверхностей геометрических тел по их координатам.
Кроме геометрических задач, трехмерные декартовы координаты, включающие абсциссу, используются в физике, технике, информатике - везде, где нужно описать положение объекта в пространстве. Например, при моделировании движения тела или распространения тепла.























