Сегодня мы поговорим о предмете под названием информатика. Таблица истинности, разновидности функций, порядок их выполнения – это наши основные вопросы, на которые мы постараемся найти ответы в статье.

Обычно данный курс преподается еще в средней школе, но большое количество учеников является причиной недопонимания некоторых особенностей. А если вы собрались посвятить этому свою жизнь, то просто не обойтись без сдачи единого государственного экзамена по информатике. Таблица истинности, преобразование сложных выражений, решение логических задач – это все может встретиться в билете. Сейчас мы рассмотрим более подробно данную тему и поможем вам набрать больше балов на ЕГЭ.
Предмет логики
Что же это за предмет - информатика? Таблица истинности – как ее строить? Зачем нужна наука логика? На все эти вопросы мы сейчас с вами ответим.
Информатика – это довольно увлекательный предмет. Он не может вызывать затруднения у современного общества, ведь все, что нас окружает, так или иначе, относится к компьютеру.
Основы науки логики даются преподавателями средней школы на уроках информатики. Таблицы истинности, функции, упрощение выражений – все это должны объяснять учителя информатики. Эта наука просто необходима в нашей жизни. Приглядитесь, все подчиняется каким-либо законам. Вы подбросили мяч, он подлетел вверх, но после этого упал опять на землю, это произошло из-за наличия законов физики и силы земного притяжения. Мама варит суп и добавляет соль. Почему когда мы его едим, нам не попадаются крупинки? Все просто, соль растворилась в воде, подчиняясь законам химии.

Теперь обратите внимание на то, как вы разговариваете.
- «Если я отвезу своего кота в ветеринарную клинику, то ему сделают прививку».
- «Сегодня был очень тяжелый день, потому что приходила проверка».
- «Я не хочу идти в университет, потому что сегодня будет коллоквиум» и так далее.
Все, что вы говорите, обязательно подчиняется законам логики. Это относится как к деловой, так и к дружеской беседе. Именно по этой причине необходимо понимать законы логики, чтобы не действовать наугад, а быть уверенным в исходе событий.
Функции
Для того чтобы составить таблицу истинности к предложенной вам задаче, необходимо знать логические функции. Что это такое? Логическая функция имеет некоторые переменные, которые являются утверждениями (истинными или ложными), и само значение функции должно дать нам ответ на вопрос: «Выражение истинно или ложно?».
Все выражения принимают следующие значения:
- Истина или ложь.
- И или Л.
- 1 или 0.
- Плюс или минус.
Здесь отдавайте предпочтение тому способу, который для вас является более удобным. Для того чтобы составить таблицу истинности, нам нужно перечислить все комбинации переменных. Их количество вычисляется по формуле: 2 в степени n. Результат вычисления – это количество возможных комбинаций, переменной n в данной формуле обозначается количество переменных в условии. Если выражение имеет много переменных, то можно воспользоваться калькулятором или сделать для себя небольшую таблицу с возведением двойки в степень.
Всего в логике выделяют семь функций или связей, соединяющих выражения:
- Умножение (конъюнкция).
- Сложение (дизъюнкция).
- Следствие (импликация).
- Эквиваленция.
- Инверсия.
- Штрих Шеффера.
- Стрелка Пирса.
Первая операция, представленная в списке, имеет название «логическое умножение». Ее графически можно отметить в виде перевернутой галочки, знаками & или *. Вторая в нашем списке операция – логическое сложение, графически обозначается в виде галочки, +. Импликацию называют логическим следствием, обозначается в виде стрелки, указывающей от условия на следствие. Эквиваленция обозначается двухсторонней стрелкой, функция имеет истинное значение только в тех случаях, кода оба значения принимают либо значение «1», либо «0». Инверсию называют логическим отрицанием. Штрих Шеффера называют функцией, которая отрицает конъюнкцию, а стрелку Пирса – функцией, отрицающей дизъюнкцию.
Основные двоичные функции
Логическая таблица истинности помогает найти ответ в задаче, но для этого необходимо запомнить таблицы двоичных функций. В этом разделе они будут предоставлены.
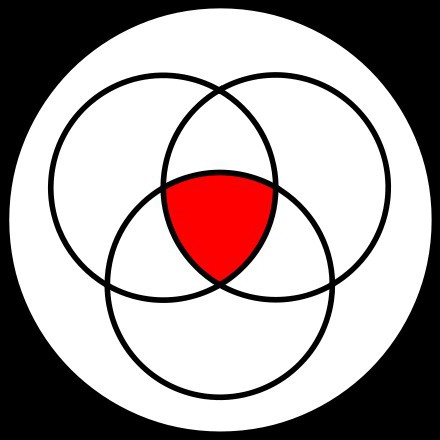
Конъюнкция (умножение). Если два выражения истинны, то в результате мы получаем истину, во всех остальных случаях мы получаем ложь.
+ | + | + |
+ | - | - |
- | + | - |
- | - | - |
Как выглядит таблица, вы узнали, далее нет необходимости приводить ее ко всем формулам. На картинке выше вы можете увидеть, в каких случаях результат равен единице.
Результат – ложь при логическом сложении мы имеем только в случае двух ложных входных данных.
Логическое следствие имеет ложный результат только тогда, когда условие является истиной, а следствие - ложью. Здесь можно привести пример из жизни: «Я хотел купить сахар, но магазин был закрыт», следовательно, сахар так и не куплен.
Эквиваленция является истиной только в случаях одинаковых значений входных данных. То есть при парах: «0;0» или «1;1».

В случае инверсии все элементарно, если на входе есть истинное выражение, то оно преобразуется в ложное, и наоборот. На картинке видно, как она обозначается графически.
Штрих Шиффера будет на выходе иметь ложный результат только при наличии двух истинных выражений.
В случае стрелки Пирса, функция будет истинной только в том случае, если на входе мы имеем только ложные выражения.
В каком порядке выполнять логические операции
Обратите внимание на то, что построение таблиц истинности и упрощение выражений возможно только при правильной очередности выполнения операций. Запомните, в какой последовательности их необходимо проводить, это очень важно для получения верного результата.
- логическое отрицание;
- умножение;
- сложение;
- следствие;
- эквиваленция;
- отрицание умножения (штрих Шеффера);
- отрицание сложения (стрелка Пирса).
Пример №1
Сейчас мы предлагаем рассмотреть пример построения таблицы истинности для 4 переменных. Необходимо узнать в каких случаях F=0 у уравнения: неА+В+С*D
А | В | С | D | неА | С*D | F |
- | - | - | - | + | - | + |
- | - | - | + | + | - | + |
- | - | + | - | + | - | + |
- | - | + | + | + | + | + |
- | + | - | - | + | - | + |
- | + | - | + | + | - | + |
- | + | + | - | + | - | + |
- | + | + | + | + | + | + |
+ | - | - | - | - | - | - |
+ | - | - | + | - | - | - |
+ | - | + | - | - | - | - |
+ | - | + | + | - | + | + |
+ | + | - | - | - | - | + |
+ | + | - | + | - | - | + |
+ | + | + | - | - | - | + |
+ | + | + | + | - | + | + |
Ответом на это задание будет являться перечисление следующих комбинаций: «1;0;0;0», «1;0;0;1» и «1;0;1;0». Как видите, составлять таблицу истинности довольно просто. Еще раз хочется обратить ваше внимание на порядок выполнения действий. В конкретном случае он был следующий:
- Инверсия первого простого выражения.
- Конъюнкция третьего и четвертого выражения.
- Дизъюнкция второго выражения с результатами предыдущих вычислений.
Пример №2

Сейчас мы рассмотрим еще одно задание, которое требует построения таблицы истинности. Информатика (примеры были взяты из школьного курса) может иметь и логические задачи в качестве задания. Коротко рассмотрим одну из них. Виновен ли Ваня в краже мяча, если известно следующее:
- Если Ваня не крал или Петя крал, то Сережа принял участие в краже.
- Если Ваня не виновен, то и Сережа мяч не крал.
Введем обозначения: И – Ваня украл мяч; П – Петя украл; С – Сережа украл.
По данному условию мы можем составить уравнение: F=((неИ+П) импликация С)*(неИ импликация неС). Нам нужны те варианты, где функция принимает истинное значение. Далее необходимо составить таблицу, так как данная функция имеет целых 7 действий, то мы их опустим. Будем вносить только входные данные и результат.
И | П | С | F |
- | - | - | - |
- | - | + | - |
- | + | - | - |
- | + | + | - |
+ | - | - | + |
+ | - | + | + |
+ | + | - | - |
+ | + | + | + |
Обратите внимание на то, что в данной задаче мы вместо знаков «0» и «1» использовали плюс и минус. Это также приемлемо. Нас интересуют комбинации, где F=+. Проанализировав их, мы можем сделать следующий вывод: Ваня участвовал в краже мяча, так как во всех случаях, где F принимает значение +, И имеет положительное значение.
Пример №3

Сейчас предлагаем вам найти количество комбинаций, когда F=1. Уравнение имеет следующий вид: F=неА+В*А+неВ. Составляем таблицу истинности:
А | В | неА | неВ | В*А | F |
Л | Л | И | И | Л | И |
Л | И | И | Л | Л | И |
И | Л | Л | И | Л | И |
И | И | Л | Л | И | И |
Ответ: 4 комбинации.



























