Понятие "сигнал" можно трактовать по-разному. Это код или знак, переданный в пространство, носитель информации, физический процесс. Характер оповещений и их связь с шумом влияют на его дизайн. Спектры сигналов можно классифицировать несколькими способами, но одним из наиболее фундаментальных является их изменение во времени (постоянные и переменные). Вторая основная классификационная категория – частоты. Если рассмотреть виды сигналов во временной области более подробно, среди них можно выделить: статические, квазистатические, периодические, повторяющиеся, переходные, случайные и хаотические. Каждый из этих сигналов обладает определенными свойствами, которые могут влиять на соответствующие проектные решения.

Типы сигналов
Статический по определению является неизменным в течение очень длительного периода времени. Квазистатический определяется уровнем постоянного тока, поэтому его необходимо обрабатывать в схемах усилителя с низким дрейфом. Этот тип сигнала не возникает на радиочастотах, потому что некоторые подобные схемы могут создавать уровень неменяющегося напряжения. Например, непрерывное волновое оповещение с постоянной амплитудой.
Термин «квазистатический» означает «почти неизменный», поэтому относится к сигналу, который необычайно медленно изменяется в течение длительного времени. Он обладает характеристиками, более похожими на статические оповещения (постоянные), чем динамические.
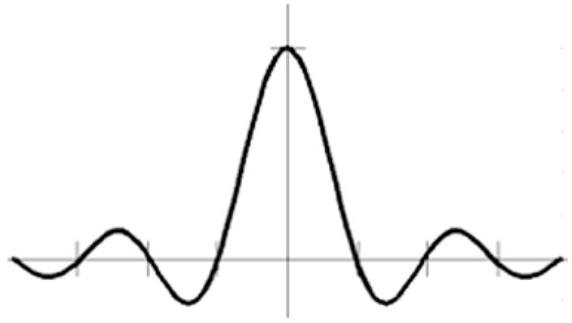
Периодические сигналы
Это те, которые точно повторяются на регулярной основе. Примеры периодических сигналов включают синусоидальные, квадратные, пилообразные, треугольные волны и т. д. Характер периодической формы указывает на то, что она идентична в одинаковых точках вдоль временной линии. Другими словами, если идет продвижение по временной линии ровно на один период (T), то напряжение, полярность и направление изменения формы волны будут повторяться. Для формы напряжения это можно выразить формулой: V (t) = V (t + T).
Повторяющиеся сигналы
Являются квазипериодическими по природе, поэтому имеют некоторое сходство с периодической формой волны. Основное различие между ними обнаруживается путем сравнения сигнала при f (t) и f (t + T), где T – это период оповещения. В отличие от периодического оповещения, в повторяющихся звуках эти точки могут быть не идентичными, хотя они будут очень похожи, так же, как и общая форма волны. Рассматриваемое оповещение может содержать либо временные, либо стабильные признаки, которые варьируются.
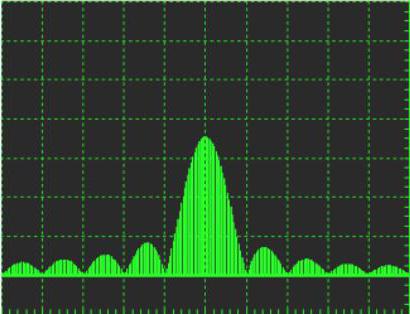
Переходные сигналы и импульсные сигналы
Оба вида являются либо одноразовым событием, либо периодическим, в котором продолжительность очень коротка по сравнению с периодом формы волны. Это означает, что t1 <<< t2. Если бы эти сигналы были переходными процессами, то в радиочастотных схемах намеренно генерировались бы в виде импульсов или переходного режима шума. Таким образом, из вышеизложенной информации можно сделать вывод, что фазовый спектр сигнала обеспечивает колебания во времени, которые могут быть постоянными или периодическими.
Ряды Фурье
Все непрерывные периодические сигналы могут быть представлены основной синусоидальной волной частоты и набором косинусных гармоник, которые суммируются линейно. Эти колебания содержат ряд Фурье формы зыби. Элементарная синусоидальная волна описывается формулой: v = Vm sin(_t), где:
- v – мгновенная амплитуда.
- Vm – пиковая амплитуда.
- "_" – угловая частота.
- t – время в секундах.
Период – это время между повторением идентичных событий или T = 2 _ / _ = 1 / F, где F – частота в циклах.
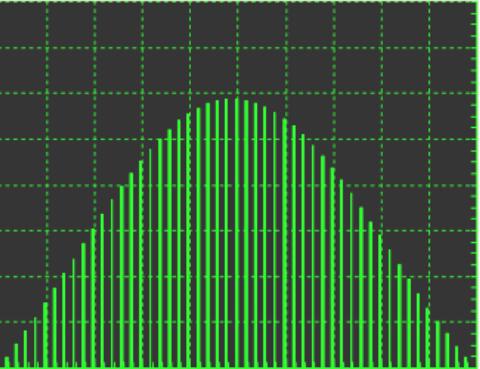
Ряд Фурье, который составляет форму волны, можно найти, если заданная величина разлагается на ее составляющие частоты либо банком частотно–избирательных фильтров, либо алгоритмом цифровой обработки сигналов, называемым быстрым преобразованием. Также может быть использован способ построения с нуля. Ряд Фурье для любой формы волны может быть выражен формулой: f(t) = ao/2+_n–1 [an cos(n_t) + bn sin(n_t). Где:
- an и bn – отклонения компонентов.
- n – целое число (n = 1 является фундаментальным).
Амплитудный и фазовый спектр сигнала
Отклоняющиеся коэффициенты (an и bn) выражаются записью: f(t)cos(n_t) dt. При этом an = 2/T, bn = 2/T, f(t)sin(n_t) dt. Поскольку присутствуют только определенные частоты, фундаментальные плюсовые гармоники, определяемые целым числом n, спектр периодического сигнала называется дискретным.
Термин ao / 2 в выражении ряда Фурье является средним значением f (t) за один полный цикл (один период) формы волны. На практике это компонент постоянного тока. Когда рассматриваемая форма обладает полуволновой симметрией, то есть, максимальный амплитудный спектр сигнала выше нуля, она равна отклонению пика ниже указанного значения в каждой точке по t или (+ Vm = _–Vm_), то нет компонента постоянного тока, поэтому ao = 0.
Симметрия формы волны
Можно вывести некоторые постулаты о спектре сигналов Фурье, исследуя его критерии, показатели и переменные. Из приведенных выше уравнений можно заключить, что гармоники распространяются до бесконечности на всех волновых формах. Ясно, что в практических системах гораздо меньше бесконечных полос пропускания. Поэтому некоторые из этих гармоник будут удалены обычным действием электронных схем. Кроме того, иногда обнаруживается, что более высокие могут быть не очень значительными, поэтому их можно игнорировать. При увеличении n амплитудные коэффициенты an и bn имеют тенденцию к уменьшению. В какой–то момент компоненты так малы, что их вклад в форму волны либо ничтожен для практической цели, либо невозможен. Значение n, при котором это происходит, частично зависит от времени нарастания рассматриваемой величины. Период увеличения определяется, как промежуток, необходимый для того, чтобы волна возрастала с 10% до 90% от ее конечной апмлитудой.
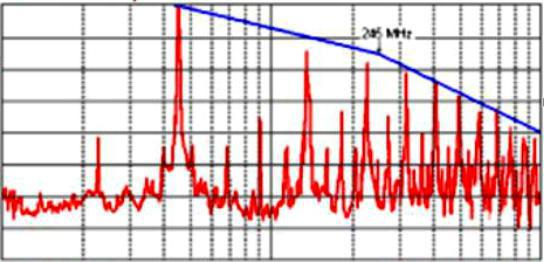
Квадратная волна представляет собой особый случай, поскольку она имеет чрезвычайно быстрое время нарастания. Теоретически она содержит бесконечное количество гармоник, но не все из возможных определяемы. Например, в случае прямоугольной волны найдены только нечетные 3, 5, 7. Согласно некоторым стандартам, точное воспроизведение квадратной зыби требует 100 гармоник. Другие исследователи утверждают, что их необходимо 1000.
Компоненты для ряда Фурье
Другим фактором, определяющим профиль рассматриваемой системы конкретной формы волны, является функция, которая должна быть выявлена, как нечетная или четная. Вторая – это та, в которой f (t) = f (–t), а для первой –f (t) = f (–t). В четной функции присутствуют только косинусные гармоники. Поэтому синусные амплитудные коэффициенты bn равны нулю. Аналогично, в нечетной функции присутствуют только синусоидальные гармоники. Поэтому косинусные амплитудные коэффициенты равны нулю.
Как симметрия, так и противоположные значения могут проявляться несколькими способами в форме волны. Все эти факторы способны влиять на характер рядов Фурье вида зыби. Или, в терминах уравнения, член ao отличен от нуля. Компонент постоянного тока представляет собой случай асимметрии спектра сигнала. Это смещение может серьезно повлиять на измерительные электронные схемы, которые связаны по неменяющемуся напряжению.
Неизменность в отклонениях
Симметрия с нулевой осью возникает, когда на основе точка волны и амплитуда выше нулевой базовой. Линии равны отклонению ниже базовой, или (_ + Vm_ = _ –Vm_). Когда зыбь имеет симметрию с нулевой осью, она обычно не содержит четных гармоник, а присутствуют только нечетные. Такая ситуация встречается, например, в квадратных волнах. Однако симметрия с нулевой осью не встречается только в синусоидальных и прямоугольных зыбях, как показывает пилообразная рассматриваемая величина.
Из общего правила есть исключение. В симметричной форме нулевой оси будут присутствовать. Если четные гармоники синфазные с основной синусоидальной волной. Это условие не будет создавать компонент постоянного тока и не нарушать симметрию нулевой оси. Полуволновая неизменность также подразумевает отсутствие четных гармоник. При этом типе инвариантности форма волны выше нулевой базовой линии и является зеркальным отображением вида зыби.
Сущность других соответствий
Квартальная симметрия существует, когда левая и правая половины сторон осциллограмм являются зеркальными отображениями друг друга на одной стороне оси нуля. Выше оси нуля форма волны похожа на квадратную волну, и действительно, стороны являются идентичными. В этом случае существует полный набор четных гармоник, и любые нечетные, которые присутствуют - это синфазные с основной синусоидальной волной.
Многие импульсные спектры сигналов соответствуют критерию периода. С точки зрения математики, они фактически являются периодическими. Временные оповещения не представлены должным образом рядами Фурье, но могут быть изложены синусоидальными волнами в спектре сигнала. Разница в том, что переходное оповещение является непрерывным, а не дискретным. Общая формула выражена в виде: sin x / x. Она используется также для повторяющихся импульсных оповещений и для переходной формы.
Сэмплированные сигналы
Цифровой компьютер не способен принимать аналоговые входные звуки, а требует оцифрованного представления этого сигнала. Аналого–цифровой преобразователь изменяет входное напряжение (или ток) в репрезентативное двоичное слово. Если устройство работает по часовой стрелке или может запускаться асинхронно, то он будет принимать непрерывную последовательность отсчетов сигнала, в зависимости от времени. При объединении они представляют собой исходный аналоговый сигнал в двоичной форме.
Форма волны в этом случае является непрерывной функцией напряжения времени, V (t). Сигнал отбирается другим сигналом p (t) с частотой Fs и периодом выборки T = 1 / Fs, а затем позже реконструируется. Хотя это может быть достаточно репрезентативным для формы волны, она будет реконструирована с большей точностью, если частота дискретизации (Fs) увеличится.
Бывает, что синусоидальная волна V (t) отбирается импульсным оповещением дискретизации p (t), который состоит из последовательности одинаково расположенных узких величин, разнесенных во времени T. Тогда частота спектра сигнала Fs равна 1 / T. Полученный результат является еще одним импульсным ответом, где амплитуды представляют собой выборочную версию исходного синусоидального оповещения.
Частота дискретизации Fs по теореме Найквиста должна в два раза превышать максимальную частоту (Fm) в спектре Фурье применяемого аналогового сигнала V (t). Чтобы восстановить исходный сигнал после отбора проб, необходимо пройти выборочную форму волны через фильтр низких частот, который ограничивает полосу пропускания до Fs. В практических радиочастотных системах многие инженеры определяют, что минимальная скорость Найквиста недостаточна для хороших репродукций выборочной формы, поэтому нужно указывать увеличенную быстроту. Кроме того, некоторые методы передискретизации используются для резкого снижения уровня шума.
Анализатор спектра сигнала
Процесс выборки аналогичен форме амплитудной модуляции, в которой V (t) является построенным оповещением со спектром от постоянного тока до Fm, а p (t) - несущей частотой. Полученный результат напоминает двойную боковую полосу с несущей величиной АМ. Спектры сигналов модуляции появляется вокруг частоты Fo. Фактическая величина немного сложнее. Подобно нефильтрованному радиопередатчику AM, она появляется не только вокруг основной частоты (Fs) несущей, но также и на гармониках, расположенных с интервалами Fs вверх и вниз.
При условии, что частота дискретизации соответствует уравнению Fs ≥ 2Fm, исходный отклик восстанавливается из выборочной версии, передавая его через фильтр нижних колебаний с меняющейся отсечкой Fc. При этом возможно передавать только спектр аналогового звука.
В случае неравенства Fs <2Fm возникает проблема. Это означает, что спектр частотного сигнала похож на предыдущий. Но разделы вокруг каждой гармоники перекрываются так, что "–Fm" для одной системы меньше "+Fm" для следующей более низкой области колебаний. Это перекрытие приводит к дискретизированному сигналу, ширина спектра которого восстанавливается фильтрацией нижних частот. Он будет генерировать не исходную частоту синусоидальной волны Fo, а более низкую, равную (Fs – Fo), и информация, переносимая в форме волны, теряется или искажается.


























