В математике логарифм является функцией, обратной экспоненциальной. Это означает, что логарифм lg - это степень, в которую нужно возвести число b, чтобы в результате получить x. В простейшем случае он учитывает повторное умножение одного и того же значения.
Рассмотрим конкретный пример:
1000 = 10 × 10 × 10 = 103
В данном случае это - логарифм lg по основанию десять. Равен он трем.
lg101000 = 3
В общем случае выражение будет выглядеть так:
lgbx = a
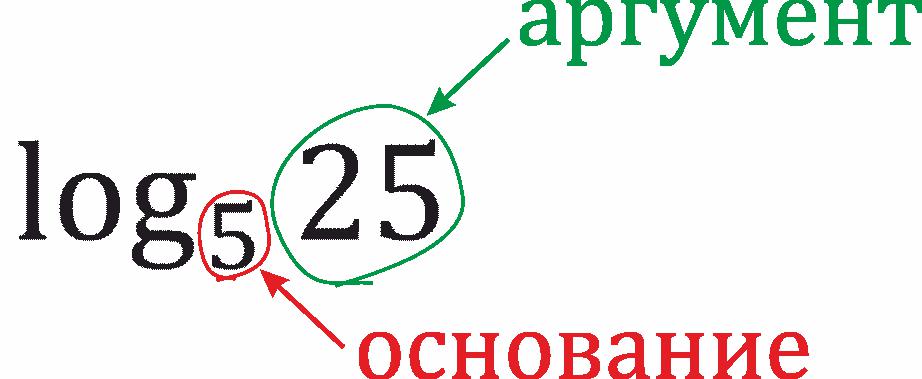
Возведение в степень позволяет любому положительному действительному числу быть увеличенным до любой реальной величины. Результат при этом всегда будет большим, чем ноль. Поэтому логарифм для любых двух положительных действительных чисел b и x, где b не равен 1, всегда является уникальным вещественным числом a. Более того, оно определяет соотношение между возведением в степень и логарифмом:
lgbx = a, если ba = x.
История
История логарифма (lg) берет начало в Европе семнадцатого века. Это открытие новой функции расширило сферу анализа за пределы алгебраических методов. Метод логарифмов был публично предложен Джоном Нейпиром в 1614 году в книге под названием Mirifici Logarithmorum Canonis Descriptio ("Описание замечательных правил логарифмов"). До изобретения ученого существовали другие методы в сходных областях такие, как использование таблиц прогрессий, разработанных Йостом Бюргги приблизительно в 1600 году.

Десятичный логарифм lg - это логарифм с основанием, которое равно десяти. Впервые действительные логарифмы использовались с эвристическими методами для преобразования операции умножения в сложение, что облегчало быстрое вычисление. Некоторые из этих методов использовали таблицы, полученные из тригонометрических тождеств.
Открытие функции, которая теперь известна как логарифм (lg), связывают с попыткой сделать квадратуру прямоугольной гиперболы Грегори де Сент-Винсентом, бельгийцем, проживающем в Праге.
Использование
Логарифмы часто используются и вне математики. Некоторые из этих случаев связаны с понятием масштабной инвариантности. Например, каждая камера оболочки наутилуса является приблизительной копией следующей, уменьшенной или увеличенной в определенное количество раз. Это называют логарифмической спиралью.

Размеры автомодельных геометрических форм, части которых внешне похожи на окончательное изделие, также основаны на логарифмах. Логарифмические шкалы полезны для количественной оценки относительного изменения значения. Более того, поскольку функция logbx растет очень медленно при больших х, для сжатия крупномасштабных научных данных используются логарифмические шкалы. Логарифмы также встречаются в многочисленных научных формулах таких, как уравнение Фенске или уравнение Нернста.
Вычисление
Некоторые логарифмы можно легко вычислить, например log101000 = 3. В общем случае они могут вычисляться с использованием степенных рядов или среднего арифметично-геометрического значения или извлекаться из предварительно рассчитанной таблицы логарифмов, которая обладает высокой точностью.
Итеративный метод для решения уравнений, придуманный Ньютоном, также может быть использован для нахождения значения логарифма. Так как обратной функцией для логарифмической является экспоненциальная, то процесс вычисления сильно упрощается.
























