Не зря считается, что математика - царица наук, ведь она является самой точной из всех ныне существующих. Это фундаментальная наука, способствующая нахождению и объяснению общих законов природы. Одним из разделов математики является тригонометрия.
Общие сведения о тригонометрии
Тригонометрия – область математических знаний, специализирующаяся на изучении тригонометрических функций, которые применяются в геометрии.
История возникновения тригонометрических функций связана с определенным этапом развития науки и человеческими достижениями. Тригонометрия возникла в то время, когда в мире уже существовало зодчество, наука, ремесла. Зачатки тригонометрии замаячили на горизонте научных знаний в тот момент, когда люди стали усиленно изучать прямоугольные треугольники и прослеживать закономерную взаимосвязь между длинами сторон при острых углах и самими острыми углами.
Если обратиться к истории, то можно сказать, что именно древнегреческие математики, задавшись целью измерить длину круга, сообразили, что это можно сделать, предварительно измерив длину дуги (25 % всей длины круга), именно при помощью техники хорд.
Первые тригонометрические таблицы были созданы древнегреческим математиком Гиппархом Никейским, который первым в истории человечества свел в таблицы величины дуг и хорд для набора различных углов.
Тригонометрические знания сегодня используются практически во всех науках и отраслях точных знаний, что является феноменальным фактом. Эти знания достаточно активно применяются в физике, геометрии, инженерии, а также в астрономии, географии, музыке, финансовом анализе, электронике, статистике, теории вероятности, медицине, фармацевтике, архитектуре и компьютерной графике.
Тригонометрические функции
Набор тригонометрических функций может быть представлен такой классификацией:
- Прямые функции - синус (sin x); косинус (cos x).
- Производные функции - тангенс (tg x); котангенс (ctg x).
- Другие функции - секанс (sec x); косеканс (cosec x).
Данные функции взаимосвязаны. Их практическое применение регламентируется несколькими основными формулами, остальные вычислительные процессы совершаются путем нахождения производных этих формул.
Основные формулы тригонометрии
Синус и косинус являются функциями, которые наглядно изображаются в виде кривых в известной еще со школьной скамьи декартовой системе координат (другое название этой системы – ХУ-площадь). Основными свойствами кривых являются периодичность, бесконечная дифференциация, непрерывность.
Что же делать, если срочно нужно вспомнить 10 класс и основные формулы тригонометрии? А учебников по алгебре и геометрии рядом нет... В этом вам поможет таблица, в которой приведены основные формулы тригонометрии.
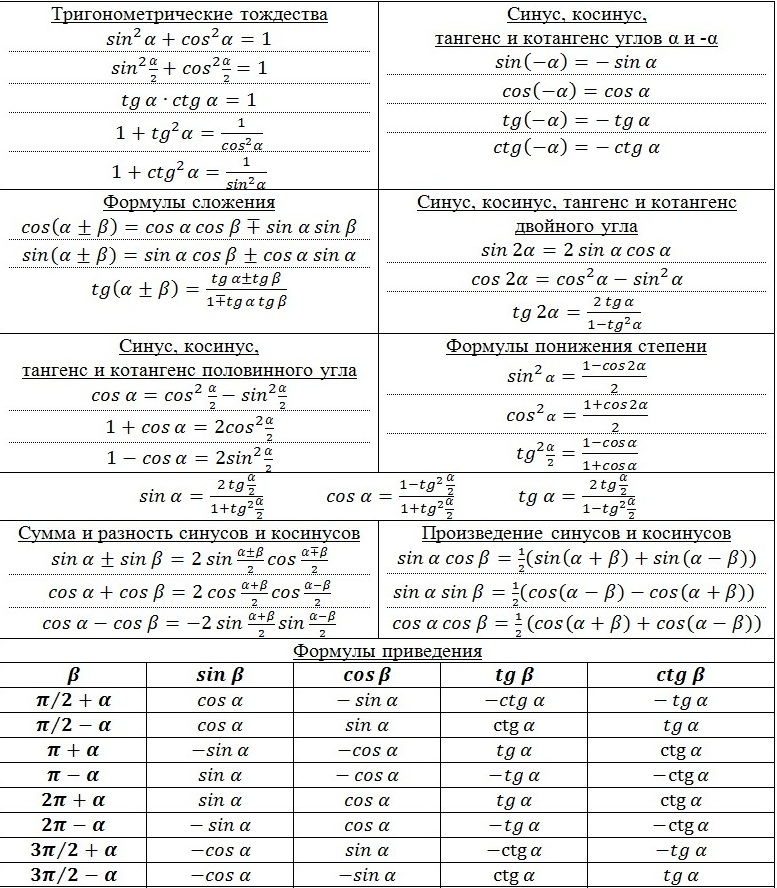
Данная таблица является хорошим вспомогательным средством для того чтобы вспомнить то, что изучалось еще в старшей школе. Таблица "Основные формулы тригонометрии" кажется весьма сложной, ведь информации здесь представлено очень много, кажется, что ее невозможно запомнить. Но это только на первый взгляд. Ведь основных формул всего несколько, они достаточно просты, а от них можно отталкиваться и решать более тяжелые тригонометрические задачи. Эти основные формулы предполагают простые вычислительные действия, такие как сложение, деление, умножение и вычитание.
Что может дать тригонометрия человеку?
Сегодня тригонометрия является частью специфического гармонического анализа в математике, который тщательно изучают и пытаются совершенствовать регулярно великие умы современности. В основе тригонометрии заложены специфические функции математического аппарата, который напрямую связан с исследованием колебательных движений и регулярно повторяющихся процессов. Это, например, периодические колебания, волны и даже некоторые атмосферные процессы.

























