Тригонометрия является важной частью математики, знания которой широко используются в астрономии и при ориентировании на местности. В данной статье рассматривается определение синуса, косинуса, тангенса и котангенса как основных тригонометрических функций.
Что такое тригонометрия?
Это наука, которая изучает количественные свойства треугольников, о чем говорит ее название. Процесс изучения этих простых плоских фигур осуществляется с использованием так называемых тригонометрических функций.
Еще в древнем Вавилоне и Египте люди сталкивались с задачами, требующими знания соотношения между сторонами и углами треугольника (например, при строительстве египетских пирамид). Однако до нашего времени не дошли точные свидетельства того, что вавилоняне и египтяне располагали необходимой математической теорией для решения задач подобного рода.

Развитие тригонометрия получила на заре нашей эры, благодаря достижениям древнегреческих ученых. Первые таблицы тригонометрических функций были составлены лишь во второй половине XV века.
Прямоугольный треугольник
Перед тем как давать определение синусу и другим тригонометрическим функциям, необходимо пояснить, что представляет собой прямоугольный треугольник. У него один из углов равен 90o.
Зная, что сумма углов в этой фигуре равна 180o, можно с уверенностью сказать, что два других угла в сумме составят 90o. При этом каждый из них будет меньше, чем прямой угол.
Стороны прямоугольного треугольника имеют названия. Отрезок, лежащий против прямого угла, называется гипотенузой. Две другие стороны - это катеты.
Введение тригонометрических функций
Теперь можно дать определение синусу и косинусу угла, а также тангенсу и котангенсу. Для этого построим окружность единичного радиуса. Ниже на рисунке представлен треугольник ABC, у которого отрезок AB = 1 - является гипотенузой (радиус окружности), AC и CB - катеты.
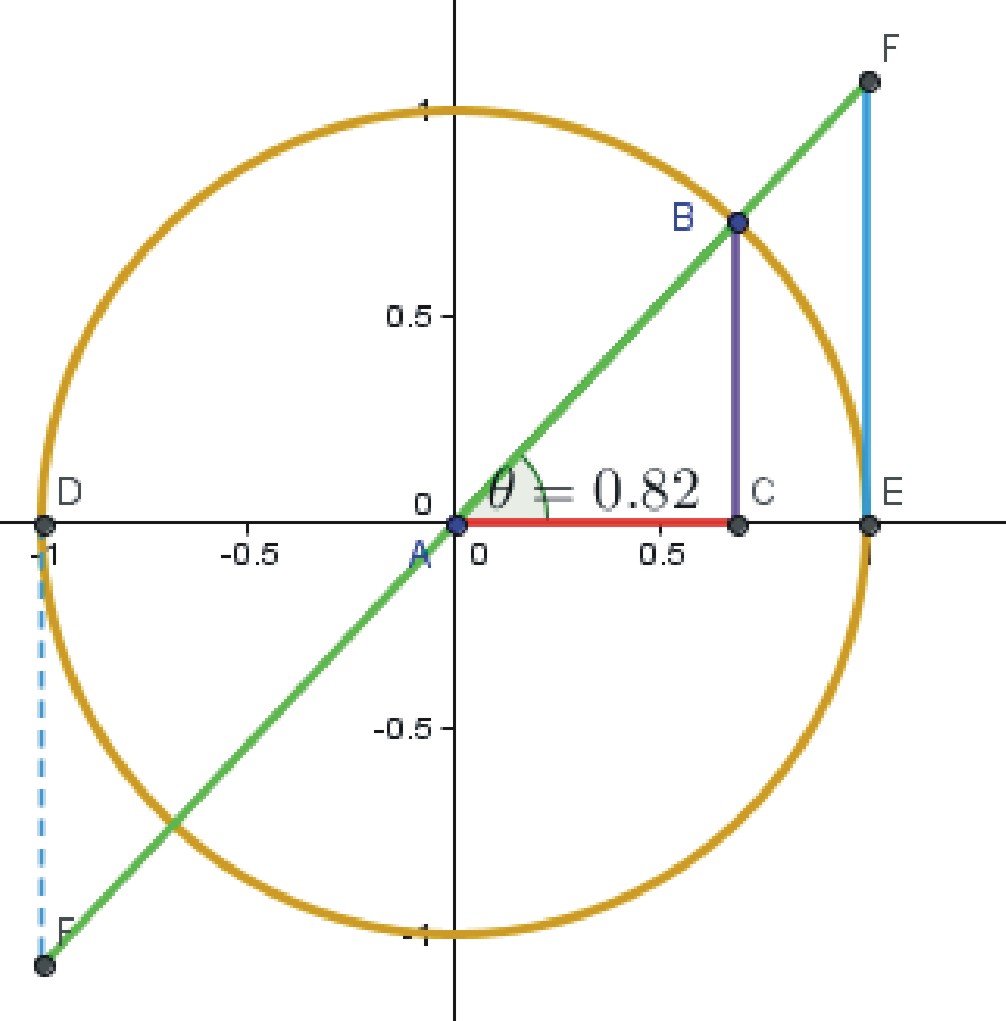
Давая определение синуса угла, следует сказать, что он равен отношению отрезка BC к отрезку AB. Записывается это следующим образом: sin(θ) = BC/AB. Поскольку AB = 1, то sin(θ) = BC. Иными словами, под синусом угла прямоугольного треугольника понимают отношение катета, лежащего напротив этого угла, к гипотенузе.
Теперь определение косинуса угла. Это отношение катета, прилежащего к рассматриваемому углу, к гипотенузе. Для рисунка выше имеем: cos(θ) = AC/AB = AC.
Тангенс угла - это тригонометрическая функция, которая определяется отношением катета, противолежащего к данному углу, к прилежащему катету. То есть tg(θ) = BC/AC.
Наконец, котангенс угла - это отношение прилежащего катета к противолежащему, то есть ctg(θ) = AC/BC.
Свойства синуса и других тригонометрических функций
Из введенных определений синуса, косинуса угла и других функций следуют несколько важных выводов об их свойствах:
- Во-первых, тригонометрические функции являются безразмерными величинами.
- Во-вторых, их значение не зависит от размеров треугольника. Последний факт легко доказать, если обратиться к тому же рисунку вверху и рассмотреть треугольники ABC и AFE. Эти треугольники являются подобными, так как имеют общий угол в вершине A, это означает, что выполняется следующее равенство: BC/AB = FE/AF = sin(θ). Аналогичные равенства можно привести для остальных тригонометрических функций.
- В-третьих, любая тригонометрическая функция может быть выражена с использованием максимум двух других. Это утверждение верно, поскольку все три стороны треугольника фигурируют в выражениях для двух тригонометрических функций. Например, tg(θ) = sin(θ)/cos(θ).
Периодичность функций
Это свойство специально было вынесено в отдельный пункт статьи, поскольку его рассмотрение заслуживает отдельного внимания.
Если вращать отрезок AB (см. рис. выше) против часовой стрелки, то точка B пробежит всю окружность единичного радиуса. Как при этом будут меняться тригонометрические функции?
Рассмотрим синус. Согласно определению синуса угла, когда θ = 0, то BC = 0, то есть sin(0o) = 0. По мере возрастания угла θ, увеличивается длина отрезка BC. При этом длина AB остается неизменной. Это означает, что sin(θ) постоянно увеличивается. Когда угол θ = 90o, то BC=AB и sin(90o) = 1.
Дальнейшее вращение AB против часовой стрелки приводит к уменьшению значения синуса до нуля при угле 180o (sin(180o)=0).
Для углов со значениями лежащими между 180o и 270o синус снова увеличивается по модулю, но уменьшается в абсолютных значениях, поскольку отрезок BC будет лежать в отрицательной области оси ординат. В итоге sin(270o) = -1.
Наконец, в 4-м квадранте окружности, когда угол меняется от 270o до 360o, абсолютное значение синуса увеличивается, но модуль его уменьшается до тех пор, пока при 360o он снова не станет равным нулю (sin(360o) = sin(0o) = 0).
Из проведенного анализа следует, что синус является периодической функцией, которая повторяет свои значения каждые 360o. В тригонометрии обычно пользуются не градусами, а радианами. Напомним, что 2*pi радиан равно 360o, где pi = 3,14 - число пи. График функции sin(x) приведен на главном фото статьи.
Если провести аналогичные рассуждения, то можно показать, что косинус - это периодическая функция с таким же периодом, как и для синуса, то есть T = 2pi. Тангенс и котангенс тоже являются периодическими, только для них T =pi.
Таблица значений тригонометрических функций
Эта таблица включает в себя данные о значениях синуса, косинуса, тангенса и котангенса для набора углов. Школьников заставляют учить эти значения наизусть.
В настоящее время, благодаря развитию информатики, все языки программирования и калькуляторы снабжены соответствующими библиотеками, которые позволяют быстро рассчитать значения любой тригонометрической функции за доли секунды.
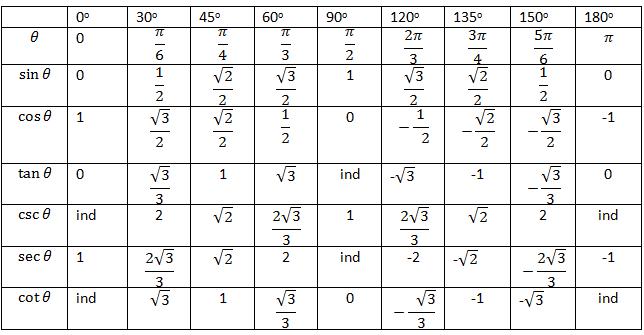
Ниже приводится таблица, в которой приведены значения для всех названных функций набора углов. Которые представлены, как в градусах, так и в радианах. Буквы "ind" означают, что функция для этого угла имеет неопределенное значение. Помимо основных четырех тригонометрических функций, в таблице также приводятся секанс (sec) и косеканс (csc), которые представляют собой обратные косинус и синус, соответственно.
Теорема Пифагора и связь синуса и косинуса
Поскольку определение синуса и косинуса угла основано на использовании прямоугольного треугольника, то эти функции можно связать, если воспользоваться теоремой Пифагора.
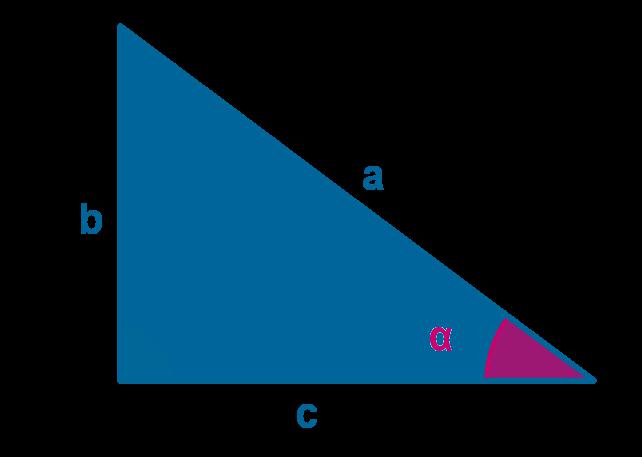
Для изображенного выше прямоугольного треугольника имеем: sin(α) = b/a и cos(α) = c/a. Теорема Пифагора записывается так: c2 + b2 = a2. Если левую и правую части этого выражения поделить на a2, а затем подставить формулы для синуса и косинуса, то получим: (sin(α))2 + (cos(α))2 = 1.


























