Римская нумерация возникла, как следует из названия, в Древнем Риме. Существует семь основных символов: I, V, X, L, C, D и M. Впервые эти символы начали использовать между 900 и 800 годами до н. э.
Цифры были разработаны для использования в качестве общего метода подсчета, необходимого для развития отношений и торговли. Подсчет пальцев выходил из-под контроля, так сказать, когда при счете доходили до 10.
Значение римских цифр
Считается, что система подсчета была разработана на основе руки человека.
Одна линия, или I, символизирует одну штуку чего-либо, или, соответственно, один палец. V представлял собой пять пальцев, в частности V-образную форму, сделанную большим и указательным пальцами. X соответствовал двум рукам (соединенные в одной точке, они образуют две V).
Однако точное происхождение этих цифр римской нумерации неясно. При этом изменения в их формах с III века до нашей эры хорошо известны. Представленное выше происхождение римских цифр основано на теории истории римской нумерации немецкого ученого Теодора Моммсена (1850), получившей широкое признание. Однако изучение надписей, оставленных этрусками, которые правили Италией до латинян, показывает, что римляне приняли этрусскую численную систему, начиная с V века до нашей эры. Но есть и явное различие: этруски читали свои числа справа налево, а римляне читали их слева направо.

Римская нумерация: числа с большим значением, полученные из других символов
M = 1000. Первоначально это значение представляла греческая буква phi – Φ. Иногда оно представлялось как C, I и обратная C: CIƆ, что отдаленно похоже на М. Исследователи считают совпадением, что латинское слово mille используется для обозначения тысячи.
D = 500. Символом для этого числа первоначально был знак IƆ – половина тысячи (CIƆ).
C = 100. Первоначальным символом этого числа, вероятно, был тета (Θ), а позже стала буква C.
L = 50. Первоначально значение этого символа рассматривалось как наложенные V и I или буква psi – Ψ, сглаженная таким образом, чтобы выглядеть, как инвертированная T. Затем, в конце концов, она стала похожа на L.
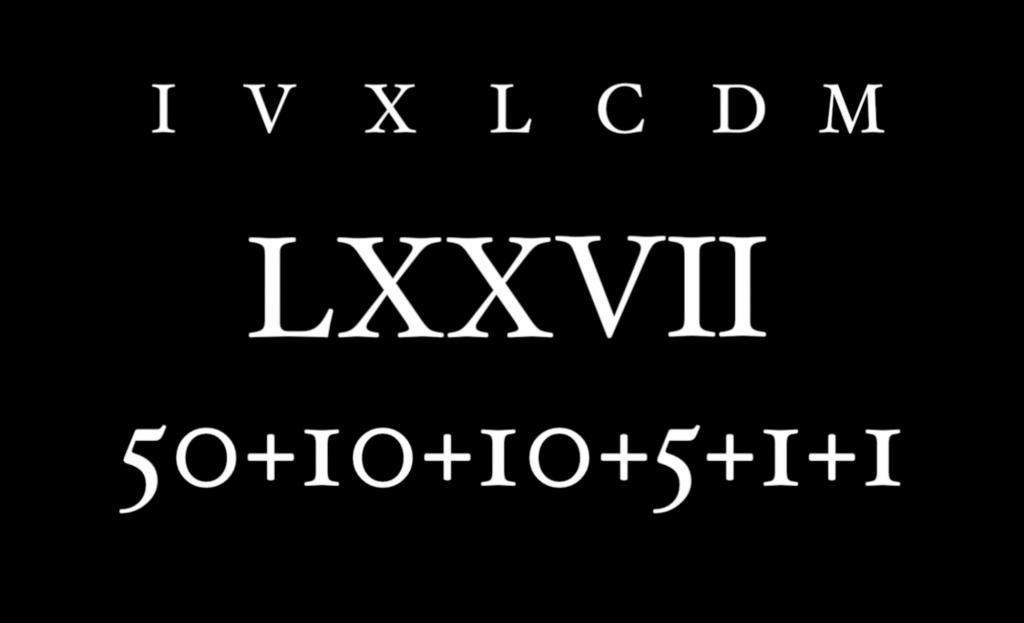
Как читать числа
При нумерации римскими цифрами числа формируются путем объединения различных букв и нахождения суммы этих значений. Цифры помещаются слева направо, а порядок цифр определяет, добавляются или вычитаются значения. Если одна или несколько букв помещаются после буквы большей ценности, значит, значение добавляют. Если буква помещается перед буквой большего значения, ее значение вычитают. Например, VI = 6, поскольку V больше I. Но IV = 4, так как I меньше V.
Существует ряд других правил, связанных с римскими цифрами. Например, нельзя использовать один и тот же символ более трех раз подряд. Когда дело доходит до вычитаемых сумм, вычитаются только степени 10, такие, как I, X или C, но не V или L. Например, 95 не является VC. 95 обозначается как XCV. XC равно 100 минус 10 или 90, поэтому XC плюс V или 90 плюс 5 равно 95.
Кроме того, только одно число может быть вычтено из другого. Например, 13 не является IIXV. Легко понять, как строится ход рассуждения: 15 минус 1 минус 1. Но, следуя правилу, вместо этого пишется XIII, или 10 плюс 3.
Кроме того, нельзя вычесть число из числа, которое больше исходного более чем в 10 раз. То есть, можно вычесть 1 из 10 (IX), но нельзя вычесть 1 из 100, нет такого числа, как IC. Вместо этого следует написать XCIX (XC + IX или 90 + 9). Для больших чисел в тысячах черта, помещенная над буквой или строкой букв, умножает значение цифры на 1000.

Самые большие числа
Самая старая примечательная надпись, содержащая римскую нумерацию, представляющую очень большие числа, находится на Ростральной колонне (ColumnaRostrata) - памятнике, воздвигнутом на Римском Форуме в ознаменование победы в 260 году до нашей эры над Карфагеном во время Первой Пунической войны. В этом столбце символ 100 000, который был ранней формой (((I))), повторялся 23 раза, составляя 2 300 000. Это иллюстрирует не только раннее римское использование повторяющихся символов, но и обычай, который распространяется на современность: использование (I) для 1000, (I)) для 10000, (((I))) для 100 000 и ((((I)))) за 1 000 000. Символ (I) для 1000 часто появляется в различных других формах, включая курсор ∞.
Недостатки римской системы нумерации
Эти цифры не лишены недостатков. Например, нет символа, обозначающего ноль, также нет возможности рассчитать дроби. Это затрудняло возможность развития общепринятой сложной математической системы, затрудняло торговлю. В конечном счете римские цифры уступили место более универсальной арабской системе, где числа читаются как одно число в последовательности. Например, 435 как четыреста тридцать пять.

Использование римских цифр
Когда Римская империя рухнула тысячу лет спустя, христианство продолжало использовать систему численности этой культуры.
На сегодняшний день римская нумерация появляется в научных работах и даже в титрах фильмов. Она используется в именованиях монархов, пап, кораблей и спортивных событий, таких как Олимпиада и Суперкубок.
Латинские цифры используются в астрономии для обозначения лун и в химии для обозначения групп периодической таблицы. Их можно увидеть в оглавлениях и рукописей, поскольку римские цифры верхнего и нижнего регистров разбивают информацию на легко организованную структуру. Теория музыки также использует римские цифры в своих обозначениях.
Эти виды использования объясняются скорее эстетическими соображениями, чем функциональными целями. Визуально цифры римской нумерации передают ощущение истории и вневременности, что особенно актуально в часах.

Прямое влияние Рима в течение такого длительного периода, превосходство его численной системы над любой другой более простой, известной в Европе до Х века, а также убедительная сила традиции объясняют сильную позицию, которую эта система поддерживала почти 2000 лет в торговле, в научной, богословской и художественной литературе. Это имело большое преимущество в том, что для массы пользователей необходимо было запомнить значения только четырех букв - V, X, L и C. Более того, было легче увидеть три в III, чем в 3, и увидеть восемь в VIII, чем в 8, и, соответственно, было проще добавить числа, то есть выполнить самую основную арифметическую операцию.