Мир, который нас окружает, находится в постоянном движении. Тем не менее существуют системы, которые могут находиться в относительном состоянии покоя и равновесия. Одной из них является рычаг. В данной статье рассмотрим, что он собой представляет с точки зрения физики, а также решим пару задач на условие равновесия рычага.
Что такое рычаг?
В физике рычагом называется простой механизм, состоящий из невесомой балки (доски) и одной опоры. Расположение опоры не является фиксированным, поэтому она может находиться ближе к одному из концов балки.
Являясь простым механизмом, рычаг служит для преобразования силы в путь, и наоборот. Несмотря на то, что сила и путь - это совершенно разные физические величины, они связаны друг с другом формулой работы. Чтобы поднять какой-либо груз, необходимо совершить некоторую работу. Сделать это можно двумя различными способами: приложить большую силу и переместить груз на небольшое расстояние или же подействовать незначительной силой, но при этом увеличить путь перемещения. Собственно, для этого и служит рычаг. Говоря коротко, этот механизм позволяет выиграть в пути и проиграть в силе или, наоборот, выиграть в силе, но проиграть в пути.

Действующие на рычаг силы
Данная статья посвящена условиям равновесия рычага. Любое равновесие в статике (раздел физики, изучающий тела в покое) предполагает наличие или отсутствие сил. Если рассматривать рычаг в свободном виде (невесомая балка и опора), то на него не действуют никакие силы, и он будет находиться в равновесии.
Когда с помощью рычага любого типа выполняют работу, то на него всегда действуют три силы. Перечислим их:
- Вес груза. Поскольку рассматриваемый механизм служит для подъема грузов, очевидно, что их вес придется преодолевать.
- Внешняя сила противодействия. Эта та сила, которую прикладывает человек или другая машина, чтобы противодействовать весу груза на балке рычага.
- Реакция опоры. Направление этой силы всегда перпендикулярно плоскости балки рычага. Сила реакции опоры направлена вверх.
Условие равновесия рычага предполагает рассмотрение не столько отмеченных действующих сил, сколько моментов сил, создаваемых ими.
Что такое момент силы
В физике моментом силы, или вращающим моментом, называют величину, равную произведению внешней силы на плечо. Плечом силы называют расстояние от точки приложения силы до оси вращения. Наличие последней является важным при расчете момента силы. Без наличия оси вращения нет никакого смысла говорить о моменте силы. Учитывая приведенное определение, можно записать следующее выражение для вращающего момента M:
M = F*d
Справедливости ради отметим, что момент силы в действительности - это векторная величина, тем не менее для понимания темы данной статьи достаточно знать, как рассчитывается модуль момента силы.
Помимо формулы выше, следует запомнить, что если сила F стремится повернуть систему так, что та начинает движение против часовой стрелки, то создаваемый момент считается положительным. Наоборот, стремление повернуть систему по ходу стрелки часов свидетельствует об отрицательном вращающем моменте.
Формула условия равновесия рычага
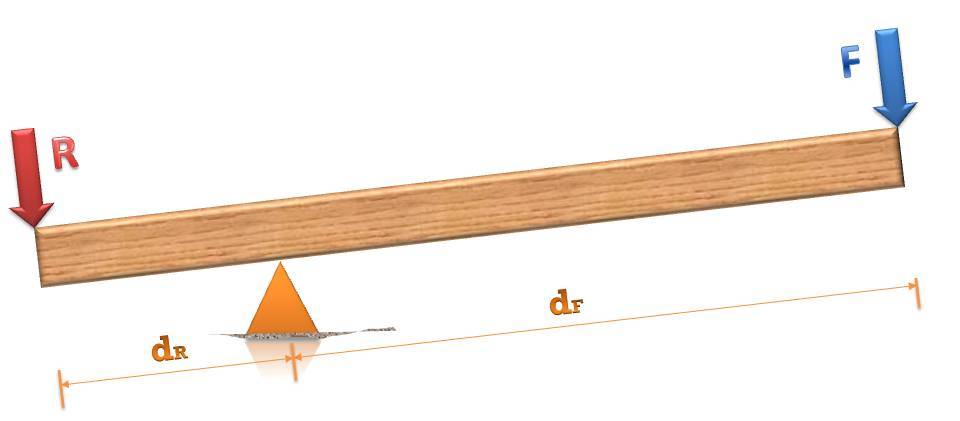
На рисунке ниже показан типичный рычаг, а также отмечены значения его правого и левого плеч. Внешняя сила обозначена буквой F, а вес груза, который следует поднять, обозначен буквой R.
В статике для того, чтобы система покоилась, необходимо выполнение двух условий:
- Сумма внешних сил, которые оказывают на систему воздействие, должна быть равна нулю.
- Сумма всех моментов упомянутых сил относительно любой оси должна быть нулевой.
Первое из названных условий означает отсутствие поступательного перемещения системы. Оно очевидно для рычага, поскольку его опора прочно стоит на полу или земле. Поэтому проверка условия равновесия рычага предполагает только проверку справедливости следующего выражения:
∑i=1nMi = 0
Поскольку в нашем случае действуют только три силы, перепишем эту формулу следующим образом:
R*dR - F*dF + N*0 = 0
Сила реакции опоры момента не создает. Последнее выражение перепишем в виде:
R*dR = F*dF
Это и есть условие равновесия рычага (в 7 классе общеобразовательных школ в курсе физики оно изучается). Формула показывает: если значение силы F будет больше веса груза R, то плечо dF должно быть меньше плеча dR. Последнее означает, что, прилагая большую силу в течение небольшого пути, мы можем переместить груз на большое расстояние. Справедлива и обратная ситуация, когда F<R и, соответственно, dF>dR. В этом случае выигрыш наблюдается в силе.
Задача со слоном и муравьем
Многим известно знаменитое высказывание Архимеда о возможности с помощью рычага сдвинуть целый земной шар. Это смелое заявление имеет физический смысл, если учесть формулу равновесия рычага, записанную выше. Оставим Архимеда и Землю в покое и решим несколько иную задачу, которая является не менее интересной.
Слона и муравья поместили на разные плечи рычага. Предположим, что центр масс слона находится в одном метре от опоры. На каком расстоянии от опоры должен находиться муравей, чтобы уравновесить слона?
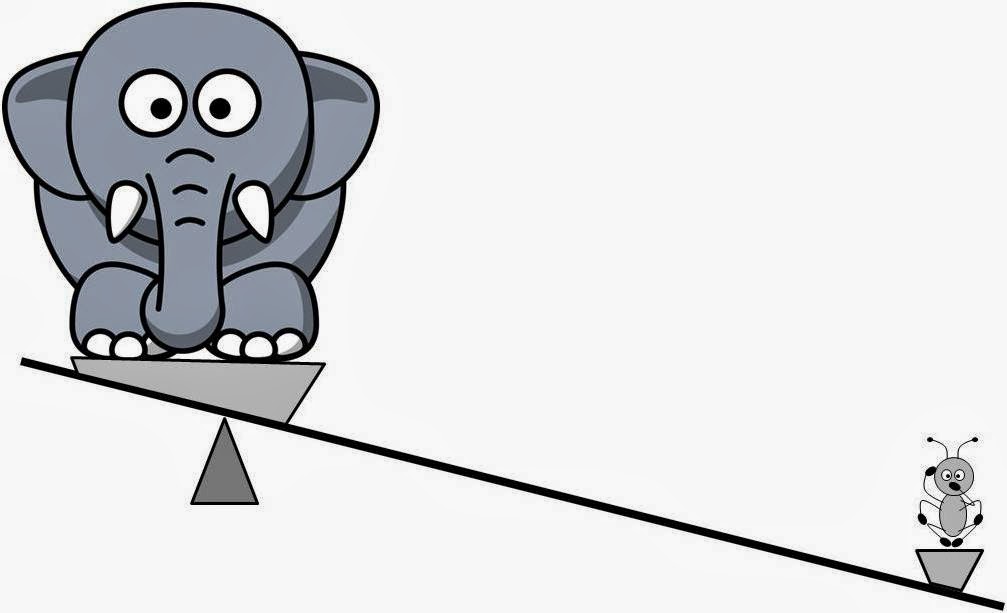
Чтобы ответить на вопрос задачи, обратимся к табличным данным о массах рассматриваемых животных. Массу муравья возьмем 5 мг (5*10-6 кг), массу слона будем считать равной 5000 кг. Используя формулу равновесия рычага, получаем:
5000*1 = 5*10-6*x =>
x = 5000/(5*10-6) = 109 м.
Муравей действительно может уравновесить слона, но для этого он должен располагаться от опоры рычага на расстоянии 1 миллион километров, что соответствует 1/150 расстояния от Земли до Солнца!
Задача с опорой на конце балки
Как было отмечено выше, у рычага опора под балкой может располагаться в любом месте. Предположим, что она находится вблизи одного из концов балки. Такой рычаг имеет единственное плечо, показанное ниже на рисунке.

Предположим, что груз (красная стрелка) имеет массу 50 кг и расположен точно посередине плеча рычага. Какой величины должна быть внешняя сила F (синяя стрелка), которая приложена к концу плеча, чтобы уравновесить этот груз?
Обозначим длину плеча рычага буквой d. Тогда можно записать условие равновесия в следующем виде:
F*d = R*d/2 =>
F = m*g/2 = 50*9,81/2 = 245,25 Н
Таким образом, величина приложенной силы должна быть в два раза меньше веса груза.

Данный тип рычага используется в таких изобретениях, как ручная тачка для перемещения грузов или орехокол.



























