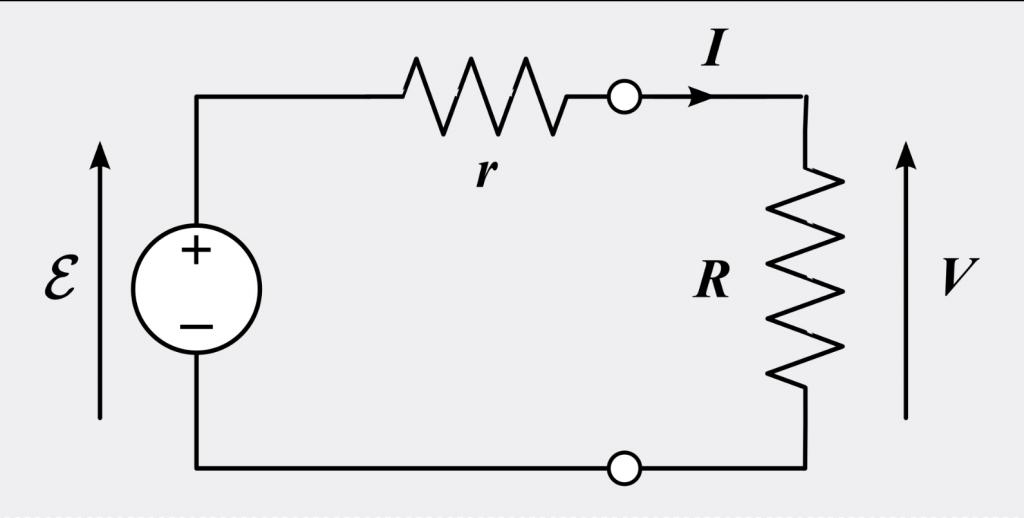
Закон Ома в дифференциальной и интегральной форме гласит, что ток через проводник между двумя точками прямо пропорционально от напряжения на две точки. Уравнение с константой выглядит так:
I = V/R,
где I - это точка тока через проводник в единицы ампер, V (Вольт) - напряжение, измеренное при помощи проводника в единицах вольт, R - сопротивление проводимого материала в Омах. Более конкретно, закон Ома гласит, что R в этом отношении является постоянной, независимой от тока.
Что можно понимать под "Законом Ома"?
Закон Ома в дифференциальной и интегральной форме является эмпирическим соотношением, которое точно описывает проводимость подавляющего большинства проводниковых материалов. Однако некоторые материалы не подчиняются закону Ома, называются они "неомическими". Закон был назван в честь ученого Георга Ома, который опубликовал его в 1827 году. Он описывает измерения напряжения и тока с помощью простых электрических цепей, содержащих различные длины провода. Ом объяснил свои экспериментальные результаты с несколько более сложным уравнением, чем современная форма выше.
Понятие закона Ома в диф. форме также применяется для обозначения различных обобщений, например, векторная форма его используется в электромагнетизме и материаловедении:
J=σE,
где J - количество электрических частиц в конкретном месте резистивного материала, е - электрическое поле в этом месте и σ (сигма)- это материал, зависящий от параметра проводимости. Густав Кирхгоф сформулировал закон именно так.
История

История
В январе 1781 Генри Кавендиш экспериментировал с лейденской банкой и стеклянной трубой различного диаметра, наполненной раствором соли. Кавендиш писал, что скорость изменяется непосредственно как степень электрификации. Изначально результаты были неизвестны научному сообществу. Но Максвелл опубликовал их в 1879 году.
Ом сделал свою работу на сопротивлении в 1825 и 1826 годах и опубликовал свои результаты в 1827 году в книге "Гальваническая цепь доказана математически". Вдохновлялся он работой французского математика Фурье, которая описывала теплопроводность. Для экспериментов он изначально использовал гальванические сваи, но позже перешел к термопарам, что смогло обеспечить более стабилизированный источник напряжения тока. Оперировался он понятиями внутреннего сопротивления и постоянного напряжения тока.
Также в этих опытах использовался гальванометр для измерения тока, так как напряжение между клеммами термопары пропорционально температуре соединения. Затем он добавил тестовые провода различной длины, диаметра и материала для завершения схемы. Он обнаружил, что его данные могут быть смоделированы с помощью следующего уравнения
x= a/b + l,
где x - показания измерительного прибора, l - длина испытательного проводника, a -зависящая от температуры соединения термопары, b - константа (постоянная) всего уравнения. Ом доказал свой закон на основе этих вычислений пропорциональности и опубликовал свои результаты.
Важность закона Ома
Закон Ома в дифференциальной и интегральной форме, вероятно, являлся самым важным из ранних описаний физики электричества. Сегодня же мы считаем это почти очевидным, но, когда Ом впервые опубликовал свои работы, это было не так. Критики отнеслись к его трактовке с враждебностью. Они называли его работы "голыми фантазиями", а немецкий министр образования заявил, что "профессор, который проповедует такую ересь, недостоин преподавать науку".
Преобладающая в то время в Германии научная философия утверждала, что нет необходимости проводить эксперименты, чтобы развить понимание природы. Кроме того, брат Геогра, Мартин, математик по профессии, боролся с немецкой образовательной системой. Эти факторы препятствовали принятию работы Ома, и его работа не получила широкого признания до 1840-х годов. Тем не менее Ом получил признание за его вклад в науку задолго до его смерти.
Закон Ома в дифференциальной и интегральной форме представляет собой эмпирический закон, обобщение результатов многих экспериментов, которые показали, что ток примерно пропорционален напряжению электрического поля для большинства материалов. Он является менее фундаментальным, чем уравнения Максвелла, и подходит не во всех ситуациях. Любой материал будет разрушаться под силой достаточного электрического поля.
Закон Ома был соблюден на широком диапазоне шкал. В начале 20-го века закон Ома не рассматривался в атомном масштабе, однако эксперименты подтверждают обратное.
Квантовое начало

Зависимость плотности тока от приложенного электрического поля имеет принципиально квантово-механический характер (классическая квантовая проходимость). Качественное описание закона Ома может быть основано на классической механике с помощью модели Друде, разработанной немецким физиком Паулем Друде в 1900 году. Из-за этого закон Ома имеет множество форм, например, так называемый закон Ома в дифференциальной форме.
Другие формы закона Ома
Закон Ома в дифференциальной форме является крайне важным понятием для электротехники/электроники, поскольку он описывает как напряжение тока, так и сопротивление. Все это взаимосвязано на макроскопическом уровне. Изучая электрические свойства на макро- или микроскопическом уровне, используется более связанное уравнение, которое можно назвать "уравнением Ома", имеющее переменные, которые тесно связаны со скалярными переменными V, I и R закона Ома, но которые являются постоянной функцией положения в проводнике.
Эффект магнетизма

Если присутствует внешнее магнитное поле (B) и проводник не находится в покое, но движется со скоростью V, то необходимо добавить дополнительную переменную, чтобы учесть ток, индуцированный силой Лоренца на носителях заряда. Также это называется законом Ома интегральной формы:
J= σ (E + v * B).
В системе покоя движущегося проводника этот термин выпадает, потому что V = 0. Там нет никакого сопротивления, поскольку электрическое поле в системе покоя отличается от E-поля в лабораторной системе: E'= E + v × B. Электрические и магнитные поля относительны. Если J (ток) является переменным из-за того, что приложенное напряжение или E-поле изменяются во времени, то к сопротивлению необходимо добавить реактивное сопротивление, чтобы учесть самоиндукцию. Реактивное сопротивление может быть сильным, если частота высокая или проводник намотан.



























