Тригонометрия - математическая наука о тригонометрических функциях sin и cos. Эти отношения - базовые понятия, без их понимания не получится изучать что-то новое в этой области. Это не сложно, главное понимать, откуда берутся значения косинусов и синусов и как их рассчитать.
Из истории появления
В работах древнегреческих математиков уже в III веке до нашей эры встречаются отношения отрезков треугольников. В древнем Риме их исследовал Менелай. Математик Ариабхата из Индии также дал определения этим понятиям. Вычисления синуса он связывал с "архадживами" (дословный перевод - половина тетивы лука) - полухордами окружности. Позднее понятие сократилось до слова "джива". Арабские математики использовали термин "джайб" (выпуклость).

А что насчет cos? Это отношение значительно моложе. Понятие представляет собой сокращение от латинского выражения completely sinus, что в переводе звучит как дополнительный синус (синус дополнительной дуги).
Современные краткие латинские обозначения sin и cos введены Уильямом Отредом в VII веке и закреплены в трудах Эйлера.
Что такое прямоугольный треугольник?
Поскольку sin и cos - это отношения величин этой фигуры, то необходимо знать, что она собой представляет. Это вид треугольника, у которого один из углов прямой, то есть составляет 90 градусов. Катетами называют стороны, прилежащие к прямому углу (лежат напротив острых), а гипотенузой - противолежащую сторону.
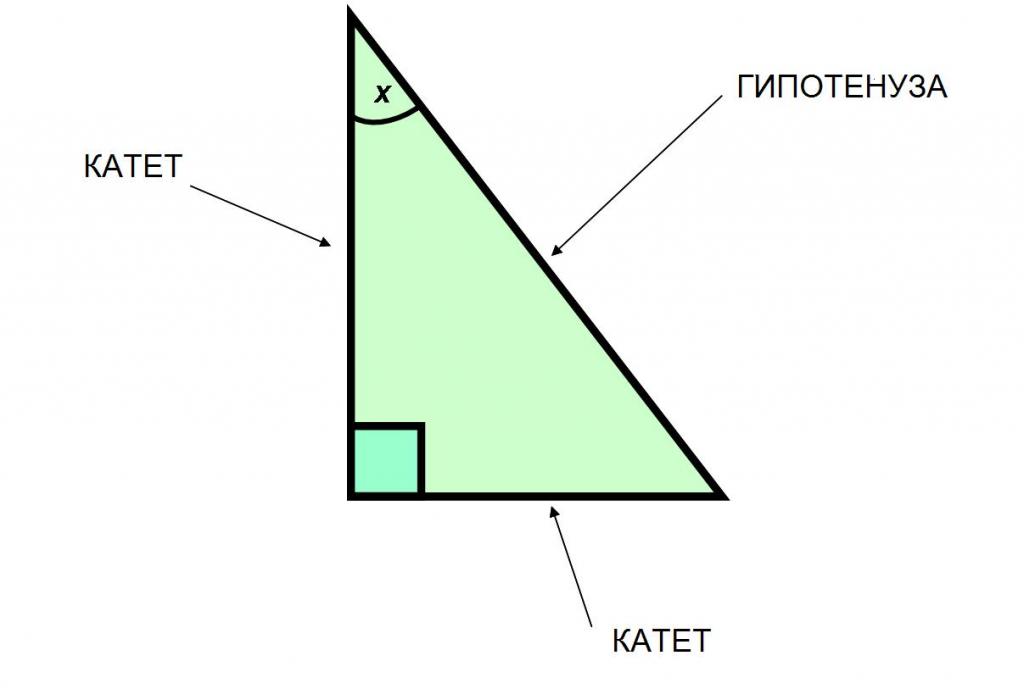
Они связаны между собой теоремой Пифагора.
Определения синуса и косинуса
sin - это отношение противолежащего катета к гипотенузе.
cos - это отношение прилежащего катета к гипотенузе.
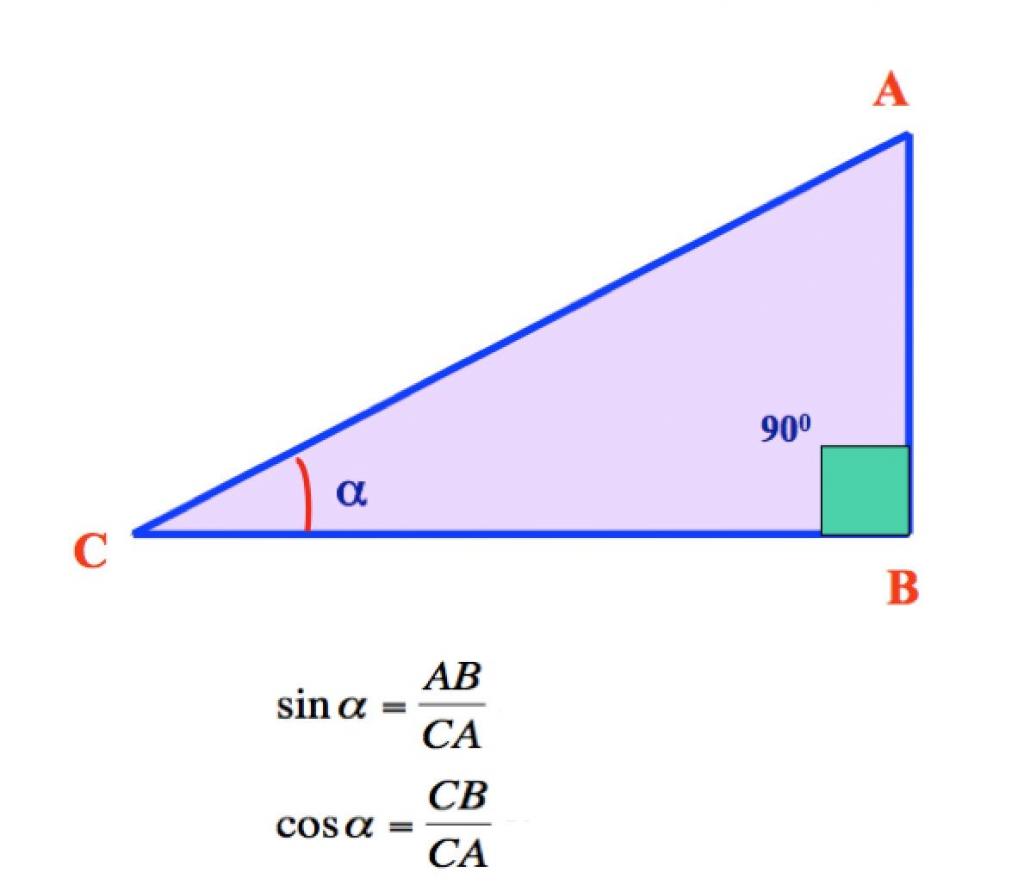
Зная численные значения сторон треугольника можно определить обе эти величины.
Если рассмотреть единичную окружность с центром в точке (0,0) декартовой системы координат, тогда, взяв точку на оси абсцисс и повернув ее на острый угол альфа, опустим перпендикуляр на ось абсцисс. Длина катета, прилежащего к гипотенузе в полученном прямоугольном треугольнике, будет равна абсциссе точки.
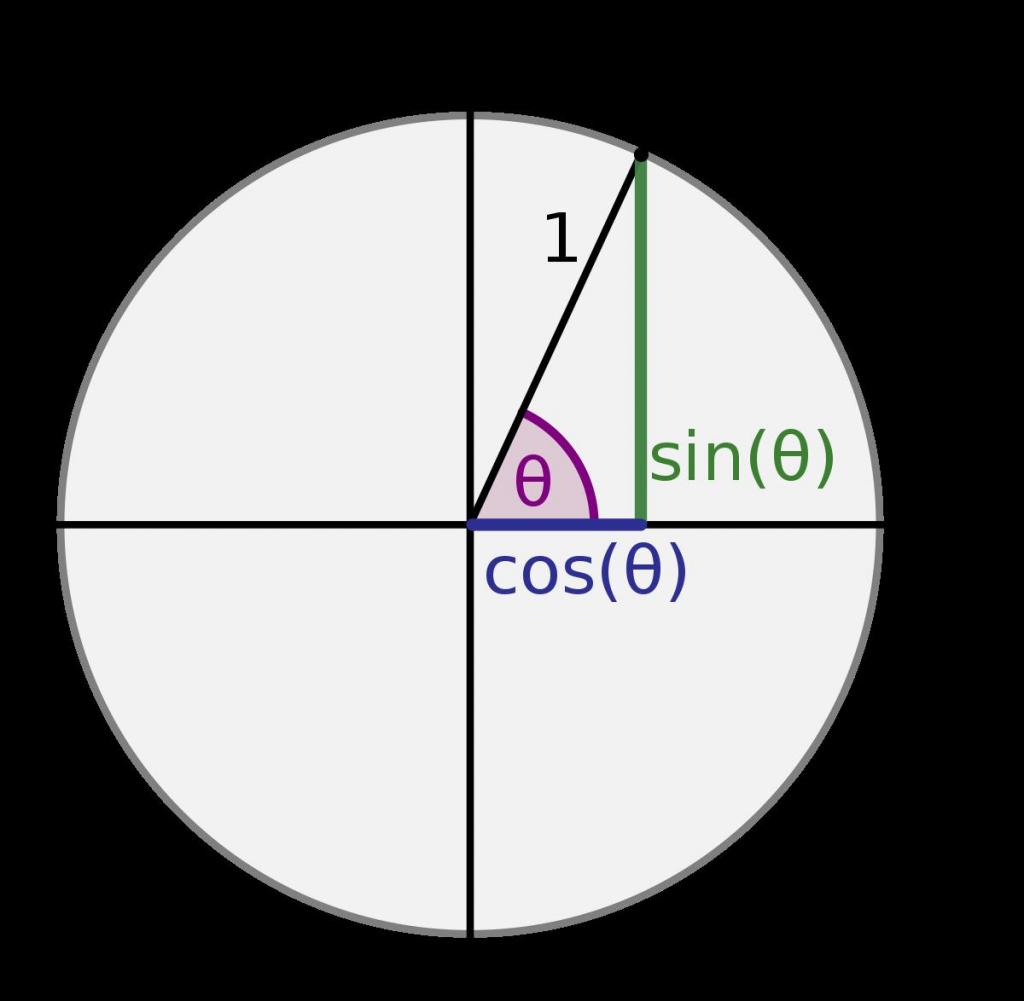
Следовательно, определение через отношение сторон cos(sin) острого угла в этой фигуре эквивалентно нахождению косинуса (синуса) угла поворота при альфа, лежащем в пределах от 0 до 90 градусов.
Для чего нужны данные тригонометрические функции?
Известно, что сумма углов в прямоугольном треугольнике равна 180 градусам. Значит, зная два угла, можно найти третий. С помощью теоремы Пифагора находят значение любой из сторон по двум другим. А их отношения через sin и cos помогут, если известен один угол и одна любая сторона.
Вопрос решения такой задачи возник при составлении карт звездного неба, когда точно невозможно было измерить все величины.
С другой стороны, отношения sin и cos - это тригонометрические функции угла. Если известно его значение, то с помощью специальных таблиц получится найти все необходимые показатели.

























