Четырехугольник - удивительная геометрическая фигура, обладающая множеством полезных свойств. Давайте разберемся, что это за фигура, как вычислить ее площадь и периметр, и где все это может пригодиться на практике.
Определение произвольного четырехугольника
Произвольный четырехугольник - это четырехугольник, у которого нет каких-либо дополнительных свойств, отличающих его от других четырехугольников. Иными словами, это обобщенное название для всех возможных четырехугольников.
Напомним, что четырехугольник — это геометрическая фигура (многоугольник), состоящая из четырех точек (вершин), никакие три из которых не лежат на одной прямой, и четырех отрезков (сторон), последовательно соединяющих эти точки.
Существует много разновидностей четырехугольников - параллелограммы, трапеции, прямоугольники, ромбы, квадраты и другие. У каждого из них есть свои отличительные свойства. А произвольный четырехугольник просто обозначает четырехугольник без каких-либо особых свойств.
Вычисление площади произвольного четырехугольника
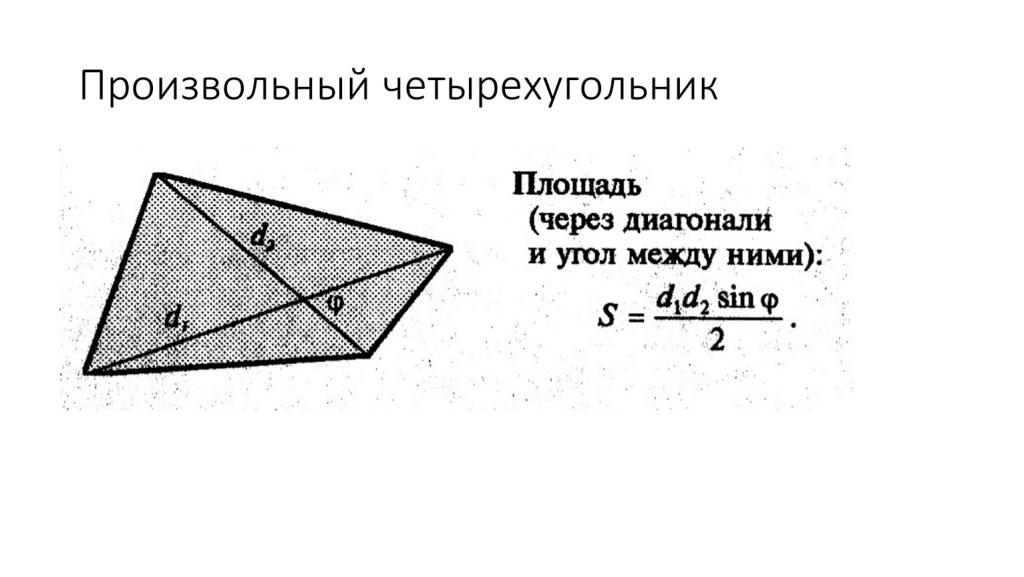
Для вычисления площади произвольного четырехугольника используется общая формула:
S= 1/2 d1d2 sinα
где d1 и d2 - длины диагоналей четырехугольника, а α - угол между ними.
Также можно воспользоваться формулой Герона для вычисления площади треугольника. Для этого произвольный четырехугольник разбивают на два треугольника по диагонали, вычисляют площадь каждого треугольника по формуле Герона, и складывают результаты:
S = (p (p - a1) (p - b1) (p - c)) + (p (p - a2) (p - b2) (p - c)
где p - полупериметр треугольника, а a1, а2, b1, b2 - длины его сторон, с - общая сторона
Вычисление периметра произвольного четырехугольника
Помимо площади, для четырехугольника можно вычислить его периметр - сумму длин всех сторон:
P = a + b + c + d
где a, b, c и d - длины сторон четырехугольника.
Эта формула одинакова для любого четырехугольника, в том числе и произвольного. Рассмотрим пример: пусть у нас есть произвольный четырехугольник со сторонами 7 см, 4 см, 12 см и 9 см. Тогда его периметр равен:
P = 7 + 4 + 12 + 9 = 32 см
Применение свойств произвольного четырехугольника
Хотя у произвольного четырехугольника и нет каких-то особых свойств, те общие свойства, которые присущи любому четырехугольнику, позволяют применять его в различных областях.
Использование в геометрических задачах
Например, в геометрических задачах на вычисление площадей, нахождение углов, построение сечений и многое другое. Для этого используют такие свойства:
- Сумма всех углов четырехугольника равна 360°
- Сумма длин любых трех сторон больше длины четвертой стороны
- Диагонали делят четырехугольник на треугольники
Эти и другие свойства позволяют решать множество задач с участием произвольного четырехугольника.
Применение в архитектуре и строительстве
В архитектуре четырехугольные формы часто используются при проектировании зданий и отдельных элементов. Например:
- Прямоугольные комнаты и помещения
- Четырехугольные опорные балки
- Четырехскатные крыши
При расчетах в таких конструкциях удобно рассматривать их как произвольные четырехугольники и использовать соответствующие формулы для вычислений.
Интересные факты о произвольном четырехугольнике

Помимо полезных свойств, произвольный четырехугольник иногда появляется в занимательных фактах и неожиданных областях:
Произвольный четырехугольник в живописи
Художники эпохи Возрождения часто использовали в своих картинах математические формы, в том числе различные четырехугольники. Они могли обозначать гармонию, соразмерность или другие философские понятия.
Загадки с произвольным четырехугольником
Существуют интересные головоломки и задачи со спичками, в которых нужно сложить из данного количества спичек произвольный четырехугольник с заданным условием. Например, используя 8 спичек, построить четырехугольник с диагоналями одинаковой длины.
Обобщения и аналоги произвольного четырехугольника
Концепция произвольного четырехугольника позволяет сделать некоторые обобщения на другие геометрические фигуры и математические объекты:
Многоугольники большего порядка
Понятие "произвольный" можно обобщить и на многоугольники, состоящие из большего числа сторон - пяти, шести и т.д. Такие фигуры тоже можно рассматривать как обобщенные многоугольники без дополнительных свойств.
Произвольный многогранник
В пространственной геометрии аналогом четырехугольника служит четырехгранник. По аналогии можно ввести понятие произвольного четырехгранника и изучать его общие свойства.
Произвольная фигура в комбинаторике
В комбинаторике и теории графов под произвольной фигурой понимают некоторое множество элементов без заданной структуры. Это похоже на концепцию произвольного четырехугольника в геометрии.
Перспективы дальнейшего изучения произвольного четырехугольника
Несмотря на кажущуюся простоту, произвольный четырехугольник обладает глубокой математической структурой, которую можно исследовать:
- Изучение симметрий и самоподобия
- Обобщения на криволинейные четырехугольники
- Связи с другими математическими объектами
Также можно находить новые практические применения четырехугольников в физике, архитектуре и других областях. Поле исследований здесь действительно обширно!























