Измерение отрезков - важный навык, необходимый как при решении математических задач, так и в повседневной жизни. Чтобы измерить отрезок, нужно выбрать единицу измерения и определить, сколько раз эта единица укладывается в данном отрезке. Для измерения используют такие инструменты, как линейка и циркуль.
В данной статье мы рассмотрим основные способы измерения отрезков с помощью линейки и циркуля. А также разберем примеры практических задач, решение которых поможет лучше закрепить навыки измерения отрезков.
Построение отрезка заданной длины
Измерение и построение отрезков с заданной длиной - важный практический навык, который необходимо развивать на уроках математики. Для измерения отрезков используются такие инструменты, как линейка, циркуль, миллиметровая бумага. Чтобы построить отрезок заданной длины, нужно выполнить следующие действия:
- Взять линейку и отметить на ней точку А, от которой будем откладывать отрезок.
- Приложить линейку к точке А и отложить на ней требуемое число сантиметров или миллиметров, обозначив конечную точку отрезка В.
- Соединить точки А и В.
Также отрезок можно построить с помощью циркуля. Для этого нужно установить размер ножек по линейке, затем одну ножку приложить к начальной точке А, а другой начертить точку В. Затем соединить точки.
При выполнении измерений и построений важно соблюдать аккуратность и точность. Эти навыки помогут решать практические задачи и вырабатывают внимательность.
Сравнение отрезков по длине
После того как мы научились измерять отрезки, важно понять, как можно их сравнивать. Для этого существуют разные способы.
Первый способ - непосредственное наложение отрезков друг на друга. Если концы отрезков совпадают, то они равны. Если один отрезок выступает за пределы другого, то он длиннее.
Второй способ - измерение каждого отрезка линейкой и сравнение полученных числовых значений. Тот отрезок, длина которого больше, является длиннее.
Третий способ - использование циркуля или другого измерительного инструмента. Сначала устанавливается расстояние по одному отрезку, затем проверяется, укладывается ли это расстояние целиком на другом отрезке. Если да - отрезки равны, если нет - один отрезок длиннее другого.
При измерении отрезков и их сравнении важно быть внимательным и аккуратным, чтобы получить точный результат. Эти навыки пригодятся для решения многих практических задач.
Решение практических задач на измерение отрезков
Измерение отрезков - это важный навык, который позволяет решать множество практических задач:
- Определение расстояния между двумя точками на местности.
- Расчет необходимой длины ткани для пошива одежды.
- Вычисление периметра различных фигур.
Рассмотрим примеры задач на измерение отрезков:
Задача 1. Высота дерева на чертеже изображена отрезком D. Найдите действительную высоту дерева, если известно, что 1 см на чертеже соответствует 2 м в действительности.
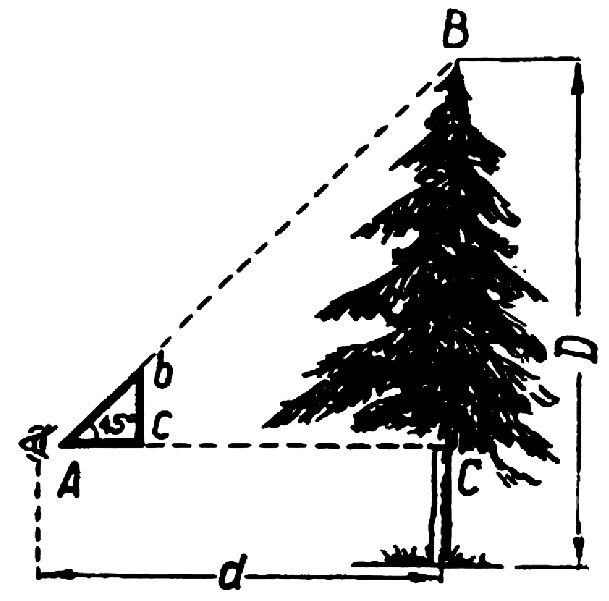
Решение. Сначала находим высоту дерева на чертеже с помощью линейки. У нас вышло 12 см. Далее по условию задачи 1 см = 2 м. Значит, отрезок D длиной 12 см будет равен 12 · 2 = 24 м. Ответ: 24 м.
Задача 2. Садовая дорожка, изображенная на плане отрезком CD. Найдите длину настоящей дорожки, если известно, что в масштабе плана 1 : 100.
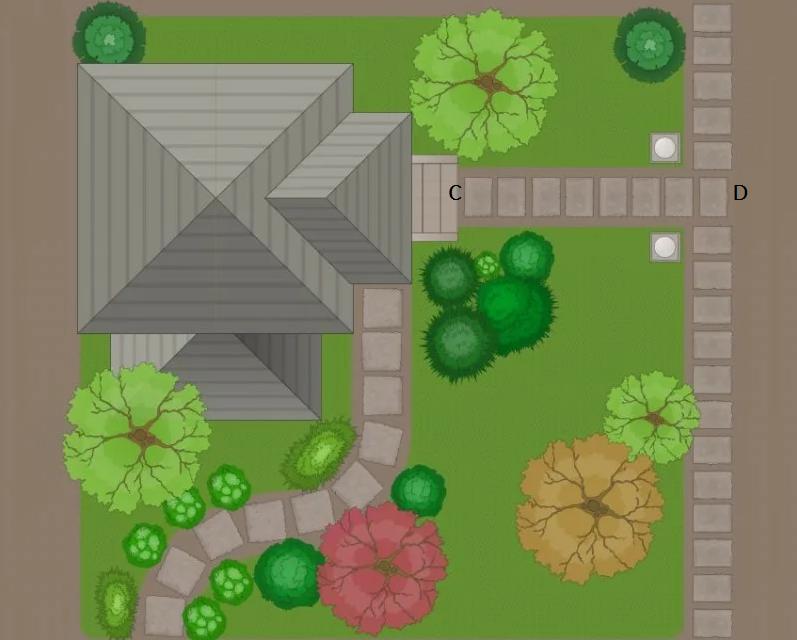
Решение. Сначала находим длину дорожки на чертеже с помощью линейки. У нас вышло 8 см. В масштабе 1 : 100 каждый 1 см плана соответствует 100 см в действительности. Значит, отрезок CD длиной 18 см будет равен 8 · 100 = 800 см = 8 м. Ответ: 8 м.
Такие задачи учат применять навыки измерения отрезков для решения практических ситуаций. Это развивает сообразительность и умение работать с масштабом.
Развитие навыков измерения отрезков
Чтобы хорошо овладеть навыками измерения отрезков, нужно регулярно тренироваться выполняя следующие упражнения:
- Измерь заданные отрезки и запиши их длины.
- Построй отрезки заданной длины с помощью линейки и циркуля.
- Сравни отрезки, измерь каждый и определи, какой длиннее.
- Вычисли периметр данной фигуры, предварительно измерив все ее стороны.
Также полезно решать различные практические задачи, в которых применяются навыки измерения, например:
- Определить, какое расстояние пробежал спортсмен, если на плане его путь изображен отрезком длиной 5 см, а в масштабе 1 см соответствует 20 м.
- Найти ширину пруда, если на карте она равна отрезку 7 см, а 1 см соответствует 15 м.
Чем чаще ребенок будет выполнять подобные задания на измерение отрезков, тем лучше он овладеет этим важным навыком. А это в свою очередь поможет ему решать множество задач из окружающей жизни.























