Ломаные линии - неотъемлемая часть нашей жизни. Мы видим их в дорожной разметке, в чертежах зданий, в графиках биржевых котировок. Но мало кто задумывается, из чего состоят ломаные и как устроены их звенья.
Что такое ломаная линия и ее элементы
Ломаная линия - это линия, составленная из отдельных отрезков, называемых звеньями. Звенья соединяются в определенной последовательности в точках, которые называются вершинами ломаной
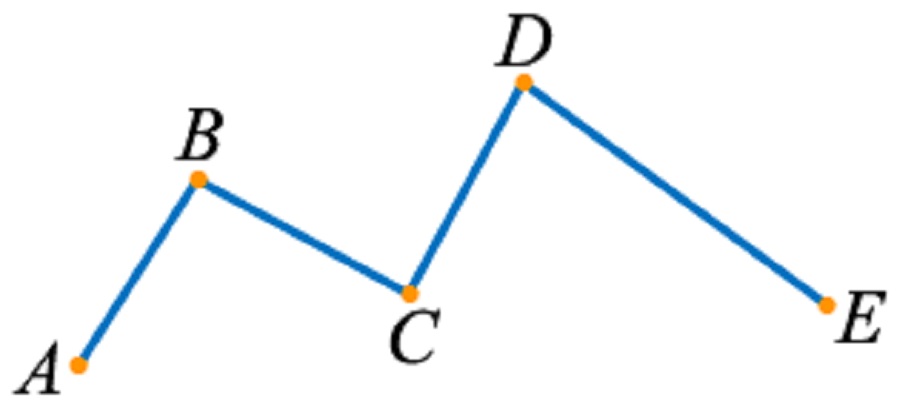
Например, на рисунке изображена ломаная ABCDE, состоящая из звеньев AB, BC, CD и DE. Точки A, B, C, D и E - это вершины данной ломаной.
Количество звеньев в ломаной всегда на единицу меньше, чем количество ее вершин. Это важное свойство помогает при вычислениях.
Существуют разные виды ломаных линий. Они могут быть замкнутыми или незамкнутыми, самопересекающимися или несамопересекающимися. Но в любом случае, именно звенья задают форму ломаной.
Свойства звеньев ломаной
У звеньев ломаной есть несколько важных свойств, которые влияют на общую форму линии:
- Длина звеньев.
- Форма звеньев (прямые или кривые).
- Углы между смежными звеньями.
Длина звеньев может быть одинаковой или разной. Например, если все звенья равны, ломаная называется правильной .
Форма звеньев тоже бывает разной - они могут быть прямыми отрезками или кривыми линиями. Прямые звенья проще для изучения.
Углы между смежными звеньями определяют "резкость" поворотов ломаной. Чем острее углы, тем резче ломаная меняет направление.
Комбинируя звенья с разными свойствами, можно построить ломаные самых причудливых форм.
Классификация ломаных линий по звеньям
В зависимости от свойств звеньев, ломаные линии делят на следующие типы:
- Ломаные с равными и неравными звеньями.
- Ломаные с прямыми и кривыми звеньями.
- Замкнутые и незамкнутые ломаные.
- Самопересекающиеся ломаные и их разновидности.
Рассмотрим некоторые интересные виды таких ломаных:
- Ломаная с равными звеньями называется правильной . У нее есть интересные свойства, связанные с симметрией. Например, правильный n-угольник - это правильная замкнутая ломаная из n равных звеньев. Такие многоугольники часто встречаются в орнаментах.
- Звездчатые ломаные с самопересечениями можно построить из звеньев разной длины, расположив их симметрично. У таких ломаных есть практическое применение - например, при проектировании радиоантенн.
- Фрактальные ломаные строятся путем многократного повторения одних и тех же звеньев. Получаются удивительные самоподобные структуры, похожие на побеги папоротника или разветвления кровеносных сосудов.
Как видите, вариантов ломаных линий великое множество. И это еще не предел, ведь можно изобретать все новые комбинации звеньев.
Давайте рассмотрим несколько конкретных примеров, где звенья ломаных линий играют важную роль.

Применение звеньев ломаной в геометрии
В геометрии звенья ломаных используются повсеместно - например, при построении различных многоугольников. Соединяя отрезки в определенном порядке, можно получать треугольники, четырехугольники, пятиугольники и так далее. У каждого многоугольника свои интересные свойства в зависимости от длин звеньев и углов между ними.
Если соединить конечные точки незамкнутой ломаной отрезком, то получится многоугольник. Иногда для удобства ломаные используют вместо сложных кривых, например при вычислении площадей фигур или длин кривых.
Звенья ломаных в инженерных расчетах
В строительстве, машиностроении и других отраслях техники приходится моделировать и рассчитывать сложные объекты со множеством элементов. Разбиение конструкции на отдельные звенья-отрезки часто упрощает такие расчеты.
Например, при расчете металлической фермы ее можно заменить ломаной линией для упрощения вычислений. Каждое звено будет соответствовать отдельной стержневой конструкции в ферме.
Моделирование физических процессов с помощью ломаных
Ломаные линии позволяют удобно моделировать объекты и процессы в физике, химии, экономике. Например, траекторию движения тела можно заменить на ломаную для приближенных вычислений.
Графики биржевых котировок или зависимостей различных физических величин часто строятся с помощью ломаных линий. Каждое звено на таком графике отражает изменение показателя на определенном промежутке времени.

Применение звеньев ломаной в компьютерной графике
Современные компьютерные технологии активно используют ломаные линии и их звенья. В векторной графике сложные кривые часто аппроксимируются ломаными для упрощения расчетов и отображения.
Трехмерные модели объектов в компьютерных играх и приложениях тоже создаются из отдельных многоугольников. Их грани математически представляют собой звенья замкнутых ломаных.
Любопытные факты про звенья ломаных линий
В заключение приведем несколько интересных фактов, связанных со звеньями ломаных:
- Звезды и снежинки имеют форму ломаных линий с самопересечениями.
- В орнаментах часто встречаются правильные многоугольники, построенные из равных звеньев.
- При проектировании зданий и сооружений используют ломаные для упрощения чертежей.
- Художники пользуются ломаными линиями, чтобы передать острые углы и точки поворота.
Как видите, звенья ломаных применяются в самых разнообразных областях. А сколько еще интересных фактов можно открыть, если присмотреться к этим линиям внимательнее.


























