Секущая - удивительно полезная вещь в геометрии. Она помогает решать множество задач, связанных с построением различных фигур, вычислением расстояний и углов. Давайте разберемся, что же такое секущая и где она применяется.

Что такое секущая
Секущая — это прямая линия, которая пересекает некую кривую (окружность, эллипс и т.д.) в двух и более точках. В отличие от касательной, у секущей с кривой всегда несколько общих точек.
секущая это прямая, пересекающая кривую в 2 точках
То есть секущая как бы "рассекает" кривую пополам, отсюда и название. Это важное свойство секущей часто используется при решении геометрических задач.
Виды секущих
Различают несколько основных видов секущих:
- Секущая к окружности
- Секущая к эллипсу, параболе, гиперболе и др. кривым
- Секущая плоскости
- Секущая прямого угла
Рассмотрим некоторые из них подробнее.
Секущая к окружности
Это наиболее распространенный вид секущей в элементарной геометрии. секущая к окружности это прямая, проходящая через окружность в двух точках и делящая ее пополам.
Такая секущая используется, к примеру, при вычислении расстояний между точками окружности или при доказательстве различных теорем и свойств.
Секущая плоскости
Секущая плоскость — это плоскость, которая пересекает некую исходную плоскость по прямой линии. Такие секущие часто применяются в стереометрии.
С помощью секущих плоскостей можно, к примеру, находить сечения различных многогранников или вычислять углы между плоскостями.
Теперь, когда мы выяснили, что такое секущая и какие бывают ее виды, давайте перейдем к более полезным вещам — применению секущих при решении задач. Секущие очень удобно использовать при решении целого класса геометрических задач. Рассмотрим несколько примеров.
Нахождение расстояний и длин отрезков
Допустим, нужно найти расстояние между двумя точками окружности. Для этого можно воспользоваться секущей, проходящей через эти точки:
Как видно из рисунка, искомое расстояние равно длине отрезка секущей между точками пересечения. Аналогично находятся длины хорд и других отрезков.
Вычисление углов
Зная свойства секущей, можно вычислять величины разных углов. Например, если секущая делит хорду пополам (проходит через середину хорды), то угол между секущей и хордой равен 90 градусов.
Также при помощи секущих доказываются многие теоремы о вписанных, центральных и периферийных углах.
Еще одно важное применение секущей — это построение касательной к кривой в данной точке. Секущая, проходящая все ближе к этой точке, в пределе становится касательной.
Как видите, секущая — очень полезный инструмент, который помогает решать массу задач. А это лишь некоторые примеры, на самом деле областей применения секущей значительно больше.
Другие применения секущей
Помимо описанных выше задач, секущие успешно используются еще во многих областях геометрии. Давайте рассмотрим некоторые из них.
Задача: построить равнобедренный треугольник по двум сторонам и углу между ними. Решение: проводим через концы отрезков, задающих стороны, произвольную секущую. Затем откладываем на ней отрезок, равный третьей стороне. Получаем точку, через которую проводим требуемый треугольник.
Деление отрезков
Секущая позволяет делить отрезки в заданном отношении без использования циркуля. Для этого достаточно построить треугольник с помощью двух параллельных прямых и соединяющей их секущей.
Графический метод с использованием секущих удобен для нахождения корней многочленов, решения тригонометрических и других уравнений и неравенств. Секущие позволяют наглядно определить точки пересечения графиков.
Задачи на максимум и минимум
Для нахождения экстремумов функции часто используют секущую, параллельную оси абсцисс. Опуская и поднимая ее, находим точки перегиба графика, в которых функция принимает наибольшее и наименьшее значения.
В пространственной геометрии секущие плоскости позволяют находить сечения многогранников, цилиндров, конусов и других тел. Анализируя форму сечений, можно делать выводы о свойствах самих тел.
Преобразования плоскости
Теория движения плоскости при параллельном переносе и симметрии также опирается на использование вспомогательных секущих для доказательства соответствующих теорем и нахождения образов фигур.
Как видим, области применения секущих в геометрии чрезвычайно разнообразны. Это объясняет важную роль, которую секущие играют в решении геометрических задач самого разного типа.
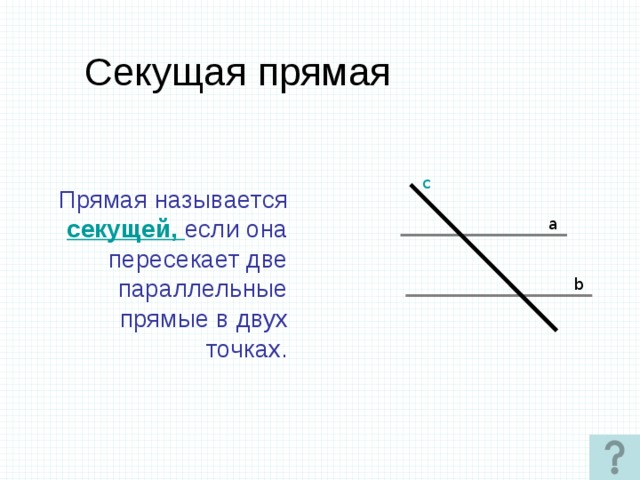
Свойства и теоремы о секущих
Секущие обладают множеством интересных свойств, на основе которых доказано немало важных теорем. Давайте познакомимся с некоторыми из них.
Эта теорема гласит: если серия секущих имеет общую точку с кривой, а все прочие точки пересечения стремятся к этой общей точке, то предел положения секущих есть касательная к кривой в данной общей точке.
Теорема о произведении отрезков
Для секущей, проходящей через вершину угла и выходящей за его стороны, выполняется равенство: произведение расстояний от точки пересечения с одной стороной до ее конца на аналогичное расстояние для другой стороны есть величина постоянная.
Если секущая параллельно переносится вдоль кривой на некоторое расстояние, то точка пересечения с кривой также смещается на это же расстояние вдоль касательной к кривой.
Теорема о делении отрезков
Любую точку отрезка можно разделить заданным образом с помощью секущей и параллельных ей прямых. Это позволяет строить точки, делящие отрезок в нужном отношении.
Углы, образованные секущей с двумя другими прямыми, обладают замечательным свойством: произведения противолежащих острых углов и тупых углов при пересечении равны.
Это лишь часть интересных фактов о секущих. Дальнейшее изучение теории секущих позволит открыть для себя еще много полезных свойств.
























