Мир цифр и чисел велик и разнообразен. Он полон всевозможных интересных фактов. Без чисел и вычислений уже много веков не обходится ни одно человеческое общество. Известно много выдающихся, талантливых математиков, которые вкладывают всю душу в свои открытия. Именно к таким ученым относился Леонардо Фибоначчи. Молодой математик из маленького городка Пиза внес огромный вклад в науку. Его именем была названа последовательность математических значений "числа Фибоначи". Теперь всем известно, что все в этом мире закономерно и имеет свою последовательность.
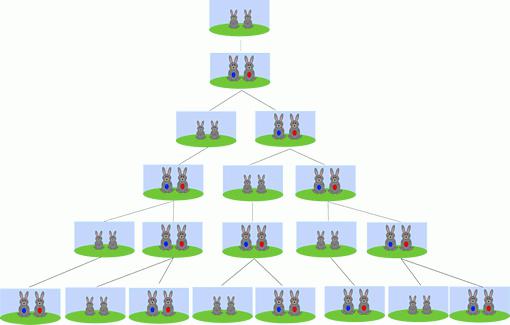
В свое время Леонардо написал «Книгу об абаке», где детально излагал все свои открытия. Так всему миру стала известна задача о кроликах. В ее основе стоят две пары животных, причем одна из них может дать потомство, а вторая - нет. Поэтому в итоге, начиная с третьего поколения, следующее число кроликов будет равно сумме всех членов предыдущих двух. Так была выявлена следующая
последовательность (числа Фибоначи):
1, 1, 2, 3, 5, 8... 610, 987, 1597, 2584... 39088169, 63245986, 102334155
Не менее увлекательным занятием становится и рассмотрение различных спиралей, которые встречаются нам повсюду: ураганы и смерчи, семена в подсолнухах, шишках, листья на деревьях и т.д. Оказывается, что и здесь затаилось число Фибоначи. Если построить спираль и разделить ее на несколько прямоугольников со сторонами 144, 89, 55, то выяснится, что сторона каждой последующей фигуры равна стороне предыдущей. А последовательность этих чисел равна описываемому ряду. А вот если в каждом квадрате провести дуги, то вместе они и образуют спираль. Это в очередной раз доказывает, что
число Фибоначчи просто волшебное.
Однако было выяснено, что с данной последовательностью люди знакомы уже с древних времен. Конечно, можно предположить, что это случайность или простое совпадение. Но факт остается фактом: пирамиды в Гизе построены по принципу числа Фибоначи. Так, площадь каждой грани пирамиды равна ее высоте в квадрате. А если длину ребра разделить на высоту этого удивительного сооружения, то получается число равное 1,618. Именно данная величина получится, если каждое следующее значение из последовательности разделить на предыдущее.
Весомый вклад своим открытием внес Леонардо в экономику. С помощью последовательности чисел сегодня многие экономисты могут спрогнозировать дальнейшую судьбу биржи. Для этого были выявлены уровни Фибоначи. Теперь можно верно определить уровни сопротивления и поддержки или размер коррекции продвижения товара. То есть числа Фибоначи помогают определять, в какую сторону развернется тренд, или рассчитать уровни отката. Продолжение движения первого и тот период, когда закончится последний, также рассчитываются согласно известной последовательности.
Итак, числа Фибоначи можно встретить на каждом шагу. Ведь нас повсюду окружают растения, спирали и интересные здания. Такая последовательность может помочь и в экономике, при контроле и построении развития тренда. Эти числа помогли нам понять, что все в этом мире имеет свою последовательность и закономерность.