Величина рассматривается как одна из основ математики, в частности одного из ее разделов - геометрии. Это понятие уходит глубоко в прошлое. Оно было описано в III веке до н. э. древнегреческим математиком Евклидом в его труде «Начала». Люди применяли величины на протяжении более двух тысяч лет, пока они не подверглись ряду обобщений.
Величина в математике - это очень важная тема для изучения в школе. Фактически из понимания детьми величины строится дальнейшее обучение от простого к все более сложному. Измеряя линейкой различные отрезки и площадь, взвешивая на весах массу, определяя скорость, исходя из расстояния и времени, ребенок постепенно учится постигать материальный мир и строит свою картину восприятия, а также определяет для себя роль математики в окружающем мире.
Понятие величины в математике
Величина в математике - это свойство объектов, которое поддается измерению путем сопоставления с единицей измерения, относящейся к величине этого рода. Выделяют длину, массу, объем, скорость, площадь и время. Говоря простым языком, это то, что можно измерить и выразить числом.

Данный раздел математики ученики проходят еще в начальной школе, и все измерения на этом этапе производятся натуральными числами величины. В математике младших классов такой числовой ряд представляет собой последовательность чисел от 1 и до бесконечности. В старших классах для расчетов величины используются также числа и с отрицательным значением.
Исторический очерк
В древних цивилизациях, в основном в связи с обширным развитием торговли, возникла потребность в измерениях товаров, определении расстояния, времени, расчете посевных площадей и прочего. Сначала люди измеряли предметы при помощи сравнения их с человеком или животным. Но все эти меры были довольно относительными, ведь у каждого свои пропорции тела, а величина в математике - это в первую очередь точность. Поэтому со временем возникла необходимость в создании единого эталона системы величин.
Так, во Франции в 1791 году во время Великой революции единицей измерения длины было принято считать метр, который составлял одну сорокамиллионную часть земного меридиана, пересекающего Париж. Кроме метра была установлена такая величина, как килограмм. Он был равен одному кубическому дециметру воды при температуре 4 °С. А также ар как мера площади, литр и грамм.
Так как в основе новых величин был метр, то и система измерения стала называться метрической. В Национальном архиве Франции до сих пор лежат платиновые эталоны метра в виде линейки со штрихами на концах и килограмма в виде цилиндрической гири.
Русская система измерения
С Древней Руси до принятия в Российской империи метрической системы мер принято было производить замеры с помощью длины локтя, ширины ладони, длины стопы - фут. Расстояние от кончика вытянутой вверх руки до пятки противоположной ноги называлось сажень, расстояние между вытянутыми руками - маховая сажень и т. д. Для измерения расстояния брали, например, слышимость петушиного крика или способность лошади без отдыха добраться из пункта А в пункт Б. Так люди измеряли дальность проложенного маршрута.
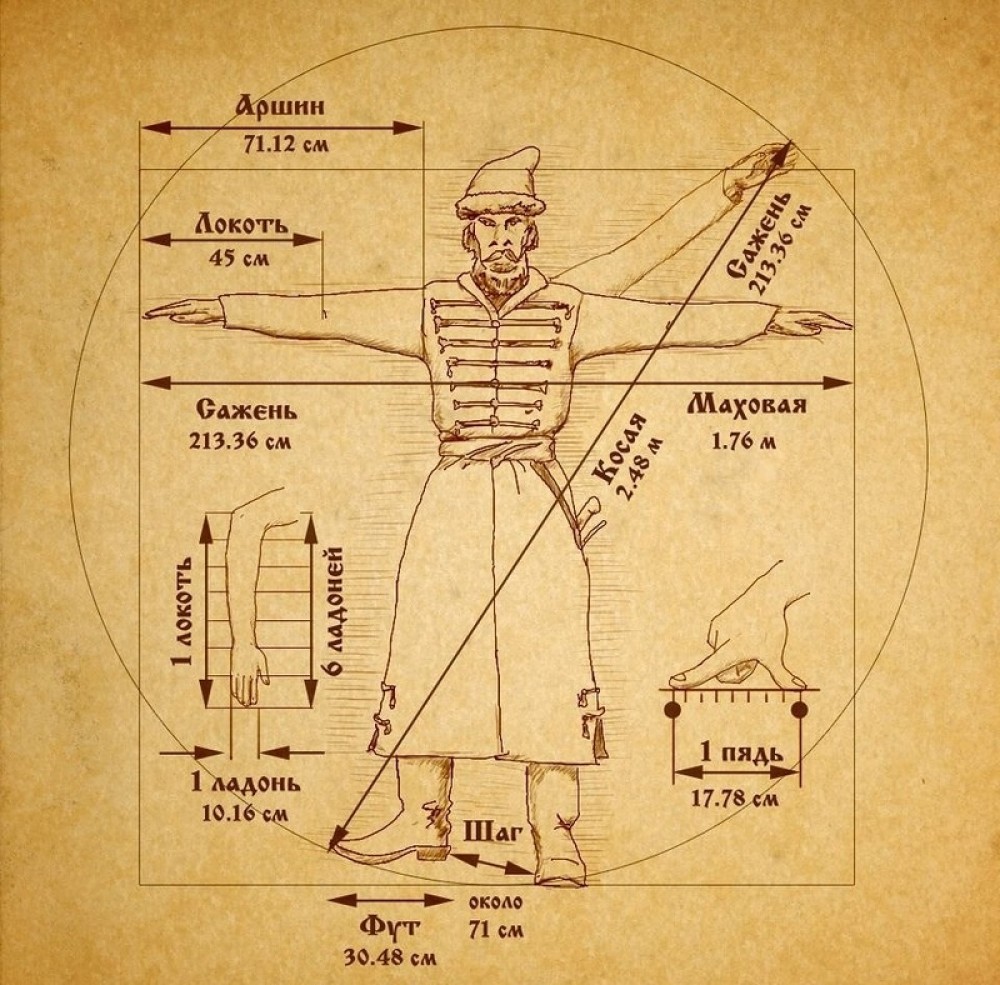
Даже сейчас в пословицах и поговорках мы можем встретить напоминания о существовании старинных величин. Об этом свидетельствую такие выражения, как «слышать за версту», «косая сажень в плечах», «мерить на свой аршин» и другие крылатые фразы.
В 1899 году, 4 июня была принята единая метрическая система, которая являлась необязательной. Обязательной она стала 14 сентября 1918 года уже при советской власти, практически сразу после Великой октябрьской революции.
Основные математические величины
Дети в школе, изучая величины в математике, к 4 классу уже имеют широкое представление о таких значениях, как длина, масса, объем, площадь, скорость и время.
- Под длиной предмета принято понимать характеристику линейного размера. Ее измеряют в миллиметрах, сантиметрах, дециметрах, метрах и километрах. Эту тему в школе дети проходят, начиная с первого класса.

- Масса предмета - еще одна физическая величина, измеряемая в основном граммами и килограммами. А также объем тел, который исчисляется литрами и миллилитрами. Однако не стоит вводить ребенка в заблуждение и считать массу и вес равными понятиями. Масса - это постоянная величина в математике, в то время как вес зависит от силы и скорости притяжения объекта к земле.
- Под площадью геометрической фигуры принято понимать занимаемое ею пространство на плоскости, которое исчисляется в мм2, см2, дм2, м2 и км2.
- Время - понятие довольно относительное и для человека связано с его ощущениями, его нельзя увидеть, но можно почувствовать в смене дня, ночи и времен года. Поэтому для знакомства детей с понятием времени используют точные приборы, такие как песочные часы и часы со стрелкой. Время исчисляется секундами, минутами, часами, днями, годами и так далее.

- На основании пройденной темы о времени и длине дети изучают понятие скорости. По сути, скорость - это отрезок пути, пройденный за некоторое время.
Бесконечная величина измерения в математике
В старших классах школьниками изучается тема бесконечно малых и больших чисел. Это те числовые значения, которые либо стремятся к нулю, либо к бесконечности. Масса дрейфующей льдины в океане, которая находится в процессе таяния, будет относиться к бесконечной малой величине. Ведь под воздействием беспрерывного тепла лед растает, и масса глыбы будет равна нулю. Противоположным процессом с точки зрения физики является расширение Вселенной. Она стремится к бесконечно большой величине, расширяя свои пределы.
Постоянная и переменная величина
В процессе развития математики величины были разделены на два класса: постоянные и переменные.
Постоянная величина, или так называемая научным языком константа, остается неизменной, то есть при любых условиях она сохраняет свое значение. Например, для расчета длины окружности используется постоянная величина «Пи» = 3,14. Константа Пифагора √2=1,41, используемая в математике, также неизменна. Постоянная величина является частным случаем и рассматривается как переменная величина с одинаковым значением.

Переменная величина в математике - это обратный процесс, который по различным причинам меняет свое числовое значение.



























