Прямая и плоскость являются двумя самыми важными геометрическими элементами, с помощью которых можно построить разные фигуры в двумерном и трехмерном пространстве. Рассмотрим, как находить расстояние между параллельными прямыми и параллельными плоскостями.
Математическое задание прямой
Из школьного курса геометрии известно, что в двумерной прямоугольной системе координат прямую можно задать в следующей форме:
y = k*x + b.
Где k и b представляют собой числа (параметры). Записанная форма представления прямой на плоскости является плоскостью, которая параллельна оси z в трехмерном пространстве. Ввиду этого, в данной статье для математического задания прямой воспользуемся более удобной и универсальной формой – векторной.
Предположим, что наша прямая параллельна некоторому вектору u¯(a, b, c) и проходит через точку P(x0, y0, z0). В таком случае в векторной форме ее уравнение будет представлено следующим образом:
(x, y, z) = (x0, y0, z0) + λ*(a, b, c).
Здесь λ – это любое число. Если явно представить координаты, раскрыв записанное выражение, то мы получим параметрическую форму записи прямой.
С векторным уравнением удобно работать при решении различных задач, в которых необходимо определить расстояние между прямыми параллельными.
Прямые и расстояние между ними
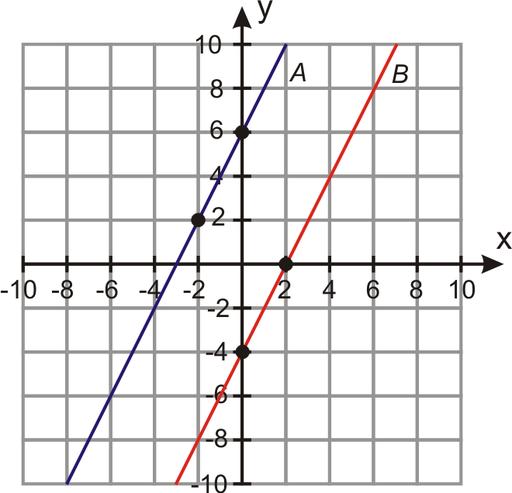
Говорить о расстоянии между прямыми имеет смысл только тогда, когда они являются параллельными (в трехмерном случае также существует ненулевое расстояние между прямыми скрещивающимися). Если прямые пересекаются, то очевидно, что они находятся на нулевом расстоянии друг от друга.
Расстоянием между прямыми параллельными называется длина соединяющего их перпендикуляра. Чтобы определить этот показатель, достаточно выбрать произвольную точку на одной из прямых и из нее опустить перпендикуляр на другую.
Опишем кратко процедуру нахождения искомой дистанции. Предположим, что нам известны векторные уравнения двух прямых, которые представлены в следующем общем виде:
(x, y, z) = P + λ*u¯;
(x, y, z) = Q + β*v¯.
Построим параллелограмм на этих прямых так, что одной из сторон будет PQ, а второй, например, u. Очевидно, что высота данной фигуры, проведенная из точки P, является длиной искомого перпендикуляра. Для ее нахождения можно применить следующую простую формулу:
d = |[PQ¯*u¯]|/|u¯|.
Поскольку расстоянием между прямыми параллельными называется длина перпендикулярного отрезка между ними, то согласно записанному выражению достаточно найти модуль векторного произведения PQ¯ и u¯ и разделить полученный результат на длину вектора u¯.
Пример задачи на определение между прямыми расстояния
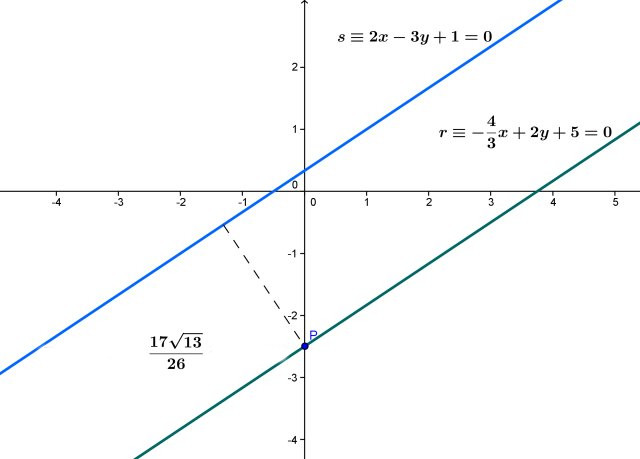
Заданы две прямые следующими векторными уравнениями:
(x, y, z) = (2, 3, -1) + λ*(-2, 1, 3);
(x, y, z) = (1, 1, 1) + β*(2, -1, -3).
Из записанных выражений видно, что мы имеем две параллельные прямые. Действительно, если умножить на -1 координаты направляющего вектора первой прямой, то получатся координаты направляющего вектора второй прямой, что говорит об их параллельности.
Расстояние между прямыми параллельными вычислим, используя записанную в предыдущем пункте статьи формулу. Имеем:
P(2, 3, -1), Q(1, 1, 1) => PQ¯ = (-1, -2, 2);
u¯ = (-2, 1, 3).
Тогда получаем:
|u¯| = √14 см;
d = |[PQ¯*u¯]|/|u¯| = √(90/14) = 2,535 см.
Отметим, что вместо точек P и Q для решения задачи можно было использовать абсолютно любые точки, которые принадлежат данным прямым. При этом мы получили бы то же самое расстояние d.
Задание плоскости в геометрии
Выше был рассмотрен подробно вопрос о расстоянии между прямыми. Теперь покажем, как находить расстояние между параллельными плоскостями.
Каждый представляет, что такое плоскость. Согласно математическому определению, указанный геометрический элемент представляет собой совокупность точек. Причем если составить всевозможные вектора с помощью этих точек, то все они будут перпендикулярны одному единственному вектору. Последний принято называть нормалью к плоскости.
Для задания уравнения плоскости в трехмерном пространстве чаще всего пользуются общей формой уравнения. Она имеет такой вид:
A*x + B*y + C*z + D = 0.
Где большие латинские буквы – это некоторые числа. Удобно пользоваться этим видом уравнения плоскости потому, что в нем явно заданы координаты нормального вектора. Они равны A, B, C.
Нетрудно понять, что две плоскости являются параллельными только тогда, когда их нормали параллельны.
Как найти расстояние между двумя параллельными плоскостями ?
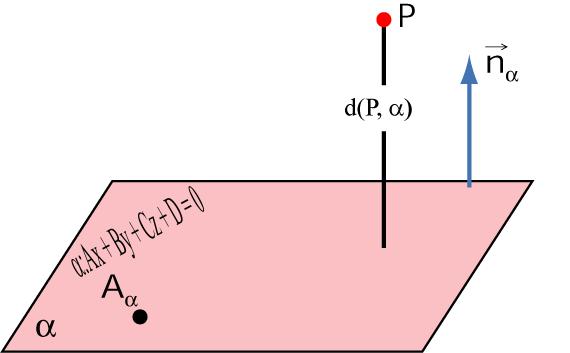
Чтобы определить указанное расстояние, следует четко представлять, о чем идет речь. Под расстоянием между плоскостями, которые друг другу параллельны, понимают длину перпендикулярного им отрезка. Концы этого отрезка принадлежат плоскостям.
Алгоритм решения подобных задач прост. Для этого найти необходимо координаты абсолютно любой точки, которая принадлежит одной из двух плоскостей. Затем, следует воспользоваться такой формулой:
d = |A*x0 + B*y0 + C*z0 + D|/√(A2 + B2 + C2).
Поскольку расстояние – это величина положительная, то в числителе стоит знак модуля. Записанная формула является универсальной, поскольку она позволяет рассчитать дистанцию от плоскости до абсолютно любого геометрического элемента. Достаточно лишь знать координаты одной точки этого элемента.
Для полноты информации отметим, что если нормали двух плоскостей друг другу не параллельны, то такие плоскости будут пересекаться. Дистанция между ними тогда будет равна нулю.
Задача на определение дистанции между плоскостями
Известно, что две плоскости заданы следующими выражениями:
y/5 + x/(-3) + z/1 = 1;
-x + 3/5*y + 3*z – 2 = 0.
Необходимо доказать, что плоскости являются параллельными, а также определить дистанцию между ними.
Чтобы ответить на первую часть задачи, необходимо первое уравнение привести к общей форме. Отметим, что оно дано в так называемом виде уравнения в отрезках. Умножим его левую и правую части на 15 и перенесем все члены в одну сторону равенства, получим:
-5*x + 3*y + 15*z – 15 = 0.
Выпишем координаты двух нормальных векторов плоскостей:
n1¯ = (-5, 3, 15);
n2¯ = (-1, 3/5, 3).
Видно, что если n2¯ умножить на 5, то мы точно получим координаты n1¯. Таким образом, рассматриваемые плоскости являются параллельными.
Чтобы вычислить расстояние между параллельными плоскостями, выберем произвольную точку первой из них и воспользуемся приведенной ранее формулой. Например, возьмем точку (0, 0, 1), которая принадлежит первой плоскости. Тогда получаем:
d = |A*x0 + B*y0 + C*z0 + D|/√(A2 + B2 + C2) =
= 1/(√(1 + 9/25 + 9 )) = 0,31 см.
Искомое расстояние составляет 31 мм.
Дистанция между плоскостью и прямой
Предоставленные теоретические знания позволяют также решить задачу на определение расстояния между прямой и плоскостью. Выше уже упоминалось, что формула, справедливая для расчетов между плоскостями, является универсальной. Ею также можно воспользоваться для решения поставленной задачи. Для этого достаточно выбрать любую точку, которая принадлежит заданной прямой.
Главной проблемой при определении расстояния между рассматриваемыми геометрическими элементами является доказательство их параллельности (если это не так, то d=0). Параллельность легко доказать, если вычислить скалярное произведение нормали и направляющего вектора для прямой. Если рассматриваемые элементы параллельны, то это произведение будет равно нулю.


























