Закон Био-Савара-Лапласа - фундаментальный физический закон, устанавливающий связь между электрическим током и создаваемым им магнитным полем. Этот закон позволяет рассчитывать характеристики магнитного поля для проводников произвольной конфигурации.
1. Предпосылки открытия закона Био-Савара
В 1820 году датский ученый Ханс Христиан Эрстед экспериментально обнаружил, что электрический ток влияет на магнитную стрелку. Это фундаментальное открытие показало, что существует какая-то связь между электричеством и магнетизмом, которые до этого считались совершенно разными явлениями.
Открытие Эрстеда послужило толчком для дальнейших исследований в этом направлении. В частности, французский ученый Андре-Мари Ампер начал изучать силовое взаимодействие между проводниками с током. Он сформулировал количественный закон Ампера, математически описывающий это взаимодействие.
Однако Ампер рассматривал в основном простейший случай - взаимодействие прямолинейных проводников с током. Требовалось более общее описание связи электрического тока в проводнике и создаваемого этим током магнитного поля в окружающем пространстве. Эту задачу взяли на себя французские ученые Жан Батист Био и Феликс Савар.
2. Формулировка закона Био-Савара
Жан Батист Био был известным французским физиком, профессором Сорбонны и членом Французской академии наук. Феликс Савар также был физиком, специалистом в области акустики. Узнав об открытии Эрстеда, Био и Савар начали серию экспериментов по исследованию магнитных полей, создаваемых электрическими токами в проводниках различной конфигурации.

В ходе экспериментов Био и Савар выявили важные закономерности. Во-первых, они ввели понятие элементарного участка тока - очень малого прямолинейного отрезка проводника Δl, по которому течет ток силой I. Хотя такой участок теоретически нельзя реально выделить в замкнутой электрической цепи, но с математической точки зрения с ним удобно работать.
Во-вторых, Био и Савар сформулировали важный принцип суперпозиции: магнитное поле от всего проводника можно представить как векторную сумму магнитных полей, создаваемых всеми элементарными участками тока в отдельности.
На основании многочисленных измерений Био и Савар получили формулу, связывающую характеристики элементарного участка тока Δl и создаваемой им напряженности магнитного поля ΔH в некоторой точке пространства:
ΔH = (1/(4π)) · I · Δl · sinθ / r2
Здесь I - сила тока в элементе Δl, r - расстояние от элемента до рассматриваемой точки, θ - угол между направлением элемента и направлением на точку. Таким образом, с помощью этой формулы по заданному распределению токов можно рассчитать магнитное поле в любой точке пространства.
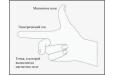
Для определения направления вектора магнитного поля ΔH Био и Савар предложили использовать так называемое правило правой руки . Согласно этому правилу, если указательный палец правой руки направлен по направлению тока I в элементе Δl, а средний палец - по направлению от элемента Δl к точке наблюдения, то отставленный в сторону большой палец укажет направление вектора магнитной индукции ΔH в этой точке.

3. Обобщение закона Био-Савара Лапласом
Хотя закон Био-Савара позволял рассчитать магнитное поле для относительно простых конфигураций тока, он не мог быть напрямую применен для сложных, произвольно изогнутых проводников.
Для решения этой проблемы потребовалось обобщение закона Био-Савара на сложные контуры с током. Такое обобщение предложил выдающийся французский математик и физик Пьер-Симон Лаплас.
Лаплас исходил из того, что любой, даже самый сложный проводник можно мысленно разбить на большое число элементарных участков Δl. Для каждого такого участка можно использовать закон Био-Савара и рассчитать его вклад в магнитное поле в данной точке пространства.
А поскольку, согласно принципу суперпозиции, результирующее магнитное поле является векторной суммой полей от всех элементарных участков, то, просуммировав эти вклады, можно получить поле от сложного проводника.
4. Теорема о циркуляции магнитной индукции
Для выполнения такого суммирования Лаплас использовал математический аппарат дифференциального и интегрального исчисления. В частности, он сформулировал теорему о циркуляции вектора магнитной индукции.
Эта теорема позволяет значительно упростить расчеты в тех случаях, когда проводник с током обладает некоторой симметрией. Тогда вместо интегрирования по всем элементарным участкам достаточно воспользоваться интегралом по замкнутому контуру.
5. Связь закона Био-Савара и уравнений Максвелла
В дальнейшем закон Био-Савара послужил одной из основ для формулировки уравнений Максвелла, полностью описывающих электромагнитное поле и его связь с электрическими зарядами и токами.
При определенных допущениях (в частности, при постоянстве электрического поля) уравнения Максвелла могут быть преобразованы математически и приведены именно к закону Био-Савара.
Таким образом, с формальной точки зрения закон Био-Савара является частным решением уравнений Максвелла для случая магнитостатического поля (не зависящего от времени).
6. Применение закона Био-Савара на практике
Несмотря на последующее развитие теории электромагнетизма, закон Био-Савара до сих пор остается востребованным с практической точки зрения.
Во-первых, его используют при расчете магнитных полей в электрических машинах, двигателях, трансформаторах и других технических устройствах. Эти расчеты важны для оптимального проектирования таких устройств.
Во-вторых, на основе закона Био-Савара оценивают уровень магнитных полей, создаваемых линиями электропередач, электрическими приборами и другими источниками. Это необходимо для изучения возможного влияния этих полей на здоровье человека.
7. Примеры использования закона Био-Савара
Рассмотрим несколько конкретных примеров применения закона Био-Савара для расчета магнитных полей.
7.1. Магнитное поле прямого провода с током
Как уже упоминалось ранее, для прямолинейного участка провода с током I формула Био-Савара имеет простой вид:
H = (1/(4π)) · I · l / r2
Эту формулу часто используют, например, при расчете магнитных полей вблизи линий электропередач.
7.2. Магнитное поле катушки с током
Если согнуть провод с током в виде витков катушки, то для расчета магнитного поля внутри такой катушки также можно воспользоваться законом Био-Савара и принципом суперпозиции.
При этом нужно будет выполнить интегрирование вкладов от всех витков, что в общем случае довольно сложно. Но для идеальной катушки (с бесконечным числом витков) решение получается достаточно простым.
8. Электромагнетизм и закон Био-Савара
Как уже отмечалось ранее, закон Био-Савара установил глубокую взаимосвязь между электричеством и магнетизмом - двумя явлениями, которые до 19 века считались практически не связанными.
Согласно современным представлениям, электрическое и магнитное поля являются проявлениями единого электромагнитного поля. И закон Био-Савара можно рассматривать как первый количественный результат, указывающий на эту глубинную взаимосвязь.
9. Значение закона Био-Савара
Подводя итог, еще раз отметим огромное значение закона Био-Савара для развития науки об электромагнетизме и его многочисленные практические приложения.
По сути, этот закон положил начало инженерным расчетам магнитных полей электрических цепей и устройств, что и сейчас имеет большое значение во многих областях науки и техники.