Знаете ли вы, что на самом деле представляет собой функция в математике и зачем нужно знать ее область значения? Эта информация пригодится для решения многих прикладных задач. Давайте разберемся!

Основные определения
Функция в математике - это зависимость одной переменной от другой. Переменная, от которой что-то зависит, называется независимой переменной или аргументом функции и обозначается чаще всего буквой x. Переменная, которая зависит, называется зависимой переменной или значением функции и обозначается буквой y.
Например, в функции y = 3x + 5 независимая переменная x может принимать любые значения, а значение y будет зависеть от того, какое значение мы подставим вместо x.
Например, для функции y = x2 область определения - все действительные числа. Подставляя любые действительные числа вместо x, мы получаем неотрицательные значения y. Значит, область значений этой функции - множество всех неотрицательных действительных чисел.
Область значений функции y = f(x) принято обозначать E(f).
Методы нахождения области значений
Существует два основных метода нахождения области значений функции:
- Графический метод
- Аналитический метод
При графическом методе строится график функции, а затем по графику определяется наибольшее и наименьшее значение, которое принимает функция. Это дает нам числовой промежуток - область значений.
Аналитический метод заключается в исследовании самой формулы функции. Находятся точки максимума и минимума, вычисляются пределы функции, а затем определяется область значений исходя из полученных данных.
Подробнее рассмотрим алгоритм аналитического метода. Если функция непрерывна на некотором отрезке [a; b], то:
- Находим производную функции
- Находим точки максимума и минимума функции на данном отрезке
- Определяем наибольшее и наименьшее значение функции на отрезке
- Записываем область значений в виде числового отрезка [ymin; ymax]
Если функция задана на интервале (a; b) или имеет точки разрыва, алгоритм аналогичный, но в нем используются пределы функции.
Давайте теперь разберем конкретные примеры пошагового нахождения области значения различных функций.
Пошаговые алгоритмы с примерами
Давайте разберем конкретные примеры пошагового нахождения области значения различных функций.

Пример 1. Линейная функция
Найдем область значения линейной функции вида y = 2x + 1 на отрезке [-3; 5]:
- Производная функции равна 2 и не зависит от x
- Так как производная положительна на всем отрезке, то функция возрастает и не имеет экстремумов
- Подставляем границы отрезка в функцию:
- При x = -3, y = 2*(-3) + 1 = -5 При x = 5, y = 2*5 + 1 = 11
- Получаем, что область значения функции на отрезке [-3; 5] есть отрезок [-5; 11]
Пример 2. Квадратичная функция
Найдем область значения квадратичной функции вида y = x2 - 4x + 5 на интервале (-∞; 2):
- Производная функции равна 2x - 4
- Приравниваем производную к 0 и получаем точку экстремума x = 2
- В этой точке функция принимает значение y = 4 - 8 + 5 = 1
- Когда x стремится к -∞, то y стремится к +∞
- Когда x = 2, y = 1
- Получаем область значения в виде интервала (1; +∞)
Пошаговый алгоритм нахождения области значения функции
Как мы уже выяснили ранее, что такое область значения функции - это множество всех значений зависимой переменной y, которые функция может принимать при подстановке значений независимой переменной x из ее области определения.
Давайте еще раз вспомним общий алгоритм нахождения области значения функции аналитическим методом:
- Находим производную функции
- Исследуем функцию на экстремумы
- Находим пределы функции на границах области определения
- Объединяем полученные данные и записываем область значений
Рассмотрим применение этого алгоритма для функции y = tg(x).
Изучение свойств функции y=tgx начнем с построения графика. Обратимся к единичной окружности:
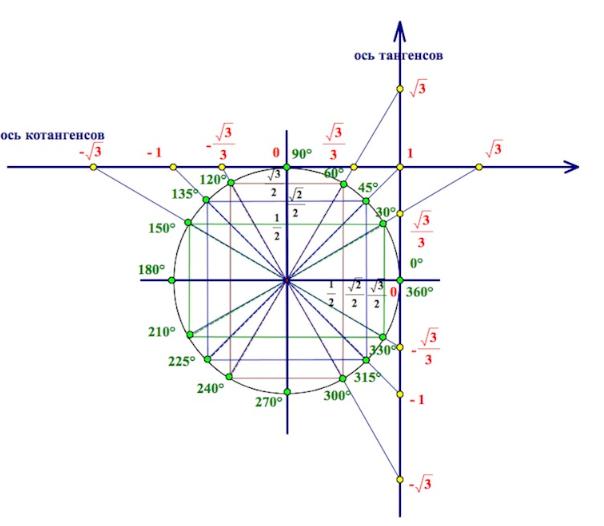
Вычислите:
1.
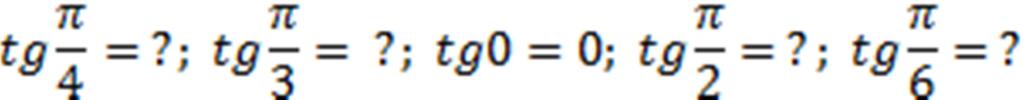
Ответ:
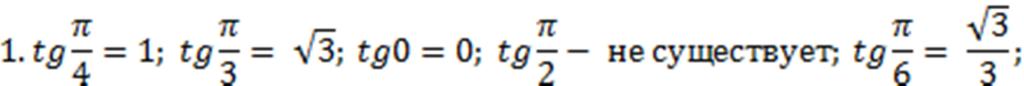
Заключение
Мы рассмотрели основные определения, связанные с понятием области значений функции, изучили методы ее нахождения и разобрали конкретные примеры.
Надеюсь, эта информация поможет вам легко справляться с заданиями на нахождение областей значений различных функций на практике. Успехов!



























