Загадочная высота треугольника хранит множество тайн. Давайте отправимся в увлекательное путешествие, чтобы открыть для себя потрясающие факты о самой короткой, самой длинной и скрытой высотах.
I. Определение и виды высоты треугольника
Формально, высота треугольника — это перпендикуляр, опущенный из вершины фигуры на противоположную сторону. В зависимости от вида треугольника, высота может иметь разное расположение.
В остроугольном треугольнике все три высоты целиком лежат внутри фигуры. Они пересекаются в одной точке, которая называется ортоцентром.
В прямоугольном треугольнике высота, проведенная к гипотенузе, совпадает с одним из катетов. Ортоцентр находится в вершине прямого угла.
В тупоугольном треугольнике одна высота целиком лежит внутри фигуры. Две другие высоты выходят за пределы треугольника, а их пересечение (ортоцентр) находится вне плоскости треугольника.
II. Удивительные свойства высоты треугольника
Свойства высоты в треугольнике действительно удивительны. Давайте рассмотрим некоторые из них.
1. Три высоты пересекаются в одной точке - ортоцентре
Это фундаментальное свойство высоты справедливо для любого треугольника. Ортоцентр всегда является общей точкой пересечения трех высот или их продолжений.
Для остроугольного треугольника это свойство доказывается с помощью построения параллельных прямых. Получается, что высоты являются серединными перпендикулярами к сторонам некоторого вспомогательного треугольника, а такие перпендикуляры всегда пересекаются в одной точке.
В прямоугольном треугольнике, как мы уже отметили, ортоцентр совпадает с вершиной прямого угла. А для тупоугольного треугольника приходится рассматривать продолжения высот.
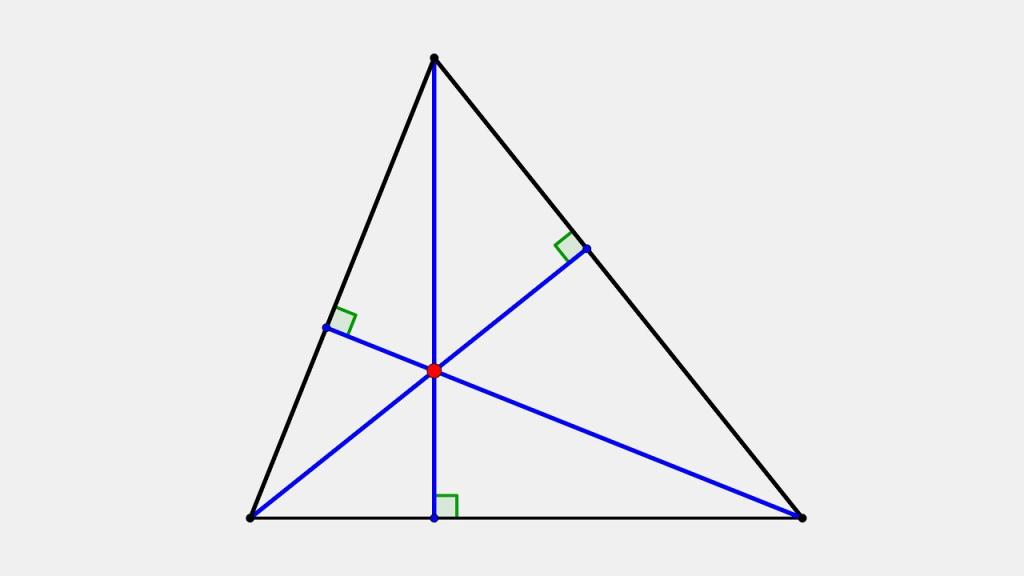
2. Ортоцентр и описанная окружность
Существует интересное свойство симметрии ортоцентра треугольника относительно сторон:
Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.
Это позволяет строить описанную окружность, зная положение ортоцентра и используя циркуль и линейку. Также по этому свойству можно решать различные геометрические задачи.
Например, если известны координаты вершин треугольника и его ортоцентра, то можно найти радиус и центр описанной окружности.
3. Высоты и площадь треугольника
Существует интересная закономерность между высотами треугольника и его сторонами:
- Высоты треугольника обратно пропорциональны соответствующим сторонам
Это означает, что произведение высоты на длину противоположной стороны постоянно для данного треугольника. Благодаря этому свойству по известным высотам можно вычислить площадь треугольника по формуле:
S = (ah)1(bh)2(ch)3 / 4R, где R - радиус описанной окружности.
4. Удивительное равенство пред- и поствысот
В любом треугольнике справедливо неожиданное равенство:
Сумма квадратов двух предвысот равна сумме квадратов двух поствысот.
Под предвысотой понимается расстояние от вершины треугольника до основания высоты, проведенной из этой вершины. А поствысота - расстояние от конца высоты до середины противоположной стороны.
Это удивительное свойство выполняется даже для тупоугольного треугольника, несмотря на то, что не все высоты лежат внутри него!
5. Построение ортотреугольника
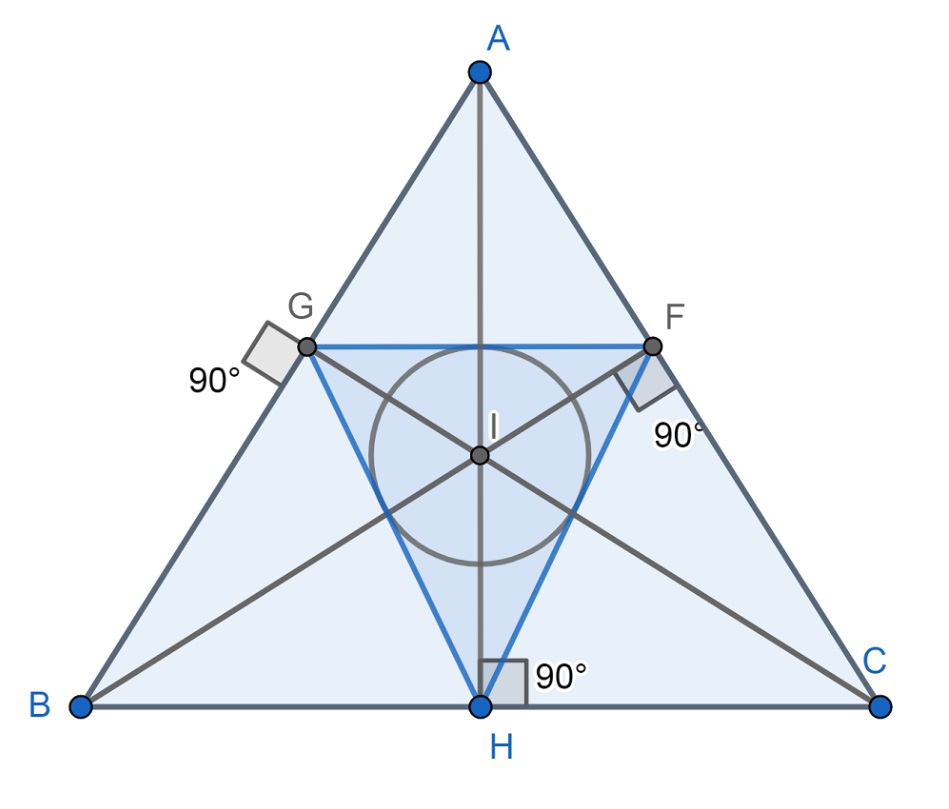
Через основания высот исходного треугольника можно построить особый ортотреугольник. У него есть интересные свойства.
В частности, для остроугольного треугольника центр окружности, вписанной в ортотреугольник, совпадает с точкой пересечения высот - ортоцентром.
6. Удивительные свойства ортоцентра
Сама точка пересечения высот - ортоцентр - тоже обладает любопытными особенностями.
Так, ортоцентр может лежать как внутри самого треугольника (для остроугольного), так и вне его (для тупоугольного). А в некоторых случаях ортоцентр совпадает с одной из замечательных точек треугольника.
Например, для равностороннего треугольника ортоцентр, центр описанной окружности и центр вписанной окружности находятся в одной точке!
7. Практическое применение ортоцентра
Знание свойств ортоцентра позволяет решать разнообразные геометрические задачи.
Например, если известно расположение ортоцентра и двух вершин треугольника, можно вычислить его третью вершину или углы при известных вершинах.
8. Высота треугольника в архитектуре и строительстве
Высота треугольника широко используется в архитектуре и строительстве благодаря важному свойству:
- Чем выше высота треугольника, тем устойчивее конструкция
Поэтому при проектировании различных сооружений - мостов, башен, крыш - конструкторы стремятся максимизировать высоту треугольников в их основе для повышения прочности.
9. Применение в оптике
Благодаря отражательным свойствам, высота треугольника используется при построении оптических систем.
Например, высота в треугольнике, образованном лучом, падающим на зеркало, позволяет определить положение отраженного луча и построить изображение в зеркале.
10. Использование симметрии в дизайне
Интересные эффекты дает использование свойств высоты и ортоцентра треугольника при создании различных узоров и орнаментов.
Симметрия относительно высот или ортоцентра порождает удивительные фрактальные структуры, которые применяются в прикладном искусстве и дизайне.























