Гипербола - одна из важнейших кривых в математике, которая широко применяется в науке, технике и искусстве. В этой статье мы подробно разберем, как построить гиперболу вручную и с помощью компьютерных программ.
Теория гиперболы
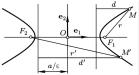
Гипербола - это множество точек на плоскости, у которых абсолютная величина разности расстояний до двух фиксированных точек (фокусов) постоянна. Формально гипербола определяется уравнением:
x2/a2 - y2/b2 = 1
Здесь a и b - положительные числа, называемые полуосями гиперболы. Это каноническое уравнение гиперболы.
Основные элементы гиперболы:
- Вершины - точки пересечения гиперболы с ее осями.
- Асимптоты - прямые, к которым бесконечно приближаются ветви гиперболы.
- Фокусы - две точки, от которых отсчитываются расстояния.
- Директрисы - прямые, от которых расстояния пропорциональны.
По соотношению полуосей различают равносторонние (a = b) и неравносторонние (a ≠ b) гиперболы. Важной характеристикой является эксцентриситет e = √(a2 + b2)/a, показывающий "растянутость" гиперболы.
Гипербола симметрична относительно осей координат. У нее есть два важных свойства:
- Асимптотическое: с ростом x и y гипербола неограниченно приближается к своим асимптотам.
- Фокальное: абсолютная величина разности расстояний любой точки гиперболы до фокусов постоянна и равна 2a.
Теперь, когда мы разобрали основные теоретические сведения о гиперболе, можно перейти к практике ее построения.
Построение гиперболы вручную
Существует определенный алгоритм построения гиперболы по ее каноническому уравнению:
- Находим координаты вершин и уравнения асимптот.
- Выбираем точки и находим их координаты для отображения гиперболы.
- Рисуем четверть гиперболы.
- Отражаем ее относительно осей координат.
Рассмотрим построение равносторонней гиперболы, у которой a = b:
x2/9 - y2/9 = 1
Вершины имеют координаты (3; 0) и (-3; 0). Асимптоты совпадают с осями координат. Выберем точки (2; 1), (1; 2) и построим соответствующую четверть. Затем отразим ее относительно осей и получим готовую гиперболу:
Аналогично можно построить неравностороннюю гиперболу. Например, для уравнения:
x2/16 - y2/9 = 1
получим такой график:
Построение гиперболы имеет некоторые особенности в различных четвертях координатной плоскости, которые нужно учитывать. Кроме того, возможно построение по уравнению общего вида с использованием преобразований.
В целом процесс построения гиперболы вручную довольно прост, главное - выбрать удобный масштаб, чтобы изображение получилось аккуратным и понятным.
Построение гиперболы в программах
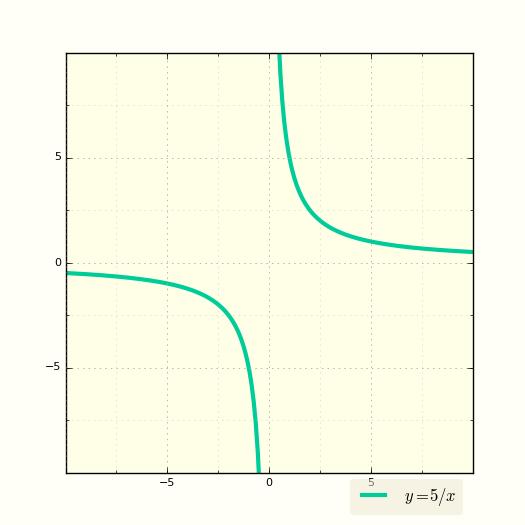
Помимо ручного построения, гиперболу можно изобразить с помощью различных компьютерных программ и графических пакетов.
Одним из простых вариантов является использование графических калькуляторов, например Casio fx-CG50. В них достаточно ввести уравнение гиперболы в поле функций и настроить диапазон отображения осей координат.
Более мощным инструментом служат математические пакеты, такие как GeoGebra, Maple, Mathematica. Они позволяют не только строить гиперболу, но и демонстрировать анимацию ее изменения при варьировании коэффициентов.
Полученное изображение гиперболы можно экспортировать в растровом или векторном формате и использовать в документах и презентациях.
Построение гиперболы в CAD-системах
Для инженерных и архитектурных задач гиперболу часто строят в специализированных CAD-системах.
В КОМПАС-3D гиперболу можно построить с помощью команды "Кривая по описанию" и задания параметрических уравнений. В AutoCAD используется команда "Гипербола" с указанием осей и эксцентриситета.
В SolidWorks для создания гиперболической поверхности применяют команду "Сдвиг" к основанию с криволинейным профилем. Параметры сдвига задают форму гиперболы.
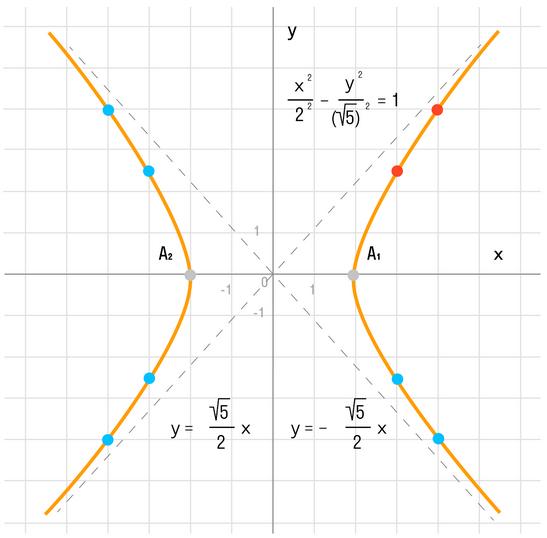
Сравнение методов построения гиперболы
Разные способы построения гиперболы имеют свои преимущества и недостатки:
- Ручное построение просто, но требует аккуратности.
- Графические калькуляторы удобны для быстрого просмотра.
- Математические пакеты дают точный результат, но требуют знания формул.
- CAD-системы нужны для создания чертежей и 3D-моделей.
Таким образом, метод следует выбирать исходя из конкретных задач и имеющихся навыков пользователя.
Применение гиперболы на практике
Гипербола широко используется благодаря своим уникальным математическим свойствам. Рассмотрим некоторые примеры.
В физике гипербола описывает движение тела в поле тяготения при начальной скорости, превышающей вторую космическую. Траектории космических аппаратов при полетах к другим планетам часто имеют гиперболическую форму.
В архитектуре и строительстве гиперболические конструкции обладают высокой прочностью при низком весе. Известные примеры - купола церквей гениального архитектора Антонио Гауди.
В радиотехнике форма гиперболоида используется для создания направленных свойств антенн. Гиперболические антенны применяются в спутниковой связи.
В оптике гиперболические линзы обладают способностью фокусировать параллельные лучи в одной точке, что используется в осветительных приборах.