Круги Эйлера представляют собой удобный графический метод для решения различных текстовых задач. С помощью пересечений и объединений множеств, изображенных в виде кругов, можно проиллюстрировать условие задачи и наглядно найти решение.
В данной статье приводятся примеры использования диаграмм Венна или кругов Эйлера для решения математических задач. Рассматриваются задачи на определение количества элементов в пересечениях и объединениях множеств.
Круги Эйлера позволяют решать задачи различной сложности - от простейших до олимпиадных. Этот метод подходит как для самостоятельного изучения, так и для использования на уроках математики или занятиях математических кружков.
Простейший пример решения задачи с помощью кругов Эйлера
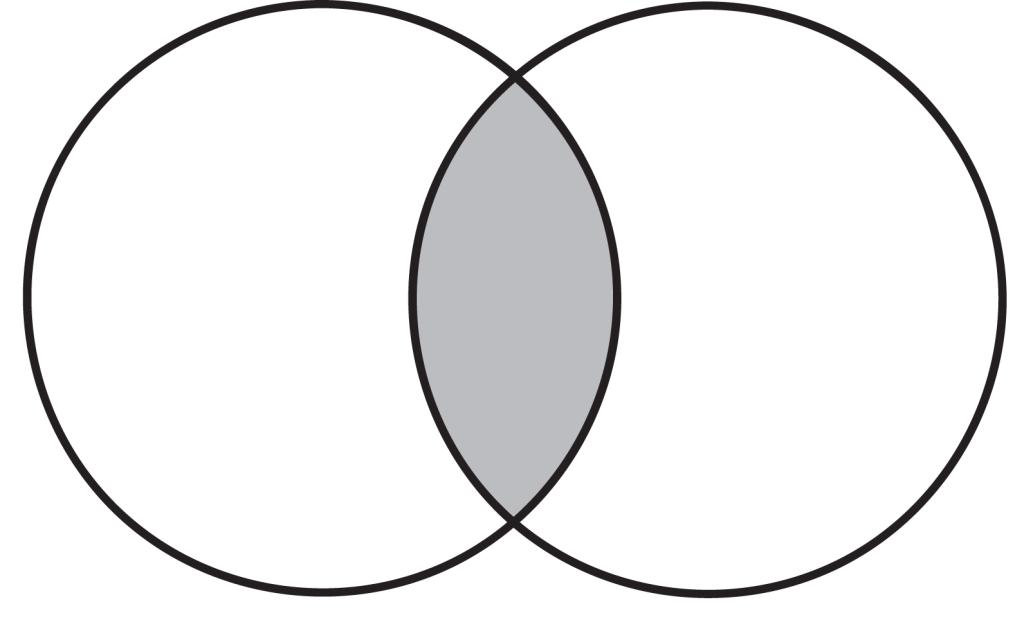
Одним из простейших примеров использования кругов Эйлера является задача о выборе школьниками фильмов для просмотра. Допустим, 15 учеников посмотрели фильм «Обитаемый остров», 11 - «Стиляги», причем 6 школьников посмотрели оба фильма. Требуется определить, сколько детей смотрели только «Стиляги».
Решение с помощью диаграммы выглядит следующим образом: отображаем два множества - тех, кто смотрел «Обитаемый остров» и «Стиляги». В области пересечения указываем 6 человек, которые смотрели оба фильма. Затем подсчитываем: всего «Стиляги» посмотрели 11 школьников, из которых 6 также смотрели «Обитаемый остров». Следовательно, только «Стиляги» посмотрели 11 - 6 = 5 человек.
Таким образом, используя графический метод диаграмм Эйлера, мы легко находим ответ на поставленный вопрос. Круги позволяют наглядно представить данные и увидеть логику решения, не прибегая к громоздким математическим выкладкам.
Использование кругов Эйлера для решения задач повышенной сложности
Круги Эйлера - эффективный инструмент для решения не только простых, но и более сложных логических и комбинаторных задач. Рассмотрим несколько примеров.
Допустим, в классе 35 учеников, 25 из которых берут книги в школьной библиотеке, а 20 - в районной. Требуется определить, сколько детей посещают только школьную библиотеку, только районную и обе библиотеки.
Чертим два круга Эйлера для обозначения школьной и районной библиотек. Обозначаем пересечение двух множеств - это те 10 учеников, которые пользуются услугами обеих библиотек одновременно. Затем находим количество посетителей только школьной библиотеки - вычитаем из 25 читателей школьной библиотеки 10 пересекающихся с районной. Получаем 15 человек. Аналогично для районной библиотеки - 20 минус 10, то есть 10 учеников.
Еще один пример - задача про чтение книг о заклинаниях Гарри Поттером, Роном и Гермионой. Известно общее количество книг и сколько их прочитал каждый персонаж, а также наличие пересечений. Требуется найти, сколько книг прочитал только Рон.
Решение выглядит следующим образом: обозначаем три круга для каждого персонажа и указываем все известные данные на диаграмме - количество прочитанных книг и книг в общих пересечениях. После визуализации условий задачи ответ легко находится подсчетом оставшихся книг в круге Рона.
Применение метода на олимпиадах и математических соревнованиях
Круги Эйлера - довольно распространенный инструмент при решении заданий на математических олимпиадах или других интеллектуальных состязаниях по математике. Это связано с тем, что данный графический метод позволяет оперативно производить логические операции над множествами и находить необходимые характеристики.
Рассмотрим типичный пример задачи с олимпиады, которую эффективно можно решить с помощью диаграмм Венна. В условии говорится, что в трех 7 классах учатся 70 детей. 27 из них занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. Также известны данные о количестве пересечений этих множеств учеников.
Чертим три круга для обозначения занятий и отмечаем все числовые данные на диаграмме. После визуализации условий легко находятся ответы на вопросы задачи путем простого подсчета или вычитания. К примеру, число детей, которые ни в чем из перечисленного не участвуют, находится как разность между общим количеством и суммой всех остальных групп.
Такой подход с использованием графического представления данных позволяет избежать громоздких логических построений и быстро найти решение даже для довольно запутанных на первый взгляд задач.
Особенности графического метода для различных типов задач
Круги Эйлера универсальны и могут использоваться для решения самых разных типов логических, вероятностных, комбинаторных и других математических задач. Рассмотрим некоторые особенности применения этого графического метода.
Для задач на перебор вариантов и подсчет числа объектов, удовлетворяющих заданным условиям, круги Эйлера позволяют наглядно разделить множество на непересекающиеся подмножества. Например, если требуется подсчитать число спортсменов, играющих в футбол и теннис, мы рисуем два непересекающихся круга и находим ответ сложением соответствующих областей диаграммы.
Для задач на вычисление вероятностей круги Эйлера используются для визуализации событий и установления логических отношений включения/исключения между ними, что в дальнейшем помогает применить нужные формулы.
В задачах на доказательство каких-либо утверждений применение кругов Эйлера зачастую позволяет обнаружить логические нестыковки в условии или выявить скрытые зависимости между данными. Это может подсказать верное направление для построения строгого доказательства.
Таким образом, графический метод кругов Эйлера обладает высокой универсальностью и применим для решения широкого спектра математических заданий. Правильное использование данного инструмента требует понимания особенностей конкретного типа задачи.
Ключи и подсказки для использования диаграмм Венна
Эффективное использование кругов Эйлера в решении задач требует выработки определенных навыков и знания некоторых полезных приемов. Давайте рассмотрим ключи к успеху применения этого графического метода.
Во-первых, нужно четко представлять, как именно будут использоваться круги еще до того, как вы начнете их рисовать. Проанализируйте условие задачи, выделите ключевые объекты, которые будут представлены кругами, и логические связи между ними.
Во-вторых, при создании диаграммы Венна обязательно подпишите каждый круг, указав, что именно он обозначает. Также подпишите области пересечений кругов, если они присутствуют в условии задачи. Это позволит избежать путаницы.
В-третьих, аккуратно нанесите на диаграмму все числовые и логические данные, упомянутые в тексте задачи. Используйте для этого подписи, стрелки, различия в штриховке и так далее.
В-четвертых, используйте круги Эйлера не только для поиска решения, но и для проверки найденного ответа. Подставьте его в графическую схему и убедитесь, что она остается сбалансированной.
В-пятых, практикуйтесь в использовании кругов Эйлера как можно чаще, решая разные типы задач. Со временем это станет для вас привычным и эффективным способом решения.
Следуя этим подсказкам и совершенствуя навык работы с диаграммами, вы значительно повысите свои шансы на успех в решении сложных логических задач с помощью замечательного инструмента - кругов Эйлера.
Часто задаваемые вопросы по применению кругов Эйлера
Метод кругов Эйлера вызывает много вопросов у тех, кто только начинает его осваивать. Давайте разберем самые популярные из них.
Вопрос: Можно ли использовать круги Эйлера в задачах без слов «некоторые», «часть» и других, задающих отношения между множествами?
Ответ: можно. Главное понимать, что круги Эйлера - это способ работы с множествами и отношениями между ними. Поэтому в любой задаче нужно выделить ключевые сущности или характеристики объектов, которые можно будет представить как отдельные множества.
Вопрос: А если в задаче речь идет об одном-единственном множестве, то применимы ли здесь круги Эйлера?
Ответ: в таком случае этот графический метод уже не так эффективен. Однако порой полезно рассмотреть заданное множество как объединение непересекающихся подмножеств по некоторому важному для решения признаку. Тогда опять же можно использовать диаграммы.
Вопрос: Как быть, если условие задачи слишком громоздкое и нарисовать диаграмму со всеми данными сложно или невозможно?
Ответ: в таком случае имеет смысл применить круги Эйлера не ко всей задаче целиком, а поэтапно - для визуализации промежуточных результатов или проверки гипотез. Главное понимать, где именно графическая интерпретация данных может помочь в решении.


























