В геометрии для изучения фигур используют две важные характеристики: длины сторон и углы между ними. В случае пространственных фигур к этим характеристиками добавляются двугранные углы. Рассмотрим, что это такое, а также опишем методику определения этих углов на примере пирамиды.
Понятие о двугранном угле
Каждый знает, что две пересекающиеся прямые образуют некоторый угол с вершиной в точке их пересечения. Этот угол можно измерить с помощью транспортира или воспользоваться тригонометрическими функциями для его вычисления. Образованный двумя прямыми угол называется линейным.
Теперь представим, что в трехмерном пространстве имеется две плоскости, которые пересекаются по прямой. Они изображена на рисунке.

Двугранным углом называется угол между двумя пересекающимися плоскостями. Так же как и линейный, он измеряется в градусах или радианах. Если к какой-либо точке прямой, по которой плоскости пересекаются, восстановить два перпендикуляра, лежащих в этих плоскостях, то угол между ними будет искомым двугранным. Определить этот угол проще всего, если воспользоваться уравнениями плоскостей в общем виде.
Уравнение плоскостей и формула для угла между ними
Уравнение любой плоскости в пространстве в общем виде записывается так:
A × x + B × y + C × z + D = 0.
Здесь x, y, z - это координаты точек, принадлежащих плоскости, коэффициенты A, B, C, D - некоторые известные числа. Удобство этого равенства для вычисления двугранных углов заключается в том, что оно в явном виде содержит координаты направляющего вектора плоскости. Будем обозначать его n¯. Тогда:
n¯ = (A; B; C).
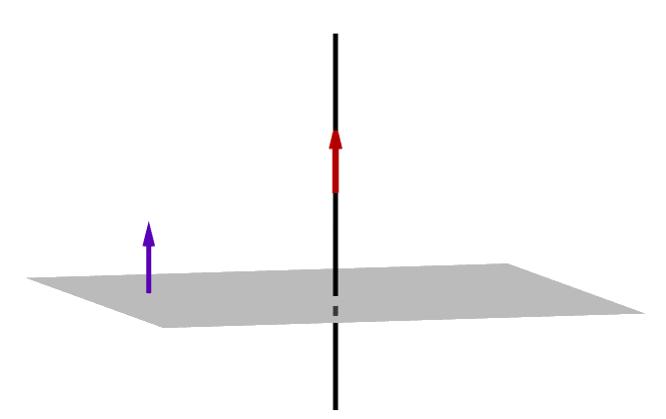
Вектор n¯ перпендикулярен плоскости. Угол между двумя плоскостями равен углу между их направляющими векторами n1¯ и n2¯. Из математики известно, что угол, образованный двумя векторами, однозначно определяется из их скалярного произведения. Это позволяет записать формулу для вычисления двугранного угла между двумя плоскостями:
φ = arccos (|(n1¯ × n2¯)| / (|n1¯| × |n2¯|)).
Если подставить координаты векторов, то формула запишется в явном виде:
φ = arccos (|A1 × A2 + B1 × B2 + C1 × C2| / (√(A12 + B12 + C12) × √(A22 + B22 + C22))).
Знак модуля в числителе используется, чтобы определить только острый угол, поскольку двугранный угол всегда меньше или равен 90o.
Пирамида и ее углы
Пирамидой называют фигуру, которая образована одним n-угольником и n треугольниками. Здесь n - целое число, равное количеству сторон многоугольника, который является основанием пирамиды. Данная пространственная фигура является многогранником или полиэдром, поскольку она состоит из плоских граней (сторон).
Двугранные углы многогранника-пирамиды могут быть двух типов:
- между основанием и боковой стороной (треугольником);
- между двумя боковыми сторонами.
Если рассматривается пирамида правильная, то названные углы для нее определить несложно. Для этого по координатам трех известных точек следует составить уравнение плоскостей, а затем воспользоваться приведенной в пункте выше формулой для угла φ.
Ниже приведем пример, в котором покажем, как найти двугранные углы при основании пирамиды четырехугольной правильной.
Четырехугольная правильная пирамида и угол при ее основании
Предположим, что дана правильная пирамида с квадратным основанием. Длина стороны квадрата равна a, высота фигура составляет h. Найдем угол между основанием пирамиды и ее боковой стороной.
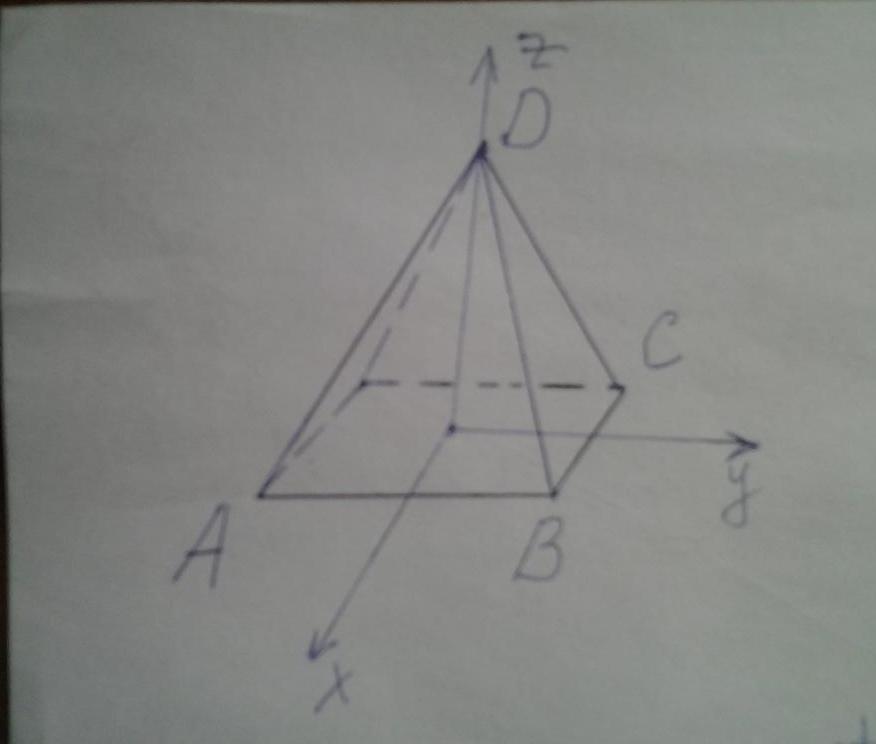
Поместим начало координатной системы в центр квадрата. Тогда координаты точек A, B, C, D, показанных на рисунке, будут равны:
A = (a/2; -a/2; 0);
B = (a/2; a/2; 0);
C = (-a/2; a/2; 0);
D = (0; 0; h).
Рассмотрим плоскости ACB и ADB. Очевидно, что направляющий вектор n1¯ для плоскости ACB будет равен:
n1¯ = (0; 0; 1).
Для определения направляющего вектора n2¯ плоскости ADB поступим следующим образом: найдем произвольные два вектора, которые ей принадлежат, например, AD¯ и AB¯, затем, вычислим их векторное произведение. Его результат даст координаты n2¯. Имеем:
AD¯ = D - A = (0; 0; h) - (a/2; -a/2; 0) = (-a/2; a/2; h);
AB¯ = B - A = (a/2; a/2; 0) - (a/2; -a/2; 0) = (0; a; 0);
n2¯ = [AD¯ × AB¯] = [(-a/2; a/2; h) × (0; a; 0)] = (-a × h; 0; -a2/2).
Поскольку умножение и деление вектора на число не изменяет его направления, то преобразуем полученный n2¯, разделив его координаты на -a, получим:
n2¯ = (h; 0; a/2).
Мы определили направляющие вектора n1¯ и n2¯ для плоскостей основания ACB и боковой стороны ADB. Остается воспользоваться формулой для угла φ:
φ = arccos (|(n1¯ × n2¯)| / (|n1¯| × |n2¯|)) = arccos (a / (2 × √h2 + a2/4)).
Преобразуем полученное выражение и перезапишем его так:
φ = arccos (a / √(a2 + 4 × h2)).
Мы получили формулу для двугранного угла при основании для правильной четырехугольной пирамиды. Зная высоту фигуры и длину ее стороны, можно рассчитать угол φ. Например, для пирамиды Хеопса, сторона основания которой составляет 230,4 метра, а начальная высота равнялась 146,5 метра, угол φ будет равен 51,8o.

Определить двугранный угол для четырехугольной правильной пирамиды также можно с помощью геометрического метода. Для этого достаточно рассмотреть прямоугольный треугольник, образованный высотой h, половиной длины основания a/2 и апофемой равнобедренного треугольника.


























